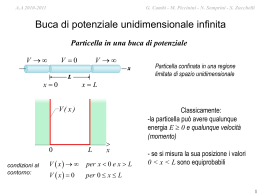
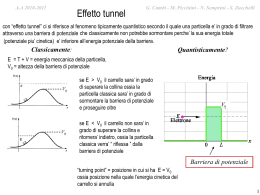
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Onde di materia
Se un’onda può comportarsi come un fascio di particelle, per simmetria, perché
una particella non dovrebbe comportarsi come un’onda? (De Broglie, 1924)
De Broglie propose di applicare a qualunque particella la relazione ipotizzata da
Einstein per i quanti di luce: p  h 
ad ogni particella di quantità di moto di modulo p è associata un’onda di
materia di lunghezza d’onda
h

p
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Proprieta’ ondulatorie della materia
•se gli elettroni fossero onde, si manifesterebbero proprieta’ diffrattive…
•
un esperimento chiave: diffrazione degli elettroni (Davisson & Germer 1927)
gli elettroni manifestano patterns di diffrazione
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
anche la materia è caratterizzata da una funzione d’onda con lunghezza d’onda,
frequenza, velocità, ampiezza
la funzione d’onda è denominata ampiezza di probabilità
 (r , t )
l’ipotesi di De Broglie è confermata sperimentalmente, anche a velocità
relativistiche, per es. con esperimenti di diffrazione di elettroni
Esempio numerico
a 300 m/s per un aeroplano (18000 kg) e un elettrone (9 ·10-31 kg):
aereo  1, 23 1040 m
elettro  2, 43 106 m
dato il valore molto piccolo della costante di Planck, un oggetto macroscopico si
comporta come una particella
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Comportamento ondulatorio della materia
tre esperimenti (quasi) virtuali:
1° esperimento: luce e interferenza
2° esperimento: pallottole e interferenza
3° esperimento: elettroni e interferenza
4
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
1° Esperimento: luce e interferenza
I ( )  I m cos 2  2  sin   
2
 2   d   sin 
   a   sin 
5
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
2° Esperimento: pallottole e interferenza ?
6
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
3° Esperimento: elettroni e interferenza !
7
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Analisi dei 3 esperimenti
ha senso chiedersi se un oggetto è un’onda o una particella?
parrebbe che:
• l’osservazione dell’oggetto determina la sua natura
ondulatoria o particellare
• simmetricamente a quanto visto per la radiazione
(onda EM/fotone), anche gli oggetti massivi
presentano carattere ondulatorio (elettroni che
interferiscono)
D

D
• e’ fondamentale il rapporto fra la  del sistema
osservato e le dimensioni dell’apparato di
osservazione (misura).
ha senso attribuire un carattere ondulatorio
anche alle particelle massive
8
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
la luce che passa attraverso una fenditura di dimensione D, mostra caratteri
ondulatori se   D (diffrazione); se << D è assimilabile ad un raggio (come una
particella).
nell’effetto Compton i raggi X si comportano come particelle, trasferendo impulso
ed energia (con  piccola rispetto alle dimensioni atomiche)
si tratta di aspetti (o descrizioni) diversi di uno stesso fenomeno.
ha senso attribuire un carattere particellare
anche alla radiazione elettromagnetica
9
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Analisi dei 3 esperimenti
Ad alta intensità sono evidenti le caratteristiche
dell’interferenza: vi sono massimi e minimi.
Le particelle non si cancellano; le onde sì!
ma anche riducendo di molto l’intensità (un fotone alla volta), la
distribuzione non cambia: nonostante si osservi una particella
(fotone) alla volta, la natura ondulatoria non si perde.
nelle zone dei massimi di intensità (densità) è maggiore la
probabilità che vada un fotone; ma, grande intensità (densità)
vuol dire grande (quadrato della) ampiezza dell’onda: quindi
la densità di probabilità di trovare una particella in un
certo punto è proporzionale al quadrato dell’ampiezza
dell’onda associata
P    E 2  
10
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
quindi, i campi elettrico e magnetico, oltre ad esercitare forze sulle cariche misurano la
probabilità di trovare in un punto la particella associata (fotone)
inoltre:
quando una grandezza ha natura ondulatoria, vi è una qualche incertezza in alcune
delle sue proprietà particellari.
la diffrazione di un’onda piana attraverso una fenditura è tanto
più accentuata quanto più essa è stretta in rapporto alla
lunghezza d’onda:
 sin  
I  I m 

  
2


2


x sin 

quanto più stringiamo la posizione in x, (x  0) tanto più
abbiamo una dispersione della quantità di moto px nella direzione x
(principio di indeterminazione)
x px  Cost
11