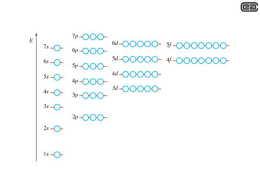
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
Eq. di Schrödinger - indipendente dal tempo - in coordinate polari sferiche

2
  (r )  U (r ) (r )  E (r )  
2
2
2m
 x  r sin  cos 

 y  r sin  sin 
 z  r cos 

2m
 2 (r , ,  )  U (r ) (r , ,  )  E  (r , ,  )
2
2
2
1  2  1 1  
 
1 2 
  2  2  2  2 r
 2
sin 
 2




x y z
r r  r  r  sin   
  sin   2 
2
le variabili angolari compaiono solo in un termine percio’ ricerco le soluzioni nella forma:
 (r , ,  )  R(r )Y ( ,  )
1  2 


1 2
 1 1  

  2 r
R(r )Y ( ,  )   2 
R
(
r
)
Y
(

,

)
   U (r ) R(r )Y ( ,  )  E R(r )Y ( ,  )
 sin  R(r )Y ( ,  )   2
2
2m  r r  r
r
sin





sin








2
 Y ( ,  )   2 


R( r )  2
 R( r )  

ossia 
r
R
(
r
)

sin

Y
(

,

)

Y
(

,

)

  (U (r )  E )R(r )Y (,  )  0

 2

 2 2
2
2m  r 2 r  r
r
sin





r
sin







2
dividendo per
R(r )Y ( ,  )
e moltiplicando per 
2mr 2
2
si ottiene :
 1  2 
 2mr 2
1
 

1
2


R(r )  
Y ( ,  )   2 (U (r )  E )  0

r
 sin  Y ( ,  )  
2
2
R
(
r
)

r

r
Y
(

,

)sin





Y
(

,

)sin









A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
2
 1  2 

1  1 
Y ( ,  )
1  2Y ( ,  ) 
 2mr
r
R
(
r
)

(
U
(
r
)

E
)

(sin

)



0


2
2
2
R
(
r
)

r

r
Y
(

,

)
sin





sin









riarrangiando i termini: 
dato che il primo termine, che dipende solo da r, e’ indipendente dal secondo, che dipende solamente da  e  , affinche’ l’equazione
sia sempre verificata bisogna che i due termini siano entrambi costanti, posto che la costante valga l(l+1) , dove l e’ un intero, si dovra’ avere
2
 1  2 

 2mr
r
R
(
r
)

(U (r )  E )   l (l  1)



2

 R(r ) r  r

e
 1 
Y ( ,  )
1  2Y ( ,  ) 
(sin 
) 2

  l (l  1)
Y ( ,  )  sin  

sin   2 
1
parte radiale
parte angolare

Y ( ,  )  2Y ( ,  )
(sin 
)
 l (l  1)Y ( ,  ) sin 2 
per quanto riguarda la parte angolare si ha: sin 
2



tenteremo di nuovo di operare sulla parte angolare separando le variabili,
del tipo Y ( ,  )  G ( ) F ( )
dividendo per
sostituendo si ottiene
G( ) F ( ) si ha
ossia ipotizzando una soluzione

G( ) F ( )  2G( ) F ( )
sin  (sin 
)
 l (l  1)G( ) F ( ) sin 2   0
2



1

G( )
1  2 F ( )
2
sin  (sin 
)  l (l  1)sin  
0
G( )


F ( )  2
poiche il primo termine, che dipende solo da , e’ indipendente dal secondo, che dipende solamente da , sara’ possibile utilizzare
le derivate normali: quindi
1 
d
dG( ) 
1 d 2 F ( )
2
)   l (l  1)sin  
0
 sin  (sin 
G( ) 
d
d 
F ( ) d 2
affinche’ l’equazione sia sempre verificata bisogna che i due termini siano entrambi costanti,
dove m e’ un intero, si dovra’ avere
1 
d
dG ( ) 
(sin 
)   l (l  1)sin 2   m 2
 sin 
G ( ) 
d
d 
e posto che la costante assuma il valore m2 ,
e
d 2 F ( )
 m2
2
F ( ) d
1
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
d F ( )
 m2 F ( )
2
d
2
le soluzioni dell’equazione
sono
F ( )  Aeim
e
F ( )  Aeim
ma di solito si ingloba la costante come fattore moltiplicativo nella funzione G () e sempre per convenzione si assume come soluzione
F ( )  eim consentendo poi ad m di assumere anche valori negativi
dato che l’angolo azimutale  ha periodicita’ di 2p e dato che
dopo un avanzamento di 2p si torna allo stesso punto dello spazio imporremo la condizione che
ossia
e
im (  2p )
e
im
vale a dire
m  0,  1,  2, ....
nello specifico
e
im 2p
1
F (  2p )  F ( )
cio’ comporta che il numero quantico m debba in effetti essere un intero
e, limitandosi a questo contesto, m non avrebbe limite superiore
nota bene: questa non e’ una supposizione scontata a priori infatti esistono grandezze fisiche che non ritornano nella stessa identica
condizione dopo una rotazione di 360 gradi. Es. spinori o come esempio classico il cameriere ed il piatto che ruota
id
quindi per essere corretti occorrerebbe moltiplicare per una fase tipo e id ossia affermare che F (  2p )  e F ( )
le soluzioni a
1 
d
dG ( ) 
(sin 
)   l (l  1)sin 2   m 2 ossia della
 sin 
G ( ) 
d
d 
sin 
d
dG ( )
(sin 
)  (l (l  1)sin 2   m2 )G ( )  0
d
d
m
sono G ( )  APl (cos  )
m
dove i
Plm sono
le funzioni associate di Legendre definite come Pl ( x)  (1  x )
m
2
2
m
d Pl ( x)
dx
m
1 d l ( x 2  1)l
mentre i Pl(x) sono i polinomi di Legendre che e’ consuetudine definire, usando la formula di Rodrigues, come Pl ( x)  l
2 l!
dxl
da notare come :
• affinche’ la formulazione dei polinomi di Legendre nella forma di Rodrigues abbia senso il numero
quantico l deve essere un numero intero positivo o nullo quindi l  0, 1, 2, ...
• dalla definizione delle funzioni associate di Legendre risulta che deve essere m intero ed |m| ≤ l quindi
per ogni valore assegnato di l sono possibili ( 2l+1) valori per m con m  l , (l +1),..  1, 0,  1, ... (+l  1), l
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
Parte radiale
2
 1  2 

 2mr
r
R
(
r
)

(
U
(
r
)

E
)

  l (l  1)


2

 R(r ) r  r

d  2 dR(r )  2mr 2
r
  2 (U (r )  E )  l (l  1)
R(r ) dr 
dr 
1
dove si e’passati dalle derivate parziali a quelle normali visto che R dipende solo dalla variabile radiale r
o anche, riarrangiando i termini :
d  2 dR(r )  2mr 2
r
  2 (U (r )  E ) R(r )  l (l  1) R(r )
dr 
dr 
u (r )  rR(r )
equazione che puo’ essere semplificata se poniamo:
da questa condizione ne deriva che R (r ) 
dR(r )

dr
u (r )
r
du (r )
dr  1 (r du (r )  u (r ))
2
r2
dr
r
e applicando regola di derivazione del prodotto di funzioni otteniamo
u (r )  r
inoltre
d 2 dR(r )
d
1 du (r )
d du
d du (r ) du (r ) du (r )
d 2u (r ) du (r ) d 2u (r )
(r
)  (r 2 ( 2 (r
 u (r )))  (r  u (r ))  (r
)
r

r

dr
dr
dr
r
dr
dr dr
dr
dr
dr
dr 2
dr
dr 2
dr
dunque la
ossia
d  2 dR(r )  2mr 2
r
  2 (U (r )  E ) R(r )  l (l  1) R(r )
dr 
dr 
d 2u (r ) 2mr 2
u (r )
u(r )

(
U
(
r
)

E
)

l
(
l

1)
2
2
2
2
diviene
d 2u (r ) 2mr 2
u (r )
u (r )
r

(
U
(
r
)

E
)

l
(
l

1)
2
dr 2
r
r
infine, semplificando il termine
r2
d 2 u ( r ) 2m
u (r )

(
U
(
r
)

E
)
u
(
r
)

l
(
l

1)
2
2
2
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
2
d 2u ( r ) 
l (l  1) 

U
(
r
)

e, riarrangiando i termini si ottiene la 

 u (r )  E u (r )
2
2m dr 2
2
m
r


2
equazione che diviene equivalente alla equazione di Shroedinger indipendente dal tempo in una dimensione
ossia alla
dove
d 2

 V  E 
2m dr 2
2
l (l  1)
2m r 2
2
l (l  1)
e’ detto centrifugo in quanto tende ad allontanare dall’origine del centro di forza
2
2m r
Veff  U (r ) 
il termine
a patto di sostituire al potenziale V un potenziale efficace Veff
2
Atomo idrogenoide : potenziale coulombiano
le soluzioni all’equazione

 1 d 2 dR(r ) l (l  1)
(r
)

2m  r 2 dr
dr
r2
2
2

e2
R(r )  
R(r )  ER(r )
4
p
r

o
sono i polinomi di Laguerre: come conseguenza affinche’ si abbia convergenza dei polinomi di Laguerre
il numero quantico l puo’ assumere al massimo il valore n-1
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
quindi per un generico valore del numero quantico n
l  0, 1, 2, ... (n  1)
il numero quantico l puo’ assumere gli n valori
ma per ciascun valore di l vi sono
2l 1 valori possibili per il numero quantico m
n 1
e la degenerazione di un livello energetico En associato al numero quantico n sara’ pari a
quindi
E1  degenerazione = 1
n  1, l  0, m  0
E2

degenerazione = 4
 (2l  1)  n
l 0
E3  degenerazione = 9
n  2, l  0, m  0
n  3, l  0, m  0
n  2, l  1, m  1
n  3, l  1, m  1
n  2, l  1, m  0
n  3, l  1, m  0
n  2, l  1, m  1
n  3, l  1, m  1
n  3, l  2, m  2
n  3, l  2, m  1
n  3, l  2, m  0
tenuto conto dello spin degli elettroni e del principio di esclusione di Pauli cio’
spiega la capienza in elettroni dei vari livelli energetici dell’atomo idrogenoide
E1

degenerazione = 1

numero di elettroni possibili = 2
E2

degenerazione = 4

numero di elettroni possibili = 8
E3

degenerazione = 9

numero di elettroni possibili = 18
n  3, l  2, m  1
n  3, l  2, m  2
2
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
in conclusione
le funzioni d’onda dell’atomo di idrogeno, propriamente normalizzate, sono
r
 2  (n  l  1)!  na  2r  2l 1  2r  m
 n ,l , m ( r ,  ,  )   
e   Ln l 1   Yl ( ,  )
3
na
2
n
((
n

l
)!)
 
 na 
 na 
3
dove gliL
p
q p
dp
( x)  (1)
Lq ( x)
p
dx
p
l
sono i polinomi associati di Laguerre
d q x q
(e x ) sono i polinomi di Laguerre
e Lq ( x)  e
q
dx
x
le
Yl m ( ,  )
4p 0 2
ed a 
me2
sono le armoniche sferiche
e’ il raggio di Bohr
a  0.529 10 10 m
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
partendo soltanto dalla degenerazioni dei livelli energetici e dal principio di esclusione di Pauli
si puo’ tentare di costruire la tavola periodica degli elementi
idrogeno
1 elettrone
n=1
l=0
m=0
s = -1/2
elio
2 elettroni
n=1
n=1
l=0
l=0
m=0
m=0
s = -1/2
s = +1/2
3 elettroni
n=1
n=1
n=2
l=0
l=0
l=0
m=0
m=0
m=0
s = -1/2
s = +1/2
s = +1/2
litio
ma se n = 2 sia l = 0 che l =1 sono stati possibili ed hanno la stessa energia
quindi perche’ non occupare prima lo stato con l = 1 ? la risposta e’ che non si puo’ ignorare la repulsione
coulombiana tra gli elettroni
la presenza del termine centrifugo fa si’ che il valore del raggio medio ad n fissato aumenti in funzione del
numero quantico l o, detto in altri termini, fa si’ che gli elettroni tendano in media ad allontanarsi
maggiormente dal centro di forza all’aumentare del numero quantico l a parita’ di numero quantico n
piu’ lontano dal nucleo e’ l’elettrone piu’ assume rilevanza l’effetto di schermatura o “screening” degli
elettroni piu’ interni che fa si’ che piu’ e’ lontano l’elettrone minore carica efficace percepisce
dunque tenendo conto della repulsione degli elettroni lo stato con l = 0 e’ quello piu’ strettamente legato al
nucleo, ossia e’ quello che ha l’energia minore e l’energia, a parita’ di n, aumenta all’aumentare di l
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli
Determinare nell’atomo di idrogeno quale sia il valore piu’ probabile di r negli stati
caratterizzati dai numeri quantici n e dal massimo numero quantico orbitale possibile
nell’ atomo di idrogeno P(r) e’ la densita’ di probabilita’ radiale ossia P(r)dr e’ la probabilita’ di trovare
l’elettrone ad una distanza compresa tra r e r + dr dal nucleo.
il numero quantico l puo’ assumere al massimo valore n-1, quindi lmax= n - 1
Rn ,l  n 1  r e
l

r
na
r
n 1
e

r
na
o


a 2 
 0.529 A
2
c
me c
dove
e’ il raggio di Bohr e  e’ la “massa ridotta” del sistema protone elettrone

u
R
r
e
 u  rR
me m p
me  m p

me
m
 me (1  e )  me
me
mp
1
mp
n 1
u  r r e

r
na
r e
n

r
na
Prob(r  [r,r  dr])  un2,l  n 1  r 2 n e

quindi
2r
na
un ,l  n 1  r n e

r
na
A.A 2010-2011
G. Cambi - M. Piccinini - N. Semprini - S. Zucchelli

P
dP d 2 n  na
2 2 n  na
2 n 1
na

 (r e )  2nr e  r e  0
r
dr dr
na
2r
raccogliendo a fattor comune
2r
2r
2 n 1
ed
2r
e

2r
na
si ha
2r
2 n 1
e

2r
na
1
r0
escludendo le soluzioni a zero e all’ infinito resta da risolvere la n 
na
equazione che ha per soluzione :
1
(n  r )  0
na
r  n2a
la probabilita’ e’ massima in corrispondenza di quegli rn tali per cui :
ossia in corrispondenza delle orbite dell’atomo di Borh
rn  n 2 a