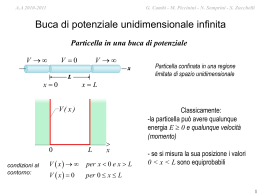
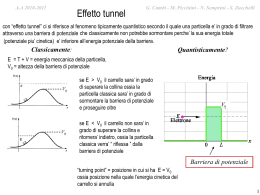
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Continuità della funzione d’onda
una funzione appartiene a C0 se e’ continua ovunque sul dominio di esistenza
una funzione appartiene a C1 se e’ continua e derivabile ovunque e se ha derivata prima continua
ovunque sul dominio di esistenza, etc.
riscrivendo l’equazione di Schrödinger nella forma:
d 2y ( x) 2m
 2 (V ( x)y ( x)  Ey ( x))
2
dx
se ne deduce che se V(x) è una funzione Cn , allora
y(x)
deve essere una funzione Cn+2
in generale:
• se V(x) è una funzione continua,
y''(x) e y '(x) sono continue e y(x) è una funzione C2
• se V(x) presenta un salto finito, allora la
continua e così anche la
y(x)
y ''(x) sarà discontinua, ma la y '(x) sarà
• se V(x) presenta un salto infinito, allora la y ''(x) sarà discontinua, e così anche la
ma si puo’ dimostrare che la
y(x) sarà
regola generale: la
y’(x),
ancora continua
y(x)
è sempre continua
1
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Buca di potenziale finita
V( x )
0
x
II
I
V(x) = –V0 per 0 > x > L
V(x) = 0 per |x| > L
III
V0
 e  x continue
nei punti di discontinuità di V
0
L
per risolvere il problema occorre calcolare e raccordare fra di loro le soluzioni stazionarie per …
 2y

 Vy  Ey
2
2m x
2
… 3 regioni spaziali …
 I

 II

 III
V0  E  0
E0
… e ....
2 regioni energetiche

un totale di 6 soluzioni
2
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Buca di potenziale unidimensionale finita
funzione d’onda dello stato fondamentale per un potenziale dato da:
x  0 (I )
 0

V ( x)  V0 0  x  L ( II )
 0
x  L ( III )

V(x)
I
II
0
III
L
x
il sistema sarà caratterizzato da “stati liberi” e da “stati legati”
gli stati liberi si hanno se E > 0 e saranno assimilabili ad onde piane quando Vo 0,
gli stati legati si hanno se E < 0 e saranno simili a quelli della buca di potenziale infinita per Vo ∞
iniziando dagli stati legati nella regione
di modo che
kR

quindi
I (x < 0) si ha
V(x) = 0
E < 0 porremo k  
2mE
2
d 2y ( x)
2mE
kx
 kx


y
(
x
)

y
(
x
)

Ce

De
2
dx 2
se x e’ negativo ekx diverge per x -∞ dunque questa soluzione non sarebbe normalizzabile percio’ si
dovra’ imporrre che D = 0
quindi
d 2y ( x)
2mE
kx


y
(
x
)

y
(
x
)

Ce
2
dx 2
3
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
un analogo ragionamento si potra fare per la regione x > L mentre per la regione 0 < x < L ipotizziamo
esistano soluzioni tipo buca di potenziale infinita in conclusione cercheremo soluzioni del tipo :
2mE

Ce  kx
x  0 (I )
nelle regioni I e III
con k   2

y ( x)   Asen(k ' x)  Bcos(k ' x) 0  x  L ( II )
2m(V0  E )
 kx

nella regione II
con
k
'

Ge
x

L
(
III
)
2

essendo E negativa si avra’ che k e’ reale positivo da notare poi come pur essendo E negativa essa
debba essere maggiore di –V0 o la funzione d’onda all’interno della buca non potrebbe essere normalizzata
quindi E + V0 > 0 e di conseguenza anche k’ e’ reale positivo
imponendo la continuità di
ψ e di ψ' in 0 e in L
y I (0)  y II (0)  C  B
y I (0)  y II (0)  Ck  k ' A
y II ( L)  y III ( L)  A sin(k ' L)  B cos(k ' L)  Ge  kL
fisso A e B
fisso G
 ( L)  Ak 'cos(k ' L)  k ' B sin( k ' L)  kGe  kL
y II ( L)  y III
sostituendo e riarrangiando i termini: 2cot (k ' L) 
k' k

ossia una relazione di quantizzazione
k k'
4
A.A
A.A.2010-2011
2009-2010
Buca di potenziale finita
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
notare le differenze tra la
buca di potenziale finita
(sinistra), l’analogo classico e
la buca a potenziale infinito
(destra).
in questo caso, la particella NON è confinata nella buca, ma può essere trovata anche
nelle regioni I e III, non permesse classicamente, effetto tunnel
lunghezza di penetrazione della barriera
δ: ψ(x) = e-αx

1


2m(V  E )
5
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Stati liberi e stati legati in meccanica quantistica
Stati liberi: la particella può essere ovunque nello spazio
caratteristiche generali degli stati liberi in Meccanica Quantistica:
- assenza di onde stazionarie
- assenza di quantizzazione
Stati legati: la particella è confinata in una zona finita di spazio .... cum grano salis .
dato che un particella puo’ “ filtrare” attraverso qualsiasi barriera di potenziale finita
nota: la distinzione tra stati legati e stati liberi in realta’ e’ molto semplice in meccanica
quantistica proprio grazie all’effetto tunnel: dato che un particella puo’ “ filtrare” attraverso
una qualsiasi barriera di potenziale finita e quindi puo’ venirsi comunque a trovare in un
punto qualunque dello spazio, cio’ che conta e’ l’andamento del potenziale all’infinito rispetto
all’energia totale E
se
se
E  V ()
E  V ()
e (and)
o (or)
E  V ()
E  V ()
si ha uno stato legato
si ha uno stato libero o di “scattering”
dato poi che la maggior parte dei potenziali di interesse fisico vanno a zero all’infinito il
criterio si semplifica ulteriormente in
se
E0
se
E  0 si ha uno stato libero o di “scattering”
si ha uno stato legato
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Buca di potenziale finita
Stati legati: –V0 < E < 0
0
L
L
 k '2 y
k'
y ( x)  Ce x
y
  Ce x
x
y ( x)  A sin  k ' x   B cos  k ' x 
y ( x)  Ge x
y
 k '  A cos  k ' x   B sin  k ' x  
x
y
  Ge  x
x
http://www.quantum-physics.polytechnique.fr/
Sez. 2.3
7
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Buca di potenziale finita
Stati di diffusione: E > 0
0
L
L
 k '2 y
k'
y ( x)  Aeikx  Beikx y ( x)  C sin  k ' x   D cos  k ' x 
y ( x)  Geikx
y
y
 ik  Aeikx  Be  ikx 
 k ' C cos  k ' x   D sin  k ' x  
x
x
y
 ikGeikx
x
8
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Stati di diffusione :
sorgente di elettroni, posta a sinistra dell’origine, nel caso della presenza di una buca di
potenziale tra x = 0 e x = L
II
III
V(x)
x  0 (I )
 0

V ( x)  V0 0  x  L ( II )
 0
x  L ( III )

I
L
0
x
il fascio di elettroni viaggia da sinistra, (dalla regione I ), verso destra, (verso la regione III) e nella
regione II incontra la buca di potenziale
nella regione I dove V = 0 , il fascio incidente di elettroni e’ assimilabile ad un’onda piana
progressiva quindi sara’ descrivibile come
Ae  i ( kx t )
 prevedendo che a causa della presenza del potenziale possa avvenire riflessione teniamo in
conto che nella regione I vi possa essere anche un’onda piana riflessa all’indietro
l’onda riflessa viaggia nello stesso mezzo dell’onda incidente e ne avra’ le stesse caratteristiche
a parte l’ampiezza, quindi si potra’ scrivere
Bei (  kxt )
nella regione I potrebbero quindi essere presenti due onde e la funzione d’onda in quella
regione sara’
( x, t )  Aei ( kx t )  Bei (  kx t )
k  2mE /
9
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
nella regione II si puo’ fare un ragionamento del tutto identico salvo che in questa regione bisognera’
tener conto della presenza del potenziale V0 e quindi potranno cambiare ampiezze e numeri d’onda
, quindi nella regione II si ha
( x, t )  Cei ( k x t )  Dei (  k x t )
k   2m( E  V0 ) /
infine nella terza regione se vi e’ una onda sara’ di tipo progressivo dato che di nuovo V = 0 con energia
e numero d’onda uguali a quella che si avevano nella regione I
in conclusione le soluzioni ad E fissata sono:
 Ae i ( kx t )  Be i (  kx t )
x  0 (I )
k  2mE /
  i ( k x t )
 i (  k x t )
 ( x, t )  Ce
 De
0  x  L ( II ) con
k   2m( E  V0 ) /
 i ( kx t )

Fe
x  L ( III )

condizioni al contorno in 0 e in L  4 relazioni: fisso B,C,D,F piu’ la condizione di normalizzazione di 
non ho alcuna relazione di quantizzazione !
si definisce:
in generale R ≠ 0
probabilità di riflessione
R  B / A  f1 (k , L,V0 )
probabilità di trasmissione
T  F / A  f 2 (k , L,V0 )
2
2
2
2
Analogia classica: un tombino aperto in mezzo al marciapiede: se si e’ distratti ci si puo’ cadere dentro e restare intrappolati ( stato legato)
Ma si puo’ essere anche distratti e fortunati e inciampare solamente sul bordo del tombino e riuscire poi a continuare a camminare. Scattering e stato libero
Ma non vi aspettreste mai di inciampare ed essere riflessi all’indietro dal tombino!
10
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
In generale:
1. Le equazioni di raccordo nei punti di discontinuità, più quelle di normalizzazione, permettono di
calcolare le varie costanti e trovare gli stati stazionari.
2. Gli stati legati sono in numero finito (energia quantizzata), dipendente dalla profondità della
buca.
3. Gli stati di diffusione invece non sono quantizzati: ogni energia è consentita.
4. Gli stati legati “debordano” nelle zone con V > V0 , dove vi è una probabilità di presenza della
particella diversa da zero (
5. Una particella incidente sulla buca (da sinistra) con E > 0 può essere trasmessa
(e questo è
il solo possibile risultato classico), ma può anche essere riflessa.
Esempio: andamento di y n ( x )
per una buca di potenziale con
V0  30 eV; 2a  100 pm
in questo caso sono possibili solo i
tre stati quantici caratterizzati da
n=1, 2, 3.
2
11
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Buche di potenziale
Assorbimento / Emissione
cosa succede se all’elettrone viene fornita energia ?
esso può passare ad un livello di energia superiore, che però
non può che essere uno di quelli corrispondenti ad un valore di
energia permesso, in base alla relazione:
 h2  2
En  
n
2 
 8mL 
N.B.: diminuendo L, En aumenta, a parità di n
l’elettrone può quindi assorbire solo valori discreti di energia:
E  Esup  Einf
dove Esup ed Einf debbono essere una coppia di valori definiti da
 h2  2
En  
n
2 
 8mL 
12
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Buche di potenziale
Assorbimento / Emissione
Un modo possibile per l’elettrone di assorbire l’energia per “saltare” ad un livello più alto
(salto quantico) di quello in cui si trova consiste nel ricevere un fotone.
deve però essere verificata esattamente la relazione:
h  E  Esup  Einf
relazione che vale sia per l’assorbimento che per l’emissione di fotoni
una volta raggiunto il livello superiore (eccitato) l’elettrone tenderà a riportarsi a valori
inferiori (purché possibili) di energia.
durante tale transizione vengono emessi uno o più fotoni:
13
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Buche di potenziale
Trappole elettroniche a più dimensioni
se un elettrone è intrappolato in una trappola a due (recinto rettangolare) o tre dimensioni (scatola
retta), si arriva alle seguenti relazioni per l’energia che può avere l’elettrone:
2
2


n
h nx
y

 2  2 
8m  Lx Ly 
2
Enx ,ny
2
2
2 

n
h nx
n
y

 2  2  z2 
8m  Lx Ly Lz 
2
Enx ,ny ,nz
sono numeri
nx , n y , nz quantici.
in generale, stati differenti, cioè con diversi numeri
quantici, hanno energie diverse. Per alcune situazioni
ciò non è vero e gli stati corrispondenti sono detti
degeneri.
vai all’esercizio  densita’ degli stati in una buca tridimensionale
14
A.A
A.A.2010-2011
2009-2010
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
Trappole elettroniche a più dimensioni
si possono costruire trappole artificiali per elettroni; tra esse si citano in letteratura:
• i punti quantici
• i recinti quantici
• le nanocristalliti
Wikipedia: Un punto quantico (dall'inglese quantum dot) è una nanostruttura formata da un'inclusione di un materiale
semiconduttore, con una certa banda proibita e con dimensioni tipiche comparabili alla lunghezza d'onda di De Broglie,
all'interno di un altro semiconduttore con banda proibita più grande.
Tale struttura genera un pozzo di potenziale tridimensionale che confina i portatori di carica (elettroni e lacune) in una
piccola regione di spazio in cui i livelli energetici divengono discreti. Quest'ultima proprietà ha portato all'associazione tra
punti quantici ed atomi generando lo pseudonimo "atomi artificiali".
Tra i possibili impieghi, vi sono l'implementazione dei qbit necessari per un computer quantistico, e lo studio dello stato di
condensato di Bose - Einstein. Un altro possibile impiego è quello di riserva di energia, di sorgente luminosa o per la
produzione a basso costo di celle fotovoltaiche.
15
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Buche di potenziale
l’atomo di idrogeno
q1 q2
1 e2
U

4 0 r
4 0 r
1
la buca di potenziale (tridimensionale) in cui
si trova confinato l’elettrone dell’atomo di
idrogeno:
le funzioni d’onda che descrivono gli stati quantici
discreti dell’atomo di idrogeno e le corrispondenti
energie quantizzate si trovano risolvendo l’equazione di
Schroedinger tridimensionale
 2
2
2

 2 2 2
2m  x
y
z
2



(
r
,
t
)

U
(
r
)

(
r
,
t
)

i
(r , t )

t

16
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
l’atomo di idrogeno
 me4
En   
2
8

h
0

 1 R 13.6
eV
 2  2 
2
n
n
n
Il livello fondamentale (energia minima)
dell’elettrone si ha per n=1 e vale -13.6 eV.
Il livello fondamentale e quelli relativi ai valori di n
fino a 6 sono riportati a lato
Per n   si ottiene
stato non quantizzato.
En  0 cioè uno
L’elettrone tende a restare nel suo stato
fondamentale. Può passare ad uno stato eccitato
solo assorbendo energia ad esempio un fotone di
E  h
energia
esattamente pari alla differenza dei valori di energia
dei due livelli
 1
1 
E  R  2  2 
 n f ni 


17