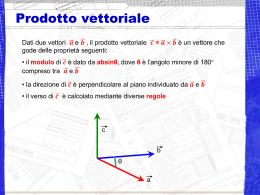
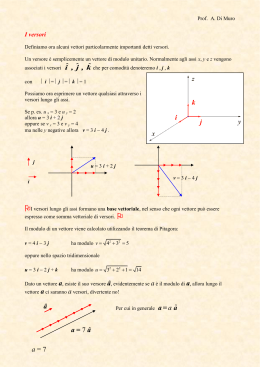
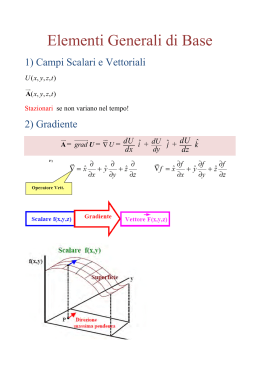
Corso di Fisica 3
Prof. R. Pizzoferrato
Università di Roma Tor Vergata
CCS Meccatronica – Colleferro - A.A. 2006/07
Possibili testi di riferimento:
S. Focardi, I. Massa, A. Uguzzoni “Fisica Generale –
Elettromagnetismo” Casa Editrice Ambrosiana
Serway, Beichner “Fisica Vol. II” EdiSES
D. Halliday, R. Resnick, J. Walker “ Fondamenti di
Fisica -Elettrologia, Magnetismo, Ottica” Casa Editrice
Ambrosiana
P. Mazzoldi, M. Nigro, C. Voci “Elementi di Fisica:
Elettromagnetismo” EdiSES
Cap. 1 Strumenti matematici
Analisi matematica e vettoriale
x2
dF(x)
dx
 F(x)
dx
x1
Vettori
^
k
z
y
x
^
i
v
v = vx ^
i + vy^j+ vz^k
v  ( v x , v y , v z)
^
j
Coseni direttori
vx =|v| Cos x ; vy =|v| Cos  y ; vx =|v| Cos  z
v 
v 2x  v 2y  v 2z
Calcolo differenziale vettoriale
dv
a
dt
dv x
ax 
dt
dv y
ay 
dt
dv z
az 
dt
t2
v x   ax dt
t2
v   a dt
t1
t1
t2
v y   a y dt
t1
t2
v z   a z dt
t1
Prodotto scalare
A  ( Ax , Ay , Az)
vettori
B  ( Bx , By , Bz)
scalare
A  B  Ax Bx  Ay By  Az Bz
A  B  A B Cos( A^B )
Prodotto vettoriale
vettori
A  B  ( A  B) x ˆi  ( A  B) y ˆj  ( A  B) z kˆ
vettori
( A  B) x  Ay Bz  Az By
( A  B) y  Az Bx  Ax Bz
( A  B) z  Ax By  Ay Bx
^
i
A B  Det
^
j
^
k
Ax Ay
Az
Bx By
Bz
A  B  A B Sin ( A^ B )
AxB
Verso di AxB ?
Regola mano destra
B
 ^
AB
A
AxB =
- BxA
CAMPO DI UN VETTORE
v  v(r)  v( x, y, z)
^
k
^
i
Campo vettoriale uniforme v = cost.
^j
Campo vettoriale non uniforme:
Campo vettoriale non uniforme:
CAMPO DI UN VETTORE
v  v(r)  v( x, y, z)
Campo vettoriale non uniforme
LINEE DI FORZA DEL CAMPO
In ogni punto hanno il vettore come tangente
Angolo solido sotteso da cono con base
retta
Base area A1
 = A1 / r12
(Steradianti)
 = A 2 / r2 2
Altezza r1
Base area A2
O
Altezza r2
Angolo solido: si può immaginare come apertura
angolare “tridimensionale “ sottesa dalla base retta
del cono al suo vertice
Angolo solido non dipende dalla distanza r a cui si
trova la base retta intercettata.
Angolo solido sotteso da cono con base
non retta
Base retta
area A =A’ Cos 
A
 = A / r2
(Steradianti)
O
Altezza r
Base area A’

Angolo solido sotteso da una sfera al
centro
dS
r
d
C
d = dS /r2
Sommando contributi di tutti
elementari identici di altezza  r
1
Centro  2
r
4r
dS  2  4

r
A sfera
2
i
coni
Flusso di un vettore
Area S
v
dS
d  v cos θ dS d  v ndS
^
 tot   v  ndS
^
S
Flusso di un vettore
d  v cos θ dS d  v ndS
^
 tot   v  ndS
^
S
Significato del flusso di v
Quando v rappresenta campo di velocità di
particelle di un fluido
^
n
Area S

dS
v
Φ( v)   v  n dS
^
S
Il flusso di v attraverso area S
rappresenta il volume di fluido che fluisce
attraverso S nell’unità di tempo.
Caso particolare (importante)
Se il vettore v è uniforme su tutta la
superficie :
tot   v  nˆ dS  v cos  dS  v cos  S
S
S
Se inoltre v è anche perpendicolare alla
superficie:
 tot   v  nˆ dS  v  dS  v S
S
S
Integrale di linea di un vettore
v

dl

dL  v  dl  v dl cos θ
L
v

d
l


Ad esempio: se il campo vettoriale è una forza
l’integrale di linea è il lavoro della forza lungo
il percorso .
Caso particolare (importante)
Se la proiezione del il vettore v sulla
tangente a  è costante su tutto il
percorso:
v

dl
L


dl
dl

dl

v

d
l

v

d
l

v

l

cos





Circuitazione di un vettore
v
dl 

dC  v  dl  v dl cos θ
C  v  dl
Γ
E’ l’integrale di linea lungo una
linea chiusa
Circuitazione di un vettore
v
dl 

dC  v  dl  v dl cos θ
C  v  dl
Γ
Se il campo vettoriale è una forza la
circuitazione è il lavoro della forza lungo un
percorso chiuso.
Se il campo vettoriale è conservativo C = 0