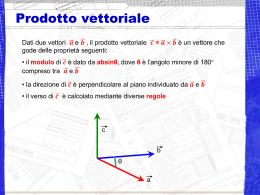
A08
Paolo Podio-Guidugli
Lezioni di Statica
Copyright © MMXIV
ARACNE editrice int.le S.r.l.
www.aracneeditrice.it
[email protected]
via Raffaele Garofalo, 133/A–B
00173 Roma
(06) 93781065
isbn
978–88–548–7503–6
I diritti di traduzione, di memorizzazione elettronica,
di riproduzione e di adattamento anche parziale,
con qualsiasi mezzo, sono riservati per tutti i Paesi.
Non sono assolutamente consentite le fotocopie
senza il permesso scritto dell’Editore.
I edizione: settembre 2014
Presentazione
La Statica è la parte più antica e basilare della Meccanica: questo libretto ne
contiene un’esposizione mirata a fornire agli studenti di ingegneria gli strumenti
indispensabili a trattarne gli argomenti che sono prodromo indispensabile di quelli
trattati nei corsi di Scienza delle Costruzioni.
La prima redazione era nient’altro che la collezione delle tracce manoscritte
delle mie lezioni, messe in rete per gli studenti di Meccanica dei Solidi dell’anno
accademico 2002-2003 (la denominazione Meccanica Razionale, ancorché coniata
da Newton, era appena stata rottamata, a significare uno dei primi raggiungimenti
della ‘rivoluzione del 3+2’). A quella raccolta di lezioni aveva fatto seguito l’anno
dopo, con identiche modalità e fini, quella delle tracce per le lezioni di Scienza delle
Costruzioni (questa denominazione, cosı̀ intraducibilmente italiana, si era subito
rivelata più difficile da rottamare). Poichè presso l’allora inconsapevole di futura
rottamazione Facoltà di Ingegneria dell’Università di Roma TorVergata l’anno
accademico aveva assunto una scansione semestrale, il mio progetto didattico
era di produrre quattro manualetti, due di Meccanica e due di Scienza. Per gli
studenti di ingegneria, la Meccanica dei Solidi è principalmente meccanica delle
strutture descrivibili con un numero finito di parametri: al manuale di Statica,
disciplina formulata nel linguaggio del calcolo vettoriale e regolata da equazioni
algebriche, avrebbe fatto seguito quello di Dinamica, dove si devono formulare e
risolvere equazioni differenziali ordinarie. Quanto alla Scienza delle Costruzioni, il
suo primo oggetto è la meccanica delle strutture uni- o bidimensionali descritte da
campi, il comportamento delle quali è regolato da equazioni differenziali ordinarie
o alle derivate parziali; al manuale dedicato allo studio delle deformazioni di travi
e travature elastiche sarebbe seguito quello dedicato allo studio dello stato di
sforzo nelle travi.
In ognuno degli anni accademici successivi al 2002-2003, quelle tracce di lezione sono state completate e corrette, da me e da chi con me collaborava per
le esercitazioni o insegnava uno dei quattro corsi semestrali del pacchetto. In
qualche caso mi consta, in altri ho motivo di ritenere, che di quelle tracce ci si
sia talvolta disinvoltamente avvalsi anche in altri atenei: ciò che è reperibile in
rete è dai più ritenuto res nullius, ma quel che conta per gli adepti, naturalmente,
è che il verbo si diffonda senza troppo corrompersi. Anche per arginare abusi e
corruzioni, nel 2008 sono apparsi per i tipi di Aracne il terzo e il quarto dei manualetti dei quali ho detto, i cui contenuti sono stati poi riuniti–corretti, riveduti
e ampliati–nel volume intitolato “Lezioni di Scienza delle Costruzioni”, che è dal
2009 in catalogo presso lo stesso editore.
Nel licenziare per la stampa queste “Lezioni di Statica”, penso senza soverchio
dispiacere che il mio originale progetto didattico non sarà completato: perchè
una disciplina viva è necessario che la sua narrazione sia rinnovata alla luce dei
progressi nelle discipline fondanti o confinanti, e certo c’era gran bisogno di aggiornare l’ormai ultradatato impianto narrativo franco-tedesco della Scienza delle
Costruzioni all’italiana a seguito dei notevoli sviluppi che la Meccanica Razionale
dei Continui aveva avuto nella seconda metà del secolo scorso; ma conviene che
il narratore sia impegnato sul campo mentre attende alla narrazione, cosa che a
me per la dinamica delle strutture a numero finito di parametri non capiterà più.
Penso anche con gratitudine a coloro che mi hanno aiutato a dare alle tracce che
avevo redatto una forma conveniente per la pubblicazione: prima Paola Isabella
Valenzi, Andrea Micheletti, Vincenzo Nicotra e Giuseppe Tomassetti, poi ancora
Vincenzo Nicotra e Antonino Favata, con i quali sono anche in gran debito per
l’esecuzione di figure che hanno conferito piena leggibilità ai miei schizzi.
Paolo Podio-Guidugli
Roma, 17 agosto 2014
Indice
1 Richiami di Algebra Vettoriale
1.1 Spazio ambiente . . . . . . . . . . . . . . . . . . . .
1.2 Spazi vettoriali di dimensione finita . . . . . . . . .
1.2.1 Somma . . . . . . . . . . . . . . . . . . . . .
1.2.2 Prodotto . . . . . . . . . . . . . . . . . . . .
1.3 Operazioni tra vettori . . . . . . . . . . . . . . . . .
1.3.1 Prodotto scalare . . . . . . . . . . . . . . .
1.3.2 Rappresentazione in una base ortonormale .
1.3.3 Prodotto vettoriale . . . . . . . . . . . . . .
1.3.4 Prodotto vettoriale in una base ortonormale
1.3.5 Prodotto misto . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
7
9
9
10
10
10
14
15
24
26
2 Sistemi di Forze e Coppie
2.1 Nozione di forza . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Momento di una forza rispetto ad un polo . . . . . . . .
2.2 Sistemi di forze . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Asse centrale . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Nozione di coppia . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Sistemi di forze e coppie . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Riduzione di una forza ad un punto assegnato . . . . . .
2.4.2 Decomposizione di una forza secondo direzioni assegnate
2.5 Sistemi piani di forze e coppie . . . . . . . . . . . . . . . . . . .
2.5.1 Asse centrale . . . . . . . . . . . . . . . . . . . . . . . .
2.5.2 Sistemi nulli . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.3 Problemi di decomposizione . . . . . . . . . . . . . . . .
2.5.4 Poligono funicolare. Costruzione grafica dell’asse centrale
.
.
.
.
.
.
.
.
.
.
.
.
.
29
29
31
32
33
40
43
43
45
51
52
52
53
56
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
INDICE
3 Statica del Corpo Rigido
3.1 Tre esempi introduttivi . . . . . . . . . . . . . . . . . .
3.2 Cinematica . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Potenza di un sistema di forze e coppie . . . . . . . . .
3.4 Sistemi bilanciati di forze e coppie. Equazioni cardinali
3.5 Vincoli esterni . . . . . . . . . . . . . . . . . . . . . . .
3.5.1 Vincoli spaziali . . . . . . . . . . . . . . . . . .
3.5.2 Vincoli piani . . . . . . . . . . . . . . . . . . . .
3.6 Metodo delle forze e metodo delle potenze . . . . . . .
3.6.1 Ricerca di configurazioni di equilibrio . . . . . .
3.6.2 Ricerca di reazioni vincolari . . . . . . . . . . .
3.7 Metodo del potenziale . . . . . . . . . . . . . . . . . .
3.7.1 Derivata direzionale. Gradiente . . . . . . . . .
3.7.2 Potenziale di un campo di forza . . . . . . . . .
3.7.3 Equilibrio stabile, instabile, indifferente . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
61
61
65
68
70
72
73
76
78
78
80
84
86
86
87
4 Catene Piane di Corpi Rigidi
4.1 Metodo delle potenze . . . . . . . . . . . . . . . . . . . . .
4.1.1 Equilibrio di una catena di due travi priva di vincoli
4.1.2 Equilibrio di una catena di due travi vincolata . . .
4.2 Metodo degli equilibri parziali . . . . . . . . . . . . . . . .
4.3 Rigidità di una catena chiusa di tre travi . . . . . . . . . .
4.4 Cinematica di catene aperte . . . . . . . . . . . . . . . . .
4.4.1 Centro di rotazione istantanea . . . . . . . . . . . .
4.4.2 Atto di moto . . . . . . . . . . . . . . . . . . . . .
. . . .
esterni
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
93
93
94
96
99
103
104
105
107
5 Travature Piane con Elementi Elastici: Equilibrio
5.1 Introduzione . . . . . . . . . . . . . . . . . . . . . .
5.2 Travature capaci di moti rigidi . . . . . . . . . . . .
5.3 Modelli lineari di molle elastiche . . . . . . . . . . .
5.3.1 Molle estensionali . . . . . . . . . . . . . . .
5.3.2 Molle rotazionali . . . . . . . . . . . . . . .
5.4 Equilibrio di travature deformabili . . . . . . . . . .
5.4.1 Esistenza di soluzioni. Unicità . . . . . . . .
5.4.2 Principio di bilancio delle potenze . . . . . .
5.4.3 Principio di minimo dell’energia totale . . .
5.4.4 Lavoro dei carichi ed energia elastica . . . .
5.4.5 Sovrapposizione degli effetti. Reciprocità . .
5.5 Altri problemi di equilibrio . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
113
113
114
116
116
119
121
121
122
125
126
127
129
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
INDICE
5
6 Travature Piane con Elementi Elastici: Instabilità
6.1 Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 Instabilità per diramazione: analisi statica . . . . . . . . . .
6.3 Instabilità per diramazione: analisi dinamica . . . . . . . . .
6.4 Instabilità in presenza di imperfezioni . . . . . . . . . . . . .
6.4.1 Imperfezioni di carico . . . . . . . . . . . . . . . . . .
6.4.2 Imperfezioni di geometria . . . . . . . . . . . . . . .
6.5 Instabilità di travature a più parametri . . . . . . . . . . . .
6.5.1 Più parametri cinematici . . . . . . . . . . . . . . . .
6.5.2 Più parametri di carico . . . . . . . . . . . . . . . . .
6.6 L’instabilità per diramazione come problema agli autovalori .
6.7 Verso un modello continuo di instabilità per diramazione . .
6.8 Instabilità per scatto . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
137
137
138
144
146
147
148
149
149
152
153
155
157
A Appendice. Geometria dei sistemi piani di masse
A.1 Prodotto diadico di vettori, tensori . . . . . . . . .
A.2 Trasformazioni di coordinate cartesiane ortogonali .
A.3 Centro di massa. Momenti del primo ordine . . . .
A.4 Momenti del secondo ordine . . . . . . . . . . . . .
A.5 Il tensore d’inerzia . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
161
161
163
166
172
174
Indice analitico
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
179
Capitolo 1
Richiami di Algebra
Vettoriale
1
Molti tra gli oggetti della Meccanica – ad esempio, forze e velocità – sono rappresentati e manipolati come campi vettoriali su corpi, cioè, come applicazioni a
valori vettoriali definite su regioni di uno spazio ambiente, alle quali si attribuisce
sostanza materiale. Conviene quindi cominciare il nostro studio della Meccanica descrivendone senza eccessive formalità lo spazio ambiente, per poi passare
brevemente in rivista le principali strutture algebriche degli spazi vettoriali di
dimensione finita.
1.1
Spazio ambiente
Lo spazio in cui operiamo è lo spazio euclideo E a 3 dimensioni, i cui elementi
sono i punti P , Q, . . . . La differenza tra due punti è un vettore, un elemento
dello spazio delle traslazioni VE associato con E:
P − Q = v ∈ VE .
VE è uno spazio vettoriale tridimensionale.1 Per giustificare la nomenclatura,
basta pensare di disporre di una copia E � di E e pensare P, Q come punti di
entrambi questi spazi: v individua una particolare isometria (≡ applicazione
biunivoca che lascia inalterate le distanze tra punti) tra E e E � , la traslazione che
1
Per dimensione di uno spazio euclideo si intende la dimensione del suo spazio delle traslazioni. Spiegheremo come si assegna ad uno spazio vettoriale la sua dimensione alla fine della
prossima sezione.
8
porta Q ∈ E su P ∈ E � :
Richiami di Algebra Vettoriale
Q + v = P. 2
Osservazione. Le ultime due relazioni sussumono che siano ben definite e mutuamente consistenti, dato uno spazio euclideo, le operazioni di differenza tra
punti, che produce un vettore dello spazio delle traslazioni associato, e di somma
tra un punto e un vettore dello spazio delle traslazioni, che produce un punto. Si
noti che l’operazione di somma tra punti è priva di senso.
Scelto in E un punto O, il vettore posizione di P rispetto all’origine O si indica
nei modi alternativi
−→
P − O = OP .
Presi tre elementi e1 , e2 , e3 di VE , mutuamente ortogonali e di modulo unitario,
consideriamo in E tre rette orientate per l’origine, ordinatamente parallele e equiverse a questi vettori. Ottenuti per proiezione ortogonale di P i punti P1 , P2 e
P3 (Fig. 1.1),
Figura 1.1
abbiamo che
−−→
OP1 = p1 e1 ,
p1 ∈ R,
etc.
e quindi che
3
−→ −−→
OP =
OPi .
i=1
I numeri reali pi (i=1,2,3) sono tanto le coordinate del punto P quanto le compo−→
nenti del vettore posizione OP nel riferimento cartesiano ortonormale {O; e1, e2 , e3 }.
2
Anche le rotazioni sono isometrie, e con le traslazioni ne esauriscono la classe; incontreremo
le rotazioni più avanti. Per visualizzare un’isometria, si possono pensare E e E come due fogli
di carta sovrapposti e immaginare di far traslare o ruotare il primo foglio rispetto al secondo.
1.2 Spazi vettoriali di dimensione finita
9
Osservazione. Fissato il riferimento, ciascuna delle corrispondenze
E � P ↔ (p1 , p2 , p3 ) ∈ R3
−→
e E � P ↔ OP ∈ VE
è biunivoca. È bene tuttavia non confondere un punto dello spazio euclideo con
la tripletta delle sue coordinate o con il suo vettore posizione: in primo luogo,
punti, triplette e vettori sono oggetti matematici di natura diversa; in secondo
luogo, variando il riferimento, si può far corrispondere ad uno stesso punto quante
triplette e quanti vettori posizione si voglia.
1.2
Spazi vettoriali di dimensione finita
Indichiamo con V un generico spazio vettoriale sul campo R dei numeri reali,
di dimensione finita. Le operazioni fondamentali tra elementi di V e di R sono la
somma tra vettori e il indexprodotto!di un numero reale per un vettoreprodotto
di un numero reale per un vettore.
1.2.1
Somma
Ad ogni coppia di vettori a, b ∈ V , questa operazione associa il vettore
(a + b) ∈ V :
“somma” : V × V → V, (a, b) →
� a +b.
La somma è definita per astrazione a partire dalla classica “regola del parallelogramma”:
Figura 1.2
Le proprietà fondamentali sono: per ogni scelta di a, b, c ∈ V ,
(i) a + b = b + a (commutatività);
(ii) a + 0 = a (esistenza dell’elemento neutro, indicato con 0);
(iii) (a + b) + c = a + (b + c) (associatività).
10
Richiami di Algebra Vettoriale
1.2.2
Prodotto
Ad ogni coppia costituita da uno scalare α ∈ R e un vettore a ∈ V , questa
operazione associa il vettore (αa) ∈ V :
“prodotto” : R × V → V,
(α, a) �→ αa .
Le proprietà fondamentali sono: per ogni scelta di α, β ∈ R e di a, b ∈ V ,
(i) α(βa) = (αβ)a (associatività);
(ii) α(a + b) = αa + αb (distributività rispetto alla somma di vettori );
(iii) (α + β)a = αa + βa (distributività rispetto alla somma di scalari).
Dato un insieme di vettori non nulli vi ∈ V (i = 1, . . . , N), li si dice linearmente dipendenti se è nulla almeno una loro combinazione lineare non banale
(cioè, a coefficienti non tutti nulli):
N
αi vi = 0;
i=1
altrimenti, li si dice linearmente indipendenti. La dimensione dello spazio vettoriale V è pari al numero massimo di suoi elementi linearmente indipendenti.
1.3
1.3.1
Operazioni tra vettori
Prodotto scalare
Questa operazione associa a due elementi a, b ∈ V lo scalare (a · b) ∈ R:
“prodotto scalare” : V × V → R,
(a, b) �→ a · b .
Il prodotto scalare possiede le seguenti proprietà: per ogni scelta di a, b, c ∈ V
e di α ∈ R,
(i) a · b = b · a (commutatività);
(ii) a · (b + c) = a · b + a · c (distributività rispetto alla somma di vettori );
(iii) α(a · b) = (αa) · b (associatività rispetto al prodotto per scalari );
(iv) a · a ≥ 0,
a · a = 0 ⇔ a = 0 (positività).
1.3 Operazioni tra vettori
11
Varie nozioni di algebra vettoriale si introducono in termini di prodotto scalare,
in primis la nozione di ortogonalità:
a, b ∈ V si dicono ortogonali ⇔ a · b = 0.
Inoltre, il modulo di un vettore si definisce come
|a| := (a · a)1/2 ,
il versore di un vettore a �= 0 come
vers a = |a|−1 a ;
dunque,
v = |v | vers v .
Infine, per angolo tra due vettori a, b ∈ V si intende il numero reale
quindi,
:= arccos a · b ;
ab
|a||b|
= vers a · vers b .
cos ab
Osservazione. Se a e b sono vettori ortogonali, scriveremo talvolta a⊥b .
Inoltre, quando ci parrà opportuno alleggerire la notazione, indicheremo il modulo
di un vettore con la lettera romana corsiva corrispondente: ad esempio, a = |a|,
b = |b|, etc..
Esercizi
Per familiarizzarci con la nozione di prodotto scalare, ne mostriamo l’uso per
provare con il formalismo dell’algebra vettoriale alcune semplici proposizioni di
geometria piana.
1. Dimostrare il Teorema di Pitagora.
Figura 1.3
Soluzione. Nel triangolo rettangolo in figura, i vettori a e b corrispondono ai
cateti; il vettore che corrisponde all’ipotenusa è c = a − b. Ne segue che
c · c = c2 = (a − b) · (a − b) = a2 − 2 a · b + b2
⇒
c2 = a2 + b2 .
12
Richiami di Algebra Vettoriale
2. Dimostrare che, in un triangolo rettangolo, l’altezza relativa all’ipotenusa è
media proporzionale tra le proiezioni dei cateti sull’ipotenusa stessa.
Figura 1.4
−−→ −−→
Soluzione. Dalla figura: AH + HC = c. Ne segue che
−−→
−−→ −−→
−−→
|AH|2 + |HC|2 + 2AH · HC = |c|2 ,
donde, con l’uso reiterato del teorema di Pitagora, si ottiene:
−−→ −−→
a2 − BH 2 + b2 − BH 2 + 2AH · HC = c2
⇒
−−→
−−→ −−→
|BH|2 = AH · HC .
3. Mostrare che i tre vettori:
a = 3e1 − 2e2 + e3 ,
b = e1 − 3e2 + 5e3 ,
c = 2e1 + e2 − 4e3 ,
possono corrispondere ai lati di un triangolo rettangolo.
Soluzione. La verifica è immediata, osservando che uno dei due vettori è somma
degli altri due (a = b + c) e che due dei vettori sono perpendicolari fra loro
(a · c = 0).
4. Dimostrare il Teorema del Coseno (di Carnot):
b2 = a2 + c2 − 2ac cos β .
Figura 1.5