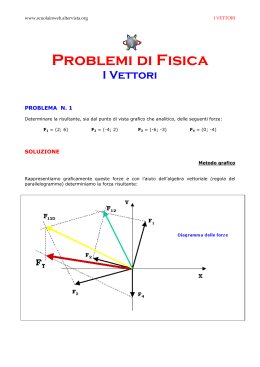
Prodotto vettoriale
Dati due vettori 𝒂 e 𝒃 , il prodotto vettoriale 𝒄 = 𝒂 × 𝒃 è un vettore che
gode delle proprietà seguenti:
• il modulo di 𝒄 è dato da absinθ, dove θ è l’angolo minore di 180°
compreso tra 𝒂 e 𝒃
• la direzione di 𝒄 è perpendicolare al piano individuato da 𝒂 e 𝒃
• il verso di 𝒄 è calcolato mediante diverse regole
c
b
θ
a
Regola della vite destrorsa o del cavatappi:
Si orienta la vite
perpendicolarmente al piano
individuato dai due vettori.
Si ruota la vite nel verso che
corrisponde alla rotazione
del primo vettore verso il
secondo. Il verso di
avanzamento della vite indica
il verso del prodotto vettoriale
c
b

a
La regola della mano destra
• Prima formulazione
– Si dispone il pollice lungo il primo
vettore
– Si dispone l’indice lungo il secondo
vettore
– Il verso del medio individua il verso
del prodotto vettoriale
• Seconda formulazione (detta da alcuni
Regola di Fonzie)
– Si chiude a pugno la mano destra
mantenendo sollevato il pollice
– Le dita chiuse a pugno devono
indicare il verso in cui il primo vettore
deve ruotare per sovrapporsi al
secondo in modo che l’angolo θ di
rotazione sia minore di 180°
– Il verso del pollice individua il verso
del prodotto vettoriale
b
a×b
a
a×b
b
a
• ha come verso quello secondo il quale si deve
disporre un osservatore con i piedi nel punto O
d’applicazione dei due vettori affinché possa veder
ruotare il vettore u in senso antiorario dell’angolo 
perché si sovrapponga al vettore v .
c
b

O
a
Proprietà del prodotto vettoriale
• Il modulo del prodotto vettoriale è pari all’area del parallelogramma
individuato dai due vettori
b
θ
a
Area (𝒂; 𝒃) = a.b.sen
Precisamente, si può considerare il parallelogramma avente per lati i
due vettori in esame. Indicando  l’angolo convesso formato dai due
vettori u,v si riconosce che l’altezza del parallelogramma relativa al lato
determinato dal vettore u è data dal prodotto v*sin (confrontare la
figura) per cui l’area del parallelogramma è:
Il prodotto vettoriale è nullo se i due vettori sono paralleli (θ=0)
Il prodotto vettoriale gode della proprietà anticommutativa:
 
 
b  a  a  b
Prodotto vettoriale in componenti cartesiane
Tenendo conto che i versori degli assi cartesiani sono a due a
due perpendicolari fra loro, ed applicando la regola della mano
destra, si hanno le seguenti relazioni:
iˆ  iˆ  0
ˆj  iˆ   kˆ
kˆ  iˆ  ˆj
iˆ  ˆj  kˆ iˆ  kˆ   ˆj
ˆj  ˆj  0
ˆj  kˆ  iˆ
kˆ  ˆj  iˆ kˆ  kˆ  0
Pertanto, esprimendo i vettori in termini delle loro componenti
cartesiane, si ha che:
  ˆ
a  b  i (a y bz  a z b y )  ˆj(a z bx  a x bz )  kˆ(a x b y  a y bx )
iˆ
 
a  b  ax
bx
ˆj
ay
by
kˆ
az
bz
HALLIDAY - capitolo 3 problema 19
Due vettori 𝒓 ed 𝒔 giacciono nel piano xy. I loro moduli sono
rispettivamente di 4,50 e 7,30 unità, e le loro direzioni sono
rispettivamente di 320° e 85° misurate in senso antiorario dal semiasse
positivo delle x. Quali sono i valori di 𝒓 ∙ 𝒔 e 𝒓 × 𝒔?
s x  7,30  cos(85 )  0,636
y
s y  7,30  sin(85 )  7,27
s
85°
320°
x
O
rx  4,50  cos(320  )  3,45
r
ry  4,50  sin(320 )  2,89
Prodotto scalare:
 
r  s  (3,45iˆ  2,89ˆj)  (0,636iˆ  7,27ˆj) 
3,45  0,636  ( 2,89) 7,27  18,8
Alternativamente, possiamo calcolare l’angolo minore di 180° fra i due vettori e
sfruttare la definizione di prodotto scalare.
α  85  (360  320 )  125
y
s
 
r  s  4,50 7,30  cos(125 )  18,8
α
320°
85°
x
O
r
iˆ
 
r  s  3,45
0,636
Prodotto vettoriale:
ˆj
 2,89
7,27
kˆ
0 
0
kˆ3,45  7,27  ( 2,89)  0,636   26,9kˆ
Alternativamente, possiamo calcolare il modulo del prodotto vettoriale con la
definizione e stabilire il suo verso usando la regola della mano destra.
 
r  s  4,50 7,30  sin(125 )  26,9
y
320°
s
Applicando la regola della
mano destra si può verificare
che il prodotto vettoriale è
diretto in verso uscente
x del foglio, e
rispetto al piano
quindi concorde con il
semiasse z positivo
85°
O
r