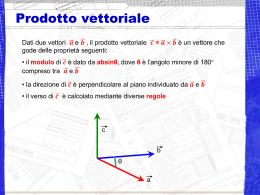
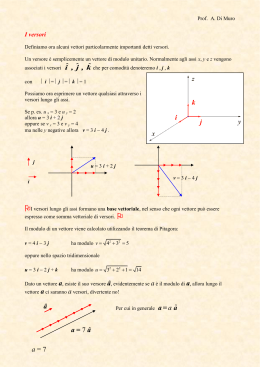
I vettori
Grandezze scalari:
vengono definite dal loro valore numerico
esempi: lunghezza di un segmento, area di una figura piana,
temperatura di un corpo, ecc.
Grandezze vettoriali
vengono definite, oltre che dal loro valore numerico, da una
direzione e da un verso
esempi: velocità di un corpo, forza agente su un corpo, ecc.
Vettori nel piano
y
B’

v
’
A

modulo di v = lunghezza
B
del segmento AB

vè
la direzione di
definita dall’angolo φ
φ
A’
componente vx =
lunghezza di A’B’
’
O
A

v  (v x’ , v y )

v  v x2  v 2y
  arctan
vy
vx
B
’
x
componente vy =
lunghezza di A’’B’’
Versori
versore = vettore di lunghezza unitaria
y
î (1,0) = versore dell’asse x
ĵ(0,1) = versore dell’asse y
ĵ
î
0
x
Prodotto di un vettore per uno scalare
Dati uno scalare c ed un vettore v, si definisce il
prodotto u=cv.
Il vettore u è parallelo a v. Il modulo di u è dato da:


u  c v
Il verso di u è lo stesso di v se c>0, è opposto a quello
di v se c<0
Somma di due vettori
y
Il vettore somma
c=a+b è la
diagonale del
parallelogramma
avente per lati i
vettori a e b
by
a
cy
ay
c
θ
b
ax
0
c x  a x  bx
c y  a y  by
bx
cx

c 
x
2
2
 
a  b  2 a b cosθ
Differenza di due vettori
La differenza a - b si calcola sommando al vettore a
il vettore -b, opposto del vettore b
y
c=a-b
a
-b
b
0
x
Somma di N vettori
Dati i vettori a1, a2, ... , aN il vettore somma b = a1+a2+ ... +aN si
calcola nel modo seguente:
•si costuisce la spezzata formata dai vettori a1, a2, ..., aN
•si congiungono i due estremi liberi di tale spezzata
y
a2
a1
a3
a4
b
0
x
bx  a1x  a 2x  ...  a Nx
b y  a1y  a 2y  ...  a Ny
Scomposizione di un vettore lungo due
direzioni orientate r ed s
s
vs
v
vr
r
Determinare due vettori vr e vs paralleli rispettivamente a r
ed s e tali che v = vr + vs
Dall’estremo libero di v si mandano la parallela a r verso s
e la parallela a s verso r. Restano così definiti i vettori vr e vs
Scomposizione lungo gli assi cartesiani
Si tratta di un caso particolare di scomposizione, lungo le
direzioni ortogonali degli assi cartesiani
y
vy ĵ
v
vx î

v  v x iˆ  v y ˆj
x
Vettori nello spazio
z

v  v x iˆ  v y ˆj  v z kˆ
^
vz k
v

2
2
2
v  v x  v y  vz
θ
vy ĵ
vx î
x
φ
y
La direzione di v risulta
definita dagli angoli θ e φ
vz
θ  arccos 
v
  arctan
vy
vx
Prodotto scalare
Dati due vettori a e b, il prodotto scalare tra a e b è una
grandezza scalare definita nel modo seguente:
 
a  b  a b cosα
b
Il prodotto scalare tra a e b è
un numero che è pari al
prodotto del modulo di a per
la componente di b lungo la
direzione di a
α
a
bcosα
Ovviamente il prodotto
scalare a · b è anche pari al
prodotto del modulo di b per
la componente di a lungo la
direzione di b
Prodotto scalare in componenti cartesiane
Tenendo conto del fatto che i versori degli assi cartesiani sono
a due a due perpendicolari fra loro, si ha che:
iˆ  iˆ  1 iˆ  ˆj  0 iˆ  kˆ  0
ˆj  iˆ  0 ˆj  ˆj  1 ˆj  kˆ  0
kˆ  iˆ  0 kˆ  ˆj  0 kˆ  kˆ  1
Di conseguenza, esprimendo i vettori in termini delle loro
componenti cartesiane, si ha:

a  a x iˆ  a y ˆj  a z kˆ

b  bx iˆ  b y ˆj  bz kˆ
Caso particolare: b = a
 
a  b  a x bx  a y b y  a z bz
 
2
2
2
2
a  a  a x  a y  az  a
Prodotto vettoriale
Dati due vettori a e b, il prodotto vettoriale c = a × b è un
vettore che gode delle proprietà seguenti:
• il modulo di c è dato da absinθ, dove θ è l’angolo minore di
180° compreso tra a e b
• la direzione di c è perpendicolare al piano individuato da a e b
• il verso di c è calcolato applicando la regola della mano destra
c
b
θ
a
La regola della mano destra
b
Prima formulazione
Si dispone il pollice lungo il primo vettore
Si dispone l’indice lungo il secondo
vettore
Il verso del medio individua il verso del
prodotto vettoriale
a×
b
a
Seconda formulazione
Si chiude a pugno la mano destra
mantenendo sollevato il pollice
Le dita chiuse a pugno devono indicare il
verso in cui il primo vettore deve ruotare
per sovrapporsi al secondo in modo che
l’angolo θ di rotazione sia minore di
180°
Il verso del pollice individua il verso del
prodotto vettoriale
a×
b
b
a
Proprietà del prodotto vettoriale
Il modulo del prodotto vettoriale è
pari all’area del parallelogramma
individuato dai due vettori
Il prodotto vettoriale è nullo se i
due vettori sono paralleli (θ=0)
Il prodotto vettoriale gode della
proprietà anticommutativa:
 
 
b  a  a  b
b
θ
a
Prodotto vettoriale in componenti cartesiane
Tenendo conto che i versori degli assi cartesiani sono a due a due
perpendicolari fra loro, ed applicando la regola della mano destra, si
hanno le seguenti relazioni:
iˆ  iˆ  0
ˆj  iˆ   kˆ
kˆ  iˆ  ˆj
iˆ  ˆj  kˆ iˆ  kˆ   ˆj
ˆj  ˆj  0
ˆj  kˆ  iˆ
kˆ  ˆj  iˆ kˆ  kˆ  0
Pertanto, esprimendo i vettori in termini delle loro componenti
cartesiane, si ha che:
  ˆ
a  b  i (a y bz  a z b y )  ˆj(a z bx  a x bz )  kˆ(a x b y  a y bx )
iˆ
 
a  b  ax
bx
ˆj
ay
by
kˆ
az
bz
Posizione di un punto nello spazio
Una volta fissato un sistema di riferimento nello spazio, la posizione
di un qualsiasi punto P dello spazio è individuata tramite il vettore
posizione, ossia il vettore r che congiunge l’origine con il punto P
y
P
yĵ
r
O
xî
x
In coordinate cartesiane, se P(x,y) il vettore posizione è dato da:

r  xiˆ  yˆj
Posizione in coordinate polari
La posizione di P è sempre data dal vettore posizione r
Il vettore posizione r è ora espresso in termini dei versori ûr e ûφ
ûφ
P
r
ûr

r  ruˆ r
φ
O
asse polare
ûr = versore nella direzione radiale
ûφ = versore perpendicolare a ûr nella direzione delle φ crescenti
I versori ûr e ûφ dipendono dalla posizione del punto P !!!