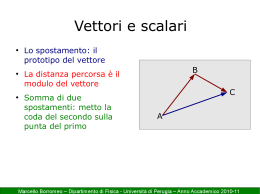
Grandezze scalari e vettoriali
Esistono due tipi di grandezze fisiche.
a) Grandezze scalari specificate da un valore numerico (positivo
negativo o nullo) e (nel caso di grandezze dimensionate) da una appropriata
unita’ di misura
Esempi: tempo, massa , temperatura, energia…
Queste grandezze sono normalmente indicate da un carattere tipografico
normale.
b) Grandezze vettoriali specificate da un valore numerico positivo
(modulo) con una appropriata unita’ di misura, da una direzione e da
un verso
Esempi: spostamento, velocita’, accelerazione, forza…
Queste grandezze sono normalmente indicate da un carattere in grassetto, o
da un carattere sormontato da una freccia, o da un carattere sottolineato
(notazione preferita dai matematici).
Inoltre graficamente i vettori si indicano con una freccia la cui lunghezza e’
proporzionale al modulo del vettore.
• Esempio vettore spostamento:
→
S SS
Se un corpo si sposta da un punto A ad un punto B distanti
fra loro 1 m, per definire in modo completo tale
spostamento sara’ necessario un vettore caratterizzato da:
modulo: uguale 1 m;
direzione: retta che congiunge A e B;
verso : da A a B.
• Il simbolo di un vettore compreso fra due
sbarrette verticali indica il modulo del
vettore stesso.
Ad Esempio S  indica il modulo del
vettore S
• Due vettori sono uguali se hanno
modulo direzione e verso uguali
La sua direzione e' la linea retta nello
spazio su cui giace il vettore, il suo
modulo e' la lunghezza del vettore, il suo
verso e' l'orientazione del vettore sulla
sua retta.
Modulo, direzione e verso
saranno definiti di volta in
volta secondo la grandezza
vettoriale in esame
Somma fra vettori
Dati due vettori A e B qualsiasi, come possiamo calcolare graficamente la loro
somma R=A+B , detta anche vettore risultante?
Si puo’ procedere in due modi:
a)Spostare il vettore B, mantenendolo sempre parallelo a se stesso, finche la sua coda coincida con la punta
di A. Il vettore R=A+B avra’ la coda che coincide con la coda di A e la punta che coincide con la punta di B.
b)Spostare il vettore B, mantenendolo sempre parallelo a se stesso, finche’ la sua coda coincide con la coda
di A. Disegnare il parallelogramma avente per lati i due vettori cosi’ ottenuti. Il vettore R=A+B e’
rappresentato dalla diagonale del parallelogramma ed ha la coda coincidente con quella di A e B
Notiamo che il vettore R giace sul piano identificato da A e B
La somma vettoriale cosi’ definita gode delle seguenti proprieta’:
a)proprieta’ commutativa esempio : A+B=B+A
b)proprieta’ associativa esempio: (A+B)+C= A+(B+C)
Differenza fra vettori
Dato un vettore A il suo vettore opposto –A e’ definito come quel vettore avente
lo stesso modulo e direzione di A ma verso opposto.
In base alle regole definite precedentemente si avra’
A+(-A)=0
La differenza fra due vettori A e B e’ definita come la somma fra i vettori A e -B
C=A-B=A+(-B)
Prodotto fra uno scalare ed un vettore
Il prodotto di un vettore A per uno scalare k da’ come risultato
un vettore M = kA
Se k>0 M ha la stessa direzione e verso di A e modulo
M = k A
Se k<0 M ha la stessa direzione di A, verso opposto ad A e modulo
M = k A
Esempio
Se k=-1 si ha
M=-A
Cioe’ il vettore M ha stessa direzione e modulo di A ma verso opposto.
In altre parole il vettore M e’ il vettore opposto di A.
Versori e componenti
Si definiscono versori dei vettori di lunghezza unitaria (modulo=1) e privi di
dimensioni (cioe’ senza unita’ di misura associata). I versori sono solitamente
utilizzati per indicare una direzione ed un verso.
I versori vengono a volte indicati con la stessa lettera dell’eventuale vettore da
cui derivano sormontata dal simbolo ^. Ad ogni vettore generico A e’ possibile
associare il suo versore  avente modulo unitario e stessa direzione e verso di A
Quindi qualsiasi vettore puo’ essere espresso come il prodotto del suo modulo
per il suo versore. Esempio:
A= A Â
Come sara’ chiaro fra poco particolare importanza hanno i versori aventi direzione
e verso dei tre assi ortogonali x, y, z, di un sistema cartesiano. Tali versori sono
solitamente indicati con x , y, z oppure i, j, k oppure i, j, k (carattere grassetto).
Dato un generico vettore A ed asse orientato r, siano P1 e P2 le proiezioni
ortogonali della coda e della punta di A sull’asse r.
A
Si definisce componente scalare Ar del vettore A rispetto all’asse r
quel numero relativo il cui valore assoluto e’ la lunghezza del
segmento P1 P2 ed il cui segno e’ positivo o negativo secondo che il
segmento orientato P1 P2 abbia verso uguale o opposto a quello dell’asse r.
Ar= A cos α
Componenti cartesiane
Dato un vettore arbitrario a ed un sistema di assi cartesiani Oxyz le componenti
ax, ay, az, del vettore a rispetto agli assi x, y, z prendono il nome di componenti
cartesiane. Da quanto detto ax, ay, az, possono essere positive negative o nulle.
a
Quindi detti α, β, e γ gli angoli che il vettore a forma con gli assi x, y, z,
(dove 0o ≤α, β,γ≤ 180o ) avremo:
ax = a cos α
ay= a cos β
az= a cos γ
Inoltre applicando due volte il teorema di Pitagora (vedi figura) il
modulo di un vettore puo’ essere espresso tramite le sue componenti
a = [( ax)2+( ay )2+( az )2 ]1/2
Da tutto quanto detto sinora segue che dato un generico vettore A esso puo’
sempre essere espresso tramite le sue componenti cartesiane nel seguente modo:
A=ax i + ay j + azk
Ad esempio per un vettore che giace sul piano
x, y avremo az= 0 quindi:
A= Ax i + Ay j
Somma fra vettori, metodo analitico
Tramite l’utilizzo delle componenti cartesiane possiamo sommare
analiticamente due o piu’ vettori.
Siano A e B due vettori generici espressi tramite le loro componenti cartesiane
A= axi + ay j + azk ; B=bxi + by j + bzk
e si voglia calcolare il vettore risultante
R=A+B
Per la proprieta’ associativa le componenti di ciascun vettore possono essere
raggruppate secondo la direzione. Pertanto si avra’:
R =(axi + ay j + azk +bxi + by j + bzk)=
= (ax+bx)i + (ay+by)j + (az+ bz)k
In altre parole:
Rx =(ax + bx); Ry = (ay + by); Rz = (az + bz)
Tale procedura, utilizzabile in generale per la somma di un qualsiasi numero
di vettori, puo’ essere ‘visualizzata’ semplicemente per la somma di due
vettori giacenti sul piano xy.
Prodotto scalare
Esistono due modi per moltiplicare fra loro due vettori.
1)Prodotto Scalare che ha come risultato uno scalare
2)Prodotto vettoriale che ha come risultato un vettore.
Dati due vettori a e b il loro prodotto scalare si indica come a • b ed e’
cosi’ definito:
a • b = a   b  cos Φ
Dove Φ e’ l’angolo compreso fra i due vettori a e b .
Dalla definizione di prodotto scalare capiamo che:
1)Il segno del prodotto scalare dipende unicamente dal valore dell’angolo Φ
2)Il prodotto scalare e’ sempre nullo se Φ=90o
3)Il prodotto scalare puo’ essere pensato come il prodotto del modulo di a per
la componente (scalare) di b rispetto ad a, o come prodotto del modulo di b
per la componente (scalare) di a rispetto b.
4) Per il prodotto scalare vale la proprieta’ commutativa e la proprietà
distributiva rispetto alla somma.
5)Il prodotto scalare di un vettore qualsiasi per se stesso da come risultato il
modulo quadro del vettore cioe’:
a • a = a  a  cos 0 =  a 2
Calcolo del prodotto scalare tramite le componenti
Dato un sistema di assi cartesiani Oxyz, a cui associamo i versori i, j, k, dalla
definizione di prodotto scalare segue che
il prodotto scalare fra due versori sara uguale a :
1 nel caso di prodotto scalare di un versore per se stesso (i•i = j•j = k•k = 1);
0 nel caso di prodotto scalare di un versore per uno differente (i•k = i•j = j•k = 0);
(i versori sono ortogonali)
Pertanto dati due vettori espressi tramite le loro coordinate cartesiane si avra’:
a • b = (axi + ay j + azk ) • (bxi + by j + bzk)=
= axbx + ayby + azbz
Cioe’ il prodotto scalare fra due vettori e’ uguale alla somma
dei prodotti delle componenti cartesiane corrispondenti.
Esempio:
Dati i vettori: A= 6.0 i –8.0 j e B= -4.0 i + 6.0 k calcolare :
1)Il vettore R=A-B; 2)I moduli di A e B
3)Il coseno dell’angolo compreso fra A e B
4)Il versore di A espresso tramite le sue componenti cartesiane
1) R=(6.0-(-4.0)) i –8.0 j –6.0 k = 10 i –8.0 j –6.0 k
2) A= [6.02 + (-8.0)2]1/2 = 10;
B= [(-4.0)2 + (+6.0)2]1/2 = 7.2
3) Sappiamo che A • B =  A  B  cos Φ
Ma A • B = 6.0x(-4.0) + (-8.0)x0 + 0x6.0 = -24 quindi
cos Φ = (A • B ) /( A  B ) = - 0.33
4) Â = A /A= 0.60 i – 0.80 j
Prodotto vettoriale
Dati due vettori a e b il loro prodotto vettoriale si indica come a x b
ed e’ un vettore c
c= a x b
che ha:
1) modulo pari a  c =  a   b  sen Φ, dove
Φ e’ l’angolo piu’ piccolo formato dai due vettori;
2) direzione perpendicolare al piano individuato
dai vettori a e b ;
3) verso che puo’ essere individuato ad esempio
tramite la ‘regola della mano destra’. Disegnati
a e b a partire dallo stesso punto di applicazione
si immagini di afferrare con le dita della mano
destra la perpendicolare ad a e b in modo da
spingere a verso b passando attraverso l’angolo
piu’ piccolo. Il pollice indichera’ il verso di c.
Dalla definizione di prodotto vettoriale capiamo che
1)Il prodotto vettoriale e’ sempre nullo se Φ=0o o 180o
2) Per il prodotto vettoriale non vale la proprieta’ commutativa infatti:
a x b = -b x a
3)Il prodotto vettoriale di un vettore qualsiasi per se stesso o, in generale, di
due vettori paralleli e’ nullo.
Dato un sistema di assi cartesiani
i prodotti vettoriali fra i versori degli assi
sono:
ixi=0;jxj=0;kxk=0
ixj=-jxi=k
kxi=-ixk=j
jxk=-kxj=i
Calcolo del prodotto vettoriale
tramite le componenti
Dati due vettori a e b espressi tramite le loro componenti cartesiane si ha:
a x b = (axi + ay j + azk) x (bxi + by j + bzk) =
= ax bx (ixi) + axby(ixj) + axbz(ixk) +
+aybx(jxi)+ayby(jxj) + aybz(jxk)+
+azbx(kxi) + azby(kxj)+azbz(kxk)=
tenendo presente i risultati dei prodotti vettoriali fra i versori
i, j, k dopo alcuni passaggi si ha
= (aybz-azby)i + (azbx-axbz)j +(axby-aybx)k
Questo risultato puo’ essere scritto in una forma mnemonica piu’ conveniente
sotto forma di determinante:
si sviluppa secondo gli
elementi della prima riga
i j k
a x b = ax ay az
bx by bz
Esempio :
Dati i vettori: A= 6.0 i –8.0 j e B= -4.0 i + 6.0 k calcolare il seno dell’angolo
compreso usando la definizione di prodotto vettoriale.
Sappiamo che  A x B  =  A  B  sen Φ
i j k
A x B = +6 -8 0
-4 0 +6
= (-48-0)i +(-36+0)j +(0-32)k
A x B  = [(-48)2 + (-36)2 + (-32)2 ]1/2 = 68
sen Φ = A x B /( A  B ) = 0.94
Alcuni quesiti di verifica:
1) Quale e’ la differenza fra grandezze fisiche scalari e vettoriali?
2) Da cosa e’ caratterizzato un vettore?
3) Il modulo di un vettore puo’ essere negativo?
4) Cosa e’ un versore?
5) Cosa si intende per componenti cartesiane di un vettore?
6) Dato un vettore espresso tramite le sue componenti cartesiane siete in grado
di calcolare: il corrispondente versore, il suo modulo, gli angoli che il
vettore forma con gli assi x,y,z ?
7)Dati due vettori espressi tramite le loro componenti cartesiane siete in grado
di calcolare: la loro somma, il loro prodotto scalare, il loro prodotto
vettoriale, l’angolo fra loro compreso?
8)Quale deve essere l’angolo formato da due vettori affinche’ il loro prodotto
scalare (vettoriale) sia nullo?