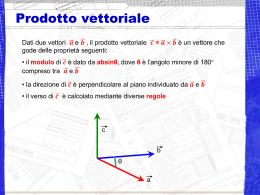
Le grandezze vettoriali e la loro
somma
Come fare lezione di matematica e
fisica anche attraverso modelli costruiti
dalla classe
Il parallelogramma articolato
•  Per la costruzione del
modello è necessario
prendere quattro
asticelle di materiale
rigido, come legno o
cartoncino da scatola,
uguali a due a due e
unirle con ferma
campioni per formare un
parallelogramma in
modo che la figura sia
mobile.
Il rombo articolato
•  Questo modello serve
per capire la somma di
vettori che hanno la
stessa lunghezza, ma
direzione variabile.
•  Vedremo ora in che
modo.
Cosa sono i vettori
Bisogna prima ricordare le
tre principali caratteristiche
dei vettori, che abbiamo
appreso con lo studio delle
traslazioni.
1)  La direzione, che è
l’elemento comune a tutte
le rette parallele;
2)  Il verso, che viene indicato
con una freccia
3)  Il modulo, che è la misura
del vettore stesso.
Sono equipollenti vettori che
hanno la stessa direzione,
lunghezza e verso.
Vettori e spostamento
• 
1. 
2. 
3. 
È lo spostamento nello spazio di un oggetto,
ma anche di un “punto geometrico” che
suggerisce le caratteristiche di un vettore
Quanto è lungo lo spostamento? È la
lunghezza del segmento AB ed è
sorprendente perché lo spostamento da A a
B è sempre il segmento AB, anche se il
percorso è frastagliato, curvo, molto più
lungo.
La direzione è la retta su cui giace il
segmento
Il verso è quello che va da A (coda) a B
(testa).
B
A
Somma di spostamenti e di
vettori
•  Come si sommano i vettori?
Ce lo suggerisce sempre la somma
di due spostamenti: se prima mi
sposto secondo il vettore b e poi
secondo il vettore a, lo
spostamento totale, a + b, è il lato
che chiude il triangolo, nel verso
indicato nella figura. Tale lato è
anche diagonale del
parallelogramma, costruito su a e
b.
La somma cambia
•  La somma dei due vettori cambia,
anche se il loro modulo resta invariato.
Si vede bene articolando il
parallelogramma:la diagonale cambia.
Senza il modello è facile essere
indotti in errore.
•  Nella figura è evidenziato l’angolo
formato dai due vettori (quello formato
dai loro versi positivi).
Facendo cambiare l’angolo, cambia di
conseguenza anche la diagonale, cioè
la diagonale è funzione dell’angolo e
l’angolo è la variabile indipendente.
Il modello
Un caso limite: α = 0°
• 
Spostando il parallelogramma si
vede che al diminuire dell’angolo α
tra i due vettori, la diagonale
cresce sempre di più, fino al caso
limite in cui α è zero. È caso limite
poiché il parallelogramma è
degenerato in un segmento
“doppio”. Il modello ci fa intravedere
il caso limite, che si vede meglio col
disegno a lato
•  La somma dei vettori a e b, variabili
in direzione, ma costanti in modulo,
è massima quando:
  α=0° essendo α l’angolo formato dai
due vettori.
  Questo massimo è la somma dei
moduli dei due vettori.
Rappresentazione geometrica del
nostro modello al caso limite
Un altro caso limite: α = 180°
Dall’osservazione del modello, si
ricava che :la somma dei vettori
a e b, variabili in direzione, ma
costanti in modulo, è minima
quando:
  α= 180° essendo α l’angolo
formato dai due vettori;
  Questo minimo è uguale alla
differenza dei moduli.
•  Si legge poco, ma qui c’è scritto il nostro percorso per arrivare
alle conclusioni sulla funzione…
La funzione che esprime la diagonale in
funzione dell’angolo α
• Questa è anche la nostra funzione “somma di due vettori di modulo
costante”. In simboli y=ƒ(α). Riepiloghiamo le sue caratteristiche:
• È una funzione decrescente (*)
• Assume valore massimo quando α = 0°
• Assume valore minimo quando α = 180°
•  (*) Non tutti eravamo convinti che la diagonale crescesse al diminuire
dell’angolo, nonostante l’elastico lo mostrasse con evidenza.
Qualcuno ha cercato una dimostrazione “autorevole”. E questa c’è:
un teorema che ha fatto faticare e che questo modello chiarisce
molto bene.
Se due triangoli hanno due lati rispettivamente uguali e gli angoli fra
essi compresi disuguali, allora all’ angolo maggiore sta opposto il lato
maggiore.
N.B. Il nostro α è il supplementare dell’angolo opposto alla diagonale.
Durante la spiegazione la professoressa è solita
porre delle domande alla classe e farla ragionare
riguardo ai problemi.
I casi sono due: o i ragazzi che capiscono e cercano
di risolvere il problema, parlano alla classe oppure
talvolta capita che debba intervenire la
professoressa stessa data la troppa confusione di
idee nei ragazzi.
•  Anche stavolta in alcuni punti la classe ha avuto delle
incertezze e ci sono stati dei ragazzi che sono
attivamente intervenuti o ponendo i loro dubbi ai
compagni o cercando di risolvere con il modello il
problema posto durante la spiegazione.
“Momenti della discussione”
Il punto della situazione
•  Qualche volta è
stato opportuno che
la professoressa
facesse il punto
della situazione e
spiegasse
l’argomento non
capito dalla maggior
parte della classe..
È molto utile per la classe partecipare alla
discussione sia con l’insegnante sia con i
compagni che meglio hanno capito il tema su
cui si sta lavorando, ma anche con chi,
avendo diversi dubbi, chiede chiarimenti e
pone domande che fanno riflettere e …
progredire.
Classe II E
Insegnante: Laura Gori
Liceo classico Michelangiolo
Firenze