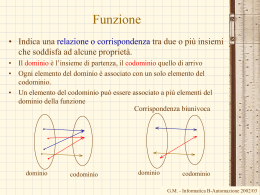
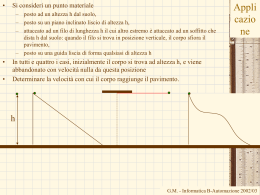
L’energia potenziale della forza di
gravitazione universale - la velocità di fuga
• La forza di gravitazione universale è
conservativa
U
E>0
E=0
U(r)  G
GmM T
RT
r
mM
r
• La velocità di fuga dalla terra:
U
ro
E
E<0
1
GmM T
mv 2 
2
RT
• Per la fuga dalla terra, E>=0:
1
GmM T
mv 2f 
 0  vf 
2
RT
mg 
GmM T
R2T
2GM T
RT
 v f  2gR T 
2 9.81* 6.37 *106  125.0 *106  11.2 *103 m s
G.M. - Informatica B-Automazione 2002/03
Sistemi di particelle
z
•
– Si determinano le forze che agiscono sul
punto materiale
– Si applica la seconda legge di Newton
– Si risolvono le tre equazioni differenziali
per trovare il moto dei punti proiezione
sugli assi (se le equazioni sono
indipendenti)
– Altrimenti si risolve il sistema di tre
equazioni derivanti alla seconda legge di
Newton.
– Si determina così la legge oraria.
•
•
R (1est )
Abbiamo mostrato come è possibile
determinare il moto di un punto materiale
Vediamo ora come si può descrivere il
moto di sistemi più complessi che non
possono essere rappresentati con un punto
materiale.
Studiamo cioè i Sistemi di punti materiali!
F12
P1
F21
r1
F23
F13
r2
P2
F31
R (2est )
y
r3
R (3est )
P3
x
F32
Proviamo ad operare come
abbiamo imparato a fare.
G.M. - Informatica B-Automazione 2002/03
Sistemi di particelle
z
2
d r
m1 21  R1
dt
R (1est )
F12
P1
d 2r2
m2 2  R 2
dt
................
d 2ri
m i 2  Ri
dt
.................
d 2rn
m n 2  Rn
dt
F21
r1
• una volta per ciascun punto facente parte
del sistema
• poi si può risolvere il sistema di 3n
equazioni differenziali che viene fuori.
Molto difficile!!
F13
Ri  risultante delle forze
agenti sulla particella i
Si può scrivere n volte la seconda legge
della dinamica,
F23
r2
P2
F31
R (2est )
y
r3
R (3est )
P3
x
F32
È possibile, rinunciando ad una
descrizione dettagliata del moto delle
singole particelle, ottenere almeno una
descrizione del moto dell’insieme delle
particelle?
G.M. - Informatica B-Automazione 2002/03
Il centro di massa di un sistema di punti
materiali
m r
 m  m  m ....  m ....  m  M
n
n
i i
rCM 
i
i1
n
m
1
2
i
n
i1
i
n
m r 
i1
i i
z
m1r1  m2 r2 ....  mi ri ....  mn rn
i1
n
m x
P1
i i
n
ponendo M 
r1
rCM
r2
P2
i1
M
n
m y
r2
i i
yCM =
n
i1
M
m z
i i
rCM =
i1
n
m r
P3
x
xCM =
i1
y
r3

mi
i i
z CM =
i1
G.M.M
- Informatica B-Automazione 2002/03
M
Il centro di massa del sistema terra-sole
mt
ms
xs
O
x
xt
n
m x
i i
i1
xCM =
n
x CM
M
m y
i i
y CM =
i1
n
M
m z
0
i i
z CM =
•
•
i1
M
0
sxs + m tx t
= mm
s + mt
dove
m s = 2 1030 Kg;
d ts = 1.5 1011 m
m t = 6 1024 Kg
x CM 
m S xS  m T x T  m TxS  m Tx S

mS  mT
d CM S 
mT
d
m S  m T T S
 xS 
m T x T  xS 
mT
 xS 
d TS
mS  mT
mS  mT
d CM T 
mS
d
m S  m T T S
Il centro di massa si trova sul segmento
che congiunge i due punti materiali
È più vicino al punto materiale di massa
maggiore
d CM S 
dCM S m T

d CM T
mS
6x102 4
11
5
1.5x10

4.5x10
m
2x103 0  6x10 2 4
G.M. - Informatica B-Automazione 2002/03
•
Tre masse uguali sono ai vertici di un triangolo equilatero di lato L.
Determinare la posizione del centro di massa
y
3
x CM 
L
1
1 (0,0)
2
2 (L,0)
3 (L cos 60, Lsen 60)
y
2
x
CM12
3 L
m 1y1  m 2y 2  m3 y3 m0  0  L sen60
3L
2




m1  m 2  m3
3m
3
6
Posso determinare prima il centro di massa delle particelle 1 e 2.
m x  m2 x 2
x  x2 L
x CM1 2  1 1

xCM 1 2  1

se
m
m
m1  m 2
2
2
1
2
Calcoliamo ora la posizione del CM della particella 3 e di una
particella di massa 2m posta nella posizione del CM delle
particelle 1 e 2.
L
x

CM
Il centro di massa si troverà sulla congiungente:
2
3
1
m1x1  m2x 2  m3 x3 m0  L  L cos60 1.5  L L



m1  m2  m3
3m
3
2
x
y CM
1
Applic
azione
x
y CM 
2m  0  mL 3 

2 
3m

3 L
3L
2

3
6
G.M. - Informatica B-Automazione 2002/03
Il centro di massa di corpi simmetrici
x1
x CM 
•
m 1x1  m 2x 2
m1  m 2
x
x2

se m1 m 2
xCM 
x1  x2
2
Centro di massa di una sbarra
omogenea
Asse di simmetria
Centro di
simmetria
Centro di massa
di una disco omogeneo
G.M. - Informatica B-Automazione 2002/03
•
L’elemento oscillante di un pendolo è costituito da una sbarretta di massa
ms=0.5kg e lunga 50 cm a cui è attaccata un disco di massa md=1kg di 20cm
di diametro. Determinare la posizione del CM.
y
y
•
•
Applic
azione
CM della sbarra (0,0.45m) ms=0.5kg
CM del Disco (0,0.1m) md=1kg
x CM  0
x
x
m1y1  m2y 2 1kg  0.1m  0.5kg  0.45m 0.1  0.225kgm 0.325
y CM 



m  0.22m
m1  m2
1.5kg
1.5kg
1.5
G.M. - Informatica B-Automazione 2002/03
•
Nella figura si vede una piastra quadrata di lamiera uniforme con lato di 6m,
dalla quale è stato ritagliato un pezzo quadrato di 2 m di lato con centro nel
punto x=2m,y=0m L’origine delle coordinate coincide con il centro della
piastra quadrata. Trovare le coordinate x e y del CM.
y
•
CM
CM2
CM1
•
•
•
x
Applic
azione
Per ragioni di
simmetria
y CM  0
CM Intera piastra (0,0 m) M
CM1 incognito (?,0) m1=(36-4)/36M=8/9M
CM2 (2,0) m2=1/9M
8
1
Mx

Mx 2
1
m 1x1  m 2x 2 9
9
x CM 

0
m1  m 2
M
8
1
x
Mx 1  Mx 2  0  x1   2  0.25m
9
9
8
G.M. - Informatica B-Automazione 2002/03
Il centro di massa di corpi continui
y
dm
r
x
z
n
m r
i i
rCM 
rCM 
i1
n

corp o
mi
 dm x
corp o
 dm
corp o
 dm
corp o
i1
x CM 
 dmr
y CM 
 dm y
corp o
 dm
corp o
z CM 
 dm z
corp o
 dm
corp o
G.M. - Informatica B-Automazione 2002/03
•
Determinare la posizione del centro di massa di un semidisco omogeneo di
massa M e raggio R.
x CM  0 per ragioni di simmetria
y
•
y+dy
y

M
R 2
y CM 
•
q
x
•
2

corp o


dm

4M
cos qydy
R
corp o
M

4
R
 cos qydy
corp o
corp o
y CM 
4R



2
0
cos qsen qdq 
2
Dividiamo il semicerchio in strisce
molte sottili
Sostituiamo ciascuna striscia con il
suo centro di massa (0,y)
Associamo a ciascun CM parziale
la massa dell’intera striscia.
4M
cos qdy
R
 dm  2R cos qdy 
dm y
Applic
azione
y  Rsen q
dy  R cosqdq
y CM 
4
R
 cos qRsen qRcos qdq
corp o

q 2
4R  cos
4R 0 1  4R


  
 .424R


 
3

3
3
3

0
3
G.M. - Informatica B-Automazione 2002/03
z
La velocità del centro
di massa
•
•
•
P1
Se i vari punti materiali si muovono
Anche il centro di massa si muoverà
Calcoliamo la sua velocità
r1
rCM
r2
P2
r2
n
m r
i i
rCM 
m
y
r3
i1
n
P3
i
x
i1
n
 n

dri
m
r
m
i i 
i

n


dt
drCM
d i1
1 d
i1
v CM 
 
 m r  

 
dt
dt
M
M dt  i1 i i 
M


per defin izion e
perchè la deriv ata si p uò
distribuire sulla so mma


e perchè m è costan te



n
m v
i i
i1
M
i
1
perchè
è costan te
M
G.M. - Informatica B-Automazione 2002/03
z
L’accelerazione del
centro di massa
•
P1
Possiamo anche calcolarci
l’accelerazione del centro di massa
r1
rCM
r2
P2
r2
n
m v
i i
v CM 
y
r3
i1
M
P3
x
a CM 
dv CM
dt
per defin izion e
n
 n

dvi
m
v
m
i i 
i

n


dt
d i1
1 d
i1
 
 m v  

 
dt
M
M dt  i1 i i 
M


perchè la deriv ata si p uò
distribuire sulla so mma


e perchè m è costan te



n
m a
i i
i1
M
i
1
perchè
è co stan te
M
G.M. - Informatica B-Automazione 2002/03
•
Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il verde
(t=0s) parte con una accelerazione costante di 4 m/s2. Nello stesso istante
sopraggiunge con velocità costante di 8m/s un camion di massa 2000kg che
sorpassa l’auto. A che distanza dal semaforo si troverà il centro di massa del
sistema auto camion per t=3.0s?
x C  vC t  x C  24m
Quale sarà la sua velocità?
t3s
t=0
xa 
x
O
t=3s
O
x
x CM (3s) 
1 2
at
2
v C  vC
v a  at

t3s
x a  18m

v C  8m / s

va  12m / s
t 3s
t 3s
Applic
azione
m C x C  m a x a 2000  24  1000  18

m  22m
mC  ma
3000
m C v C  m a va 2000  8  1000  12 m
m

 9.3
mC  ma
3000
s
s
m a  ma a a 2000  0  1000  4 m
m
a CM (3s)  C C


1.33
mC  m a
3000 B-Automazione
s2 2002/03
s2
G.M. - Informatica
v CM (3s) 
•
Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il verde
(t=0s) parte con una accelerazione costante di 4 m/s2. Nello stesso istante
sopraggiunge con velocità costante di 8m/s un camion di massa 2000kg che
sorpassa l’auto. A che distanza dal semaforo si troverà il centro di massa del
sistema auto camion per t=3.0s?
Quale sarà la sua velocità?
Applic
azione
t=0
x
O
x CM (0s)  0m
m C vC  ma va 2000  8  1000  0 m
m
v CM (0s) 

 5.33
mC  m a
3000
s
s
a CM (0s) 
1
x CM  v CM t  a CM t 2
2
v CM (t)  v CM (0s)  at

t3s

t3s
m C a C  m a a a 2000  0  1000  4 m
m


1.3
mC  ma
3000
s2
s2
1
xCM  5.33  3  1.33  9  22.0m
2
vCM (3s)  5.33  1.33x3  9.33m / s
G.M. - Informatica B-Automazione 2002/03
z
Ricapitoliamo
n
m r
m x
i i
rCM =
P1
n
i i
i1
x CM =
M
r1
i1
n
rCM
r2
M
m y
i i
y CM =
i
z CM =
n
x
M
n
m v
i i
M
P3
i1
n
m v
i1
y
r3
i i
i1
v CM =
M
m z
n
m
r2
i1
n
con M 
P2
m a
i xi
vx CM =
i1
n
m a
i i
a CM =
M
n
i1
M
i xi
a xCM =
n
m v
i1
n
i yi
a yCM =
M
M
M
m a
i zi
i1
i1
n
m v
v z CM =
M
m a
i yi
vy CM =
i1
i zi
a z CM =
i1
G.M. - Informatica B-Automazione 2002/03
M
Il teorema del centro di massa
z
n
MaCM =

dalla definizione di
accelerazione del CM
m i ai
R (1est )
i1
mi a i  Ri
Ri  R i
( est)

F12
P1
i  1,2,..., n
f
ij
F21
r1
F13
rCM
r2
i  1,2,...,n
ji
•
– Le forze dovute alle altre particelle
che fanno parte del sistema di punti
materiali
•
r2
P2
R (2est )
F31
Forze interne
MaCM =
y
r3
R (3est )
P3
x
Forze esterne
– Le forze dovute alle altre particelle
che non fanno parte del sistema di
punti materiali
F23
n

i1
n
m i ai 

i1
F32

( est)
Ri 


ji

fij  

n

i1
n
R(est)

i
 f
ij
i1 ji
perchè in un a somma è po ssibile cambiareordin
l' e degli addendi
G.M. - Informatica B-Automazione 2002/03
Il teorema del centro di massa
z
n
R
(est)
i
R (1est )
Risultante delle forze esterne
i1
 f
ij
i1 ji
•
F12
P1
n
Risultante delle forze interne
F21
r1
F13
rCM
r2
La risultante delle forze interne è
nulla
– Le forze interne sono a coppia
r2
F31
fij  fji
F23
P2
R (2est )
y
r3
– Ogni coppia ha risultante nulla
– La risultante è la somma di tanti
termini tutti nulli
R (3est )
P3
x
F32
3
 f
ij
i1 ji
 f1 2  f1 3  f2 1  f2 3  f3 1  f3 2  f1 2  f2 1  f1 3  f3 1  f2 3  f3 2  0
i1
i2
i3
0
0
0
– Il caso di n=3
G.M. - Informatica B-Automazione 2002/03
Il teorema del centro di massa
z
( est)
MaCM = R
•
•
•
•
•
R (1est )
F21
r1
il centro di massa si muove come un
punto materiale, avente una massa pari
alla massa totale del sistema, sottoposto
all'azione della risultante delle sole forze
esterne agenti sul sistema.
I singoli punti possono avere un moto
complicato
Il moto del centro di massa è influenzato
dalle sole forze esterne
Il moto del centro di massa rappresenta il
moto di insieme del sistema
•
F12
P1
L’accelerazione del centro di massa
è dovuta alle sole forze esterne.
F13
rCM
r2
F23
r2
F31
P2
R (2est )
y
r3
R (3est )
P3
x
F32
Il moto dell’automobile è determinato dalle forze esterne: la
forza peso, la normale esercitata dall’asfalto, la forza di attrito
G.M. -passiva
Informatica
B-Automazione
esercitata dall’asfalto, la resistenza
offerta
dall’aria2002/03