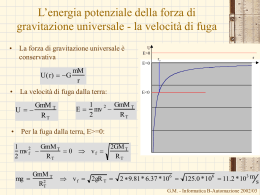
•
Si consideri un punto materiale
– posto ad un altezza h dal suolo,
– posto su un piano inclinato liscio di altezza h,
– attaccato ad un filo di lunghezza h il cui altro estremo è attaccato ad un soffitto che
dista h dal suolo: quando il filo si trova in posizione verticale, il corpo sfiora il
pavimento,
– posto su una guida liscia di forma qualsiasi di altezza h
•
•
Appli
cazio
ne
In tutti e quattro i casi, inizialmente il corpo si trova ad altezza h, e viene
abbandonato con velocità nulla da questa posizione
Determinare la velocità con cui il corpo raggiunge il pavimento.
h
G.M. - Informatica B-Automazione 2002/03
•
Nel primo caso
– Agisce solo la forza peso (che è conservativa)
– Posso applicare la conservazione dell’energia
h
Appli
cazio
ne
E  0  Ei  Ef
K i  Ui  K f  Uf
Ki  0
U i  mgh
K f  12 mv 2f
Uf  0
Abbiamo scelto il pavimento come
punto di riferimento ed assegnato
al pavimento energia potenziale
nulla
0  mgh  12 mv 2f  0
v f  2gh
L’energia potenziale iniziale viene
trasformata in energia cinetica
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
Nel secondo caso agiscono
– Sia la forza peso, che è conservativa,
– E la reazione vincolare del piano inclinato,
• Solo la componente normale, perché per ipotesi il piano è liscio
•
Possiamo applicare la relazione lavoro energia:
E  Wnc
N
h
 Wnc  WN
La normale è perpendicolare allo
spostamento: quindi il suo lavoro è nullo
P
E  Wnc  0  E i  Ef
Si ritorna la caso precedente
0  mgh 
1
2
mv 2f
0
K i  Ui  K f  Uf
v f  2gh
Ki  0
U i  mgh
K f  12 mv 2f
Uf  0
La velocità finale è la stessa del caso precedente
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
Nel terzo caso agiscono
– Sia la forza peso, che è conservativa,
– E la tensione nella corda.
•
h
Possiamo applicare la relazione lavoro energia:
T
E  Wn c  Wn c  WT
dWT  T  dr  0
dr
perchè Tdr
P
Il lavoro infinitesimo fatto dalla tensione
E  Wnc  0  E i  Ef
T è nullo, ma anche il lavoro complessivo
Si ritorna la caso precedente
K i  Ui  K f  Uf
Ki  0
U i  mgh
K f  12 mv 2f
0  mgh  12 mv 2f  0
v f  2gh
Uf  0
La velocità finale è la stessa del caso precedente
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
Nell’ultimo caso agiscono
– Sia la forza peso, che è conservativa,
– E la reazione vincolare della guida,
• Solo la componente normale, perché per ipotesi la guida è liscia
•
Possiamo applicare la relazione lavoro energia:
E  Wnc
 Wnc  WN
dWN  N  dr  0
N
h
perchè Ndr
dr
P
Il lavoro infinitesimo fatto dalla Normale
N è nullo, ma anche il lavoro complessivo
E  Wnc  0  E i  Ef
K i  Ui  K f  Uf
Si ritorna la caso precedente
0  mgh  12 mv 2f  0
v f  2gh
Ki  0
U i  mgh
K f  12 mv 2f
Uf  0
Conclusione: la velocità finale è sempre la
stessa in tutti e quattro i casi esaminati.
G.M. - Informatica B-Automazione 2002/03
Consigli sull’uso della conservazione
dell’energia nella risoluzione dei problemi
• Utilizzare la conservazione dell’energia ogni volta che è possibile
(quando non è richiesto di determinare intervalli di tempo o trovare
funzioni del tempo (legge oraria))
– L’approccio energetico è più semplice della seconda legge della dinamica:
• la conservazione dell’energia è un’equazione scalare mentre le seconda legge
di Newton è vettoriale corrispondente a ben tre equazioni scalari
• la seconda legge di Newton è un’equazione differenziale del secondo ordine, la
conservazione dell’energia è solo del primo ordine.
• Introdurre un sistema di riferimento inerziale
• Individuare tutte le forze agenti sul punto materiale o sui punti materiali
– Ricercare i corpi dell’ambiente circostante che possono esercitare
forze
• Tener presente che alcune forze agiscono a distanza
• Altre agiscono per contatto
– Attenzione ai corpi a contatto
G.M. - Informatica B-Automazione 2002/03
Consigli sull’uso della conservazione
dell’energia nella risoluzione dei problemi
• Separare le forze tra forze conservative e forze non conservative.
• le forze conservative
– Forza peso
Ux, y, z  mgy  mgh
– Forza elastica
U(x, y,z) 
1 2
kx
2
Ux, y, z  
– Forza di gravitazione universale
– Forza di Coulomb
h = quota
Ux, y, z 
GmM
r
1 q1q 2
4 o r
• Tutte le altre forze vanno considerate non conservative
• Scrivere l’equazione della conservazione dell’energia meccanica
totale.
–
–
E = 0 se tutte le forze sono conservative
E = Wnc se non tutte le forze sono conservative
G.M. - Informatica B-Automazione 2002/03
Consigli sull’uso della conservazione
dell’energia nella risoluzione dei problemi
• Scegliere l’istante iniziale e quello finale tra cui valutare la
conservazione dell’energia
– Ottimizzate i calcoli e la precisione del risultato
– Partite sempre istanti iniziali e finali i cui dati sono derivabili dalla traccia.
• Valutare il lavoro delle forze non conservative (se presenti)
–
–
–
–
La forza di attrito statico non fa lavoro
La forza di attrito dinamico fa sempre un lavoro negativo
La Normale compie lavoro nullo perché perpendicolare allo spostamento
La tensione nelle corde con uno dei capi fissi compie lavoro nullo (caso
del pendolo)
– Il lavoro complessivo delle tensioni ai due capi di una corda ideale è nullo
• Ad un capo la forza e lo spostamento sono concordi (lavoro positivo)
• All’altro capo sono discordi (lavoro negativo)
• Nelle corde ideali le forze ai due capi della corda sono uguali così come gli
spostamenti dei due capi.
G.M. - Informatica B-Automazione 2002/03
Consigli sull’uso della conservazione
dell’energia nella risoluzione dei problemi
• Valutare l’energia cinetica e potenziali negli stati selezionati come
iniziale e finale.
– Per calcolare l’energia potenziale occorre fissare il punto di riferimento
(arbitrariamente) a cui assegnare un valore arbitrario dell’energia
potenziale (solitamente il valore zero).
– Mi raccomando: il punto di riferimento e il valore arbitrario assegnato
all’energia potenziale del punto di riferimento deve essere lo stesso sia nel
calcolo delle quantità iniziali che per quelle finali.
G.M. - Informatica B-Automazione 2002/03
•
Un blocco di massa M=100kg è trascinato a velocità costante di 5 m/s su di un
pavimento orizzontale da una forza di 122 N diretta con un angolo di 37° al di
sopra del piano orizzontale. Qual è la potenza con cui la forza applicata produce
lavoro sul blocco?
•
Qual è il valore
Appli
cazio
ne
• della forza di attrito tra il blocco ed il piano?
• e del coefficiente di attrito dinamico?
•
Quale valore deve avere la forza da applicare per far muovere il blocco a
velocità costante, sempre 5 m/s) se esso viene spinto da una forza diretta a 37°
verso il basso? Quale potenza deve essere fornita in questo caso?
37°
37°
G.M. - Informatica B-Automazione 2002/03
•
•
Un blocco di massa 3.5 kg è spinto via da una molla compressa avente costante
elastica 600 N/m. Dopo essersi staccato dalla molla, una volta che essa ha
raggiunto la posizione di riposo, il blocco viaggia sulla superficie orizzontale
con coefficiente di attrito dinamico 0.25 fino a fermarsi alla distanza di 7.8 m.
Quanta energia meccanica è stata dissipata in energia termica dalla forza di
attrito per far arrestare il blocco? Qual è la massima energia cinetica del blocco?
Di quanto era compressa la molla inizialmente?
Appli
cazio
ne
G.M. - Informatica B-Automazione 2002/03
•
•
•
Un pattinatore di massa m = 52 kg sta ruotando su una circonferenza di raggio
r=20 m ad una velocità di 3 m/s. Egli si mantiene su questa traiettoria reggendo
una fune attaccata mediante un cuscinetto privo di attrito ad un palo posto al
centro del cerchio.
Calcolare la tensione T esercitata dalla fune.
Il ghiaccio su cui egli pattina può essere considerato privo di attrito, ma per una
parte del moto attraversa una pozza sabbiosa di lunghezza 48 cm dove il
coefficiente di attrito è m = 0.10. Quanto vale la velocità subito dopo aver
attraversato la pozza sabbiosa? Quanto deve valere la tensione nella fune
affinché continui a percorrere la stessa traiettoria dopo aver attraversato la pozza
sabbiosa?
Vista dall’alto
Appli
cazio
ne
Vista laterale
G.M. - Informatica B-Automazione 2002/03
•
•
Appli
cazio
ne
Un corpo di massa m = 2 kg viene lanciato con una velocità di 3 m/s su di un
piano inclinato di 20° scabro con coefficienti di attrito statico e dinamico
rispettivamente di 0.4 e 0.3.
Determinare:
• la distanza percorsa dal corpo lungo il piano inclinato prima di fermarsi.
• il tempo impiegato.
•
Stabilire se il corpo resta nella posizione in cui si è fermato o se ridiscende lungo
il piano inclinato. In questo ultimo caso determinare la velocità con cui arriva
alla base del piano inclinato.
v
=20°
G.M. - Informatica B-Automazione 2002/03