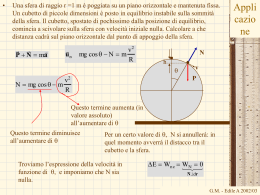
•
Una sfera di raggio r =1 m è poggiata su un piano orizzontale e mantenuta fissa.
Un cubetto di piccole dimensioni è posto in equilibrio instabile sulla sommità
della sfera. Il cubetto, spostato di pochissimo dalla posizione di equilibrio,
comincia a scivolare sulla sfera con velocità iniziale nulla. Calcolare a che
distanza cadrà sul piano orizzontale dal punto di appoggio della sfera.
P  N  ma
un
v2
mg cos q  N  m
R
Appli
cazio
ne
N
h
q
v
P
v2
N  mg cos q  m
R
Questo termine aumenta (in
valore assoluto)
all’aumentare di q
Questo termine diminuisce
all’aumentare di q
Per un certo valore di q, N si annullerà: in
quel momento avverrà il distacco tra il
cubetto e la sfera.
Troviamo l’espressione della velocità in
funzione di q, e imponiamo che N sia
nulla.
E  Wn c  WN  0
Ndr
G.M. - Informatica B-Automazione 2002/03
Poniamo l’energia potenziale uguale a zero
quando il cubetto si trova alla sommità della
sfera.
Ef  Ei
Appli
cazio
ne
K f  Uf  K i  Ui
1
2
mv 2f  mgh  0  0
h  R 1 cos q
h
q
v 2 q  2gR 1  cosq
N  mg cosq  m
y
N
v
P
2gR 1  cosq
 mg 3cosq  2
R
x
La normale N si annullerà quando
3cos qd  2   0
ossia
cos qd 
Il distacco avverrà nel punto:
2
3
senq d  1  cos2 q d  1
4
9

5
9

5
3
5
R  .74m
3
5
y d  R  R cos qd  R  1.67m
3 G.M. - Informatica B-Automazione 2002/03
x d  Rsen qd 
Appli
cazio
ne
La velocità al momento del distacco
2
2

v 2 q  2gR 1  cos q  2gR  1    gR
3
3
2
gR
3
 vd 
Le cui componenti x e y valgono
y
2 2
v xd  vd cos q d 
gR  1.70 ms
3 3
5 2
v yd  v d senq d  
gR  1.90 ms
3 3
Il moto dopo il distacco avverrà sotto la
sola azione della forza peso (moto del
proiettile)
P  ma
x : 0  ma x
y :  mg  ma y
L’istante in cui il cubetto impatta
al suolo si ottiene imponendo y=0.
t 1  0.42s
t 1  0.81s
h
q
N
v
P
x
x  x d  vxd t
Facendo ripartire il cronometro
2
y  y d  vyd t  12 gt nel momento del distacco.
y d  v y dt  12 gt  0 t 
2
v y d  v 2y d  2gy d
g
x  x d  vx dt  .74 1.70  .42 1.45m
G.M. - Informatica B-Automazione 2002/03
•
Un blocchetto di massa m può scorrere lungo una pista, priva di attrito, a spirale
mostrata in figura.
Da quale altezza sopra il punto più basso si dovrebbe lasciar cadere il blocchetto
(con velocità iniziale nulla), per far si che riesca a fare un il giro completo del
“ricciolo”?
Quanto vale la forza complessiva agente sul blocchetto quando passa per il
punto Q della figura?
P  N  ma
un
Appli
cazio
ne
v2
mg cos q  N  m
R
v2
N  m  mg cos q
R
Affinché ci sia il contatto occorre che N sia sempre
maggiore di zero
Il punto più delicato è la sommità del ricciolo in
quanto in quella posizione
• v è minima
• Mentre il secondo termine diventa in modulo uguale a
mg
Occorre quindi imporre che N sia al massimo nulla al
vertice del ricciolo: imporre cioè che, in quella
posizione, la forza centripeta sia fornita dalla sola
forza peso
q
N
P
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
La velocità alla sommità del ricciolo deve quindi essere almeno:
v2
N  0  0  m  mg
R
 v 2  gR
Imponendo la relazione lavoro-energia tra il punto di partenza, ad altezza h e la
sommità del ricciolo, si ottiene
E  Wn c  WN  0
Ef  Ei
Ndr
K f  Uf  K i  Ui
1
2
mv 2f  mg2R  0  mgh
v 2f  2gh  2R
Tenendo conto del limite minimo su v, si ottiene:
R
5
 2R  R
2
2
5
2
1
La velocità in Q: 2 mv Q  mgR  0  mg R
2
gR  2gh  2R
v 2Q

N
h
 5gR  2gR  3gR
P
RPN
P  mg
v2
3gR
Nm m
 3mg
R
R
G.M. - Informatica B-Automazione 2002/03
•
Due bambini stanno facendo una gara a chi riesce a centrare una scatoletta sul
pavimento con una biglia sparata da una pistola a molla, montata su un tavolo
orizzontale. Come si vede dalla figura, il bersaglio è piazzato a 2.20 m in
orizzontale dal bordo del tavolo. Orazio comprime la molla di 1.10 cm, ma il suo
tiro risulta corto di 27 cm.
Di quanto deve comprimerla Giustina per fare centro? Ignorate gli attriti.
Appli
cazio
ne
La biglia una volta rilasciata dalla molla
ed abbandonato il tavolo si muove sotto
l’azione della sola forza peso (moto del
proiettile).
Se si comincia a contare il tempo nel
momento in cui la biglia abbandona il
tavolo, le condizioni iniziali sono
xo=0,
yo=h
vxo=?
vyo=0
vxo è la velocità con cui la biglia
abbandona la molla
La legge oraria sarà:
x  v o xt
1
y  h  gt 2
2
Indichiamo con t l’intervallo di
tempo impiegato per cadere.
Il percorso orizzontale effettuato
sarà:
d1  vox1t
G.M. - Informatica B-Automazione 2002/03
•
Dato che il primo lancio è corto, occorre aumentare la velocità vxo affinchè la
biglia colpisca il bersaglio:
d 2  vox2 t
•
Dividendo membro a membro si ottiene:
d 2 vox 2

d1 vox1
 v ox2  v ox1
Appli
cazio
ne
d2
d1
La velocità vxo1 è la velocità acquistata
dalla biglia er una compressione di 1,1 cm
della molla. Quale deve essere la
compressione della molla per ottenere la
velocità vxo2 che ci consentirà di colpire il
bersaglio?
Determiniamo la relazione tra
compressione e velocità orizzontale della
biglia.
Durante l’espansione della molla, la biglia
è sottoposta alla forza elastica, alla forza
peso e alla Normale.
Le ultime due forze compiono lavoro
nullo, la forza elastica è conservativa.
Si conserva l’energia meccanca
E  Wn c  0
totale
1 2 1 2
kx  mv
2 1 2 x o1
1 2 1 2
kx2  mv x o2
2
2
x 2  x1
x12 v 2xo1 d21
 2
2  2
x 2 vxo 2 d2
d2
2.20
 1.1cm
 1.25cm
d1
2.20

27.0
G.M. - Informatica B-Automazione 2002/03
•
Tarzan, che pesa 688 N, salta da una roccia appeso ad una provvidenziale liana
lunga 18 m (vedi figura). Dall’alto della roccia al punto più basso della sua
oscillazione cala di 3.2 m. La liana è soggetta a rompersi se la tensione supera
950 N.
Determinare se la fune si romperà
Se sì, determinare l’angolo rispetto alla verticale a cui avviene la rottura
Se no, determinare il suo valore massimo.
Appli
cazio
ne
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
Un blocco di legno da 0.520 kg è saldamente attaccato ad una leggerissima
molla orizzontale (k=180 N/m), ed è appoggiato su un tavolo orizzontale come
mostrato in figura.
Il blocco viene spostato in maniera da comprimere la molla di 5.0 cm e quindi
rilasciato con velocità nulla. Si osserva che il blocco supera la posizione di
equilibrio di 2.3 cm prima di fermarsi per poi tornare indietro. Determinare il
coefficiente di attrito tra il tavolo ed il blocco di legno.
k
m
O
G.M. - Informatica B-Automazione 2002/03
•
Le due masse mostrate in figura inizialmente sono poste ciascuna a 1.80 m dal
suolo e la carrucola, priva di massa e di attrito, è a 4.80 m dal suolo. Qual è
l’altezza massima raggiunta dal corpo più leggero una volta che il sistema viene
lasciato libero di muoversi?
Appli
cazio
ne
4,80 m
2,2 kg
3,2 kg
1,80 m
G.M. - Informatica B-Automazione 2002/03
•
Una particella di massa m= 50g scivola all’interno di una ciotola la cui sezione
ha archi circolari su ciascun fianco ed una parte centrale orizzontale piatta tra i
punti a e b di larghezza 20 cm. Le parti curve sono prive di attriti mentre per la
parte piatta il coefficiente di attrito dinamico è mk= 0,15. L particella è rilasciata
a riposo sul bordo della ciotola che è 10 cm al di sopra della parte piatta.
Appli
cazio
ne
• Qual è la velocità in a?
• Quella in b?
•
Dove si fermerà alla fine la particella?
10 cm
a 20 cm b
G.M. - Informatica B-Automazione 2002/03
•
Un blocco di 3.22 kg scivola lungo un piano inclinato di 28.0° e privo di attrito
e, dopo avere percorso una distanza d, comprime una molla per 21.4 cm per poi
arrestarsi momentaneamente. La costante elastica della molla è di 427 N/m.
– Quanto misura d?
•
Dopo aver compresso la molla, il blocco aumenta la sua velocità prima di
iniziare a decelerare nuovamente. Quale distanza percorre prima di raggiungere
la sua massima velocità e cominciare a rallentare?
Appli
cazio
ne
G.M. - Informatica B-Automazione 2002/03