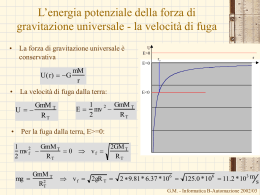
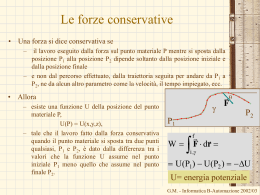
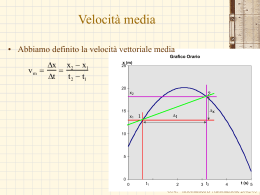
Riassunto della prima lezione
• La fisica è una scienza sperimentale! E’ necessario misurare le
grandezze fisiche.
• Ogni volta che si fa una misura si commettono errori (casuali e
sistematici).
• Attenzione alla propagazione degli errori: in una somma o differenza
l’errore assoluto del risultato non può essere più piccolo del più grande degli
errori di partenza, in un prodotto o divisione l’errore relativo del risultato non
può essere più piccolo del più grande degli errori di partenza.
• Campioni e metodi di misura fissati da accordi internazionali.
• Noi usiamo il SI (7 unità fondamentali, tutte le altre derivate).
• La scelta dei campioni è una questione delicata, da essi dipende la
precisione delle misure.
• Sottolineato l’evoluzione dei campioni del metro e del secondo, sempre
più precisi e sempre più accessibili ed invariabili
G.M. - Informatica B-Automazione 2002/03
Grandezze derivate - Dimensioni
• Le unità di misura di tutte le altre grandezze fisiche sono derivate da
quelle fondamentali attraverso le relazioni che legano ciascuna
grandezza a quelle fondamentali.
• Per esempio la relazione che lega la velocità allo spazio percorso ed al
tempo impiegato è data da
d
v
Dt
• Si dice anche che la velocità ha le dimensioni di una lunghezza diviso
un tempo ([v]=[d][Dt]-1 =[L][T]-1 equazione dimensionale)
• Per “dimensioni” si intendono gli esponenti a cui bisogna elevare le
grandezze fondamentali per ottenere la grandezza in esame.
• L’unità di misura della velocità sarà (SI): m/s (metri al secondo)
• Il campione della velocità è la velocità di quell’oggetto che percorre un
metro in un secondo.
• NB: la distinzione tra grandezze fondamentali e grandezze derivate è
del tutto arbitraria, è solo una questione di scelta.
G.M. - Informatica B-Automazione 2002/03
L’accelerazione
• Tra le prestazioni di una automobile, viene citato il tempo necessario
per far passare la velocità della vettura da 0 a 100 Km/h, per vetture
sportive questo tempo è al di sotto dei 10 s.
• L'accelerazione è una misura della rapidità con cui cambia la velocità.
Dv vf  v i
Essa è definita come:
a
Dt

tf  t i
 
 
• Le dimensioni sono: a  v T
 L T
• Nel SI l'accelerazione si misura in metri al secondo al quadrato
1
2
m
s2
• Nel caso di una vettura che passa da 0 a 100 Km/h in 10 s,
l'accelerazione media è:
100km  100  1000m 
Dv  1h   3600s 
m
a


 2.78 2
Dt
10s
10s
s
G.M. - Informatica B-Automazione 2002/03
Grandezze derivate dalla lunghezza:
aree, volumi e angoli
• aree
• Triangolo: 1/2 base x altezza
• Parallelogramma: base x altezza
• Cerchio: p x raggio al quadrato
– Le dimensioni
[S] = [L2]
– L’unità di misura il m2.
– Il campione: un quadrato di lato 1 m.
• Volumi
• Parallelepipedo:Area di base x altezza
• Sfera: 4/3 p x raggio al cubo
– Le dimensioni
[V] = [L3]
– L’unità di misura il m3.
– Il campione: un cubo di spigolo 1 m.
G.M. - Informatica B-Automazione 2002/03
Angolo piano
• L’angolo

lunghezza dell' arco
raggio della circonferenza

r
• Le dimensioni


    L L1  L0 
r
y
– L’angolo è un numero puro
(radiante)
2pr
• L’angolo giro: 
 2p (rad)
r
• Fattore di
conversione:
r

x
360 : 2p = gradi :  radianti
360 : 2p = gradi : 1rad  gradi
360  1

 57.35
2p
G.M. - Informatica B-Automazione 2002/03
Angolo solido
area della calotta
S
• L’angolo solido   raggio della sfera al quadrato  r 2
• Le dimensioni
– È un numero puro
(steradiante).
 
S

r2
 
 L 2L 2  L0

• L’angolo solido totale
area della sfera
tot 

raggio della sfera al quadrato
S
r
4pr 2
 2  4p (sr,steradianti)
r
G.M. - Informatica B-Automazione 2002/03
Grandezze derivate dal tempo:
Frequenza
• La frequenza si riferisce ad un fenomeno periodico
numero di cicli
e si definisce come:
f
Dt
• Poiché il numero di cicli è un numero privo di
dimensioni, si dirà che la frequenza ha le
dimensioni di un tempo alla meno uno ( [f]=[T]-1)
e si misurerà in cicli al secondo (s-1).
• Questa unità nel SI si chiama hertz (Hz)
• Se l’intervallo Dt è uguale ad un periodo (T) allora
il numero dei cicli è
numero di cicli 1
f

uguale a 1, pertanto
Dt
T
G.M. - Informatica B-Automazione 2002/03
Alcuni motori di vetture di formula 1 raggiungono 18000 giri al minuto.
Con che frequenza gira l’albero motore?
Qual è l’angolo percorso in un secondo da un punto sulla periferia
dell’albero motore?
Quanto dura un giro?
Applicazione
numero di cicli
18000
f

passando ad unità del SI
Dt
1 min
18000
f
 300 s-1  300 Hz
60s
1 giro = 2p rad
2p rad
 =300giri
 600p rad
giro
1
1
T 
1  0.0033 s = 3.3 ms
f 300 s
G.M. - Informatica B-Automazione 2002/03
Densità o massa volumica
• Si definisce densità di un corpo il seguente
m
rapporto:

V
questa è la densità media
3



M

L

• le cui dimensioni sono:
• e si misura in Kg/m3
Dm
 
Dm
(P) 
DV
con DV molto piccolo (tendente a zero).
DV
G.M. - Informatica B-Automazione 2002/03
Tabella di densità
G.M. - Informatica B-Automazione 2002/03
Densità superficiale e densità lineare
• A volte i corpi si presentano con una delle dimensioni
uniforme e molto più piccola delle altre due (un foglio di
carta, una lastra di ferro, etc.). In tal caso si parla di densità
superficiale:
m
  s 
• Le dimensioni sono:
• e si misura, nel SI, kg/m2.
S
  ML
2

• Se il corpo presenta un aspetto filiforme, si parla di
m
densità lineare:
 
• Le dimensioni sono
• e si misura in kg/m.
 
1



M

L

G.M. - Informatica B-Automazione 2002/03
L’oro che ha un massa di 19.32 g per ogni centimetro cubo di volume, è il
materiale più duttile: può essere steso in fogli sottilissimi o tirato in lunghe
fibre.
a) se si stende in un foglio di 1.000 mm di spessore la massa di 27.63 g,
quale sarà l’area del foglio risultante? E la densità superficiale?
b) Se invece si tira la stessa quantità in una fibra cilindrica di 2.500 mm di
raggio, quale sarà la sua lunghezza? E la densità lineare.
Applicazione
m 19.32g
g


19.32
3
cm
V
1cm 3
passando ad unità del SI

  19.32 g
10 3 kg
3 kg

19.32

19.32x10
cm 3
106 m 3
m3
Troviamo il volume V occupato da una massa pari a 27.63g
m

V
m 27.63x10 -3 kg
 V 
 1.430x10 6 m3
 19.32x10 3 kg
m3
6
3
V 1.430x10 m
2
ma il volume V = Ah  A = 

1.430m
h 1.000x106 m
G.M. - Informatica B-Automazione 2002/03
Applicazione
La densità superficiale della lastra così ottenuta
:
m 27.63x103 kg
3 kg
s  

19.32x10
m2
A
1.430m2
Nel caso del filo il volome V

1.430x106 m 3

3.141x 2.500x10 6
 

1.430x106 m 3
3


72.84x10
m
2 2
1 2 2
3.141x6.250x10 m
m

La densità lineare del filo vale
m
=S
V 1.430x106 m 3
 
S
pR 2
:
27.63x10 3 kg
6 kg


.3793x10
m
72.84x10 3 m
G.M. - Informatica B-Automazione 2002/03
Alcune grandezze fisiche
Grandezza
Area
Volume
Densità
Definizione
Unità di misura
A=base per altezza
metri quadri
m2
V=area di base per altezza
metri cubi
m3
=massa diviso volume occupato
kilogrammi per
metro cubo
metri al secondo
kg/ m 3
metri al secondo
quadrato
newton
m/s2
N
kg m/s2
P=(forza normale)/area
pascal
Pa
N/ m2
Lavoro=forza per spostamento
joule
J
Nm
K= 1/2 massa per velocità al quadrato joule
J
Nm
P=(lavoro effettuato)/(tempo
impiegato)
p=massa per velocità
watt
W
J/s
kilogrammi per
metri al secondo
kg m/s
M=r x F (erre vettor F) prodotto
vettoriale tra il vettore posizione e
laForza
Nm
v=(Distanza percorsa)/(tempo
impiegato)
Accelerazione a=(Variazione di velocità)/(tempo
impiegato)
F=massa per accelerazione
Forza
Velocità
Pressione
Lavoro
Energia
cinetica
Potenza
Quantità di
moto
Momento di
una forza
m/s
G.M. - Informatica B-Automazione 2002/03
Relazioni tra grandezze
F  ma
Entrambi i membri devono avere
le stesse dimensioni
MLT 2  F
ma   ML T 2
Se la relazione contiene la somma di più termini, tutti i
termini devono avere le stesse dimensioni
1 2
x  x o  v o t  at
2
x o posizione iniziale
v o velocità iniziale
a accelerazione
x   L
x o   L 
v o t   LT 1 T  L
1 a t 2  LT 2 T 2  L
  
o
2

G.M. - Informatica B-Automazione 2002/03
Unità di misura nelle relazioni fisiche
• Le unità di misura possono essere usate come un qualsiasi
altro termine nell’equazione algebrica
– Determinare la distanza x dall’origine al tempo t=5 s sapendo che
la distanza dall’origine all’istante iniziale è 5 m, la velocità iniziale
è 4 m/s, l’accelerazione costante è di 2 m/s2.
1
x  x o  v o t  at 2
2
xo = 5 m
v o = 4 m/s
a
m
1 m
x  5m  4 5s  2 2 25s2 
s
2 s
 5m  20m  25m  50m
= 2 m/s 2
G.M. - Informatica B-Automazione 2002/03
Cambiamento di unità di misura
Equazioni dimensionali
• Esprimere la velocità di 110 km/h in unità del sistema
SI.
– 1km=1000m
– 1h = 3600 s
110
km
1km
1000m
m
 110
 110
 30, 5
h
1h
3600s
s
• Quanto tempo impiega un corpo di massa m a cadere
da un’altezza h?
• Dt=khxmygz
[T]=[k][L]x[m]y[LT-2]z=[Lx+zmyT-2z]
1  2z
z   12
0y
y0
0  x  z x   z  12
1
2
Dt  h g

1
2
La verità

h
g
2h
Dt 
g
G.M. - Informatica B-Automazione 2002/03
Una sferetta P viene posta in una conca semisferica di raggio R in un punto
diverso da quello più basso.
La sferetta rotola e l’angolo  indicato in figura varia con la legge:
t 
Applicazione
S
cos(wt)
R
Quali sono le dimensioni di w e S? Qual è l’interpretazione geometrica di S?
R
P

L’argomento della funzione coseno è un angolo, cioè una grandezza
adimensionale. wt deve essere adimensionale.
[wt]= [w] [T]= [T0]
Risulta
[w] = [T1]
L’angolo non ha dimensioni: pertanto [S] [R-1][cos]=[L0M0T0]
La funzione coseno è adimensionale, il raggio R ha le dimensioni di
lunghezza [R]=[L]. Pertanto:
[S]=[L]
S è l’arco di cerchio tra P e il punto più basso della conca.
G.M. - Informatica B-Automazione 2002/03