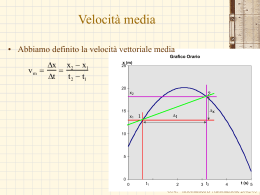
Funzione
• Indica una relazione o corrispondenza tra due o più insiemi
che soddisfa ad alcune proprietà.
• Il dominio è l’insieme di partenza, il codominio quello di arrivo
• Ogni elemento del dominio è associato con un solo elemento del
codominio.
• Un elemento del codominio può essere associato a più elementi del
dominio della funzione
Corrispondenza biunivoca
dominio
codominio
dominio
codominio
G.M. - Informatica B-Automazione 2002/03
Funzione
• Le funzioni più semplici sono quelle che mettono in
relazione due soli insiemi
– In genere noi useremo funzioni che mettono in relazioni due
insiemi di numeri reali o parti di essi.
– Si indica con x la variabile indipendente
– L’insieme in cui può variare la variabile indipendente si chiama
dominio della funzione
– Si indica con y la variabile dipendente
– L’insieme in cui può variare la variabile dipendente si chiama
codominio della funzione
– La funzione si scrive come y=f(x) in cui f rappresenta la legge
di corrispondenza tra gli elementi del dominio e quelli del
codominio
G.M. - Informatica B-Automazione 2002/03
Esempi di funzioni
• La legge di corrispondenza può essere espressa analiticamente
– y(x)=4x2+6x+20
(continua)
• Il dominio coincide con l’insieme dei numeri reali
• il codominio: reali maggiori di 26.5
G.M. - Informatica B-Automazione 2002/03
Esempi di funzioni
– y(x)=sen(x)
(continua)
• Il dominio coincide con l’insieme dei numeri reali
• Il codominio corrisponde all’intervallo
dei numeri reali compreso
tra -1 e 1
G.M. - Informatica B-Automazione 2002/03
Esempi di funzioni
• Oppure può essere espressa a parole
– y(x) = all’intero immediatamente più piccolo di x (non continua)
• Il dominio coincide con l’insieme dei numeri reali
• Il codominio coincide con i numeri relativi (interi con segno)
G.M. - Informatica B-Automazione 2002/03
Esempi di funzioni - l’ottovolante
• Il profilo dell’ottovolante stabilisce la corrispondenza tra la
coordinata orizzontale e quella verticale
G.M. - Informatica B-Automazione 2002/03
Il limite
 1 

limite 
1
n  2  
n
1 2 3 4 5
; ; ; ; ;.....
3 5 7 9 11
•
•
•
•
Data la funzione f(x)
Si definisce il limite di f(x) per x che tende ad xo
Se la funzione è continua e definita in xo è uguale a f(xo)
Altrimenti bisogna guardare il comportamento della
funzione nei pressi di xo
• Esempi.
G.M. - Informatica B-Automazione 2002/03
Calcolo della pendenza
• La pendenza è data da
Dy
 tan 
Dx
Dy
Pendenza 
Dx
Rapporto incrementale
Rapporto incrementale 
Dy


Dx
y(x  Dx)  y(x)

Dx
y(x)
y(x+Dx)
Dx
x

Dy
x+Dx
G.M. - Informatica B-Automazione 2002/03
Pendenza in un punto
• Con un solo punto non posso calcolare il rapporto
incrementale (Dx=0, rapporto incrementale non è definito)
• Per calcolare la pendenza in un punto faccio il limite del
rapporto incrementale per Dx che tende a 0.
y(x  Dx)  y(x)
Dx 0
Dx
Pendenza (x)  lim
• Questo limite si chiama derivata della funzione y(x) in x
• Corrisponde alla pendenza della retta tangente al grafico
nel punto considerato.
G.M. - Informatica B-Automazione 2002/03
La funzione derivata
• La derivata della funzione y(x) in x la indicheremo:
y(x  Dx)  y(x)
Dy dy
 lim

Dx 0
Dx
0
Dx
Dx dx x
derivata di y(x) in x  lim
• Il calcolo del limite del rapporto incrementale può essere
anche inteso come una legge di corrispondenza
– Rappresenta una funzione: la derivata della funzione y(x)
– Calcolando il limite del rapporto incrementale per ogni valore di x
ottengo la funzione derivata:
la funzione derivata della funzione y (x)  y' (x) 
dy
dx
G.M. - Informatica B-Automazione 2002/03
La derivata di una funzione
• Fornisce una misura della variabilità di una funzione reale
di variabile reale all’interno dell’intervallo di definizione.
• Dove la derivata è positiva la funzione è crescente
• Dove la derivata è negativa la funzione è decrescente
• Dove la derivata è nulla la funzione è costante
• Sul grafico della funzione la derivata corrisponde alla
pendenza del grafico: ossia al coefficiente angolare della
retta tangente al grafico nel punto considerato
• Nei punti di massimo o di minimo relativo la pendenza è
nulla: quindi la derivata è nulla.
G.M. - Informatica B-Automazione 2002/03
Calcolo della derivata per via analitica
• Se si conosce l’espressione della funzione x(t)
x = xo + vot + 1/2aot2 con xo= 7.2 m, vo= 11.4 m, ao= -5.0 m
• Si può calcolare il valore della derivata all’istante di tempo t1 (=per es
2s) usando la definizione:
dx
x(t  Dt)  x(t 1)
 lim Dt 0 1

dt t 1
Dt
lim Dt0
lim Dt0
lim Dt0
lim Dt0
x
o

 vo (t1  Dt)  12 a o (t 1  Dt)2  xo  vo (t1 )  12 a o (t1 )2
Dt



x o  vo t1  vo Dt  12 a o (t 1 )2  a ot 1Dt  12 a o (Dt)2  xo  v o (t 1 )  12 a o (t 1)2
x
Dt
2
2
2
1
1
1

v
t

v
Dt

a
(t
)

a
t
Dt

a
(Dt)

x

v
(t
)

a
(t
)
o
o 1
o
2 o 1
o 1
2 o
o
o 1
2 o 1
v Dt  a t Dt 
o
o 1
Dt
1 a (Dt) 2
2 o
 lim
Dt
Dt 0


vo  a o t1  12 a o (Dt) vo  a o t1
G.M. - Informatica B-Automazione 2002/03
Regole per il calcolo della derivata
• Naturalmente, non è neppure necessario fare ogni volta il limite del
rapporto incrementale, ma occorre applicare alcune regole:
df(t) dk
f(t)  k  costante 

0
Funzione costante
dt
dt
F(t)  f(t)  g(t) 
F(t)  f(t)g(t) 
F(t)  kf(t) 
F(t) 
f(t)
g(t)

dF(t) df(t) dg(t)


dt
dt
dt
Somma di funzioni
dF(t) df(t)
dg(t)

g(t)  f(t)
dt
dt
dt
Prodotto
dF(t) dk
df(t)
df(t)

f(t)  k
k
dt
dt
dt
dt
df(t)
dg(t)
g(t)  f(t)
dF(t)
dt
dt

dt
g(t)2
Prodotto di una costante
per una funzione
Rapporto di funzioni
G.M. - Informatica B-Automazione 2002/03
La derivata di alcune funzioni
df(t) dt 
f(t)  t


 mt
m reale
m
m
m1
dt
dt
f()  sen 
df() dsen

 cos
d
d
f()  cos 
df() d cos

 sen
d
d
f(x)  e x

df(x) de x

 ex
dx
dx
f(x)  log (x) 
df(x) dlog(x) 1


dx
dx
x
G.M. - Informatica B-Automazione 2002/03
Derivata di una funzione di funzione
• A volte ci sono funzioni che dipendono da un variabile
attraverso un’altra funzione:
• x(t)=Acos(wt+j)
x=Acos()
con
(t)= wt+j
A,w,jnumeri reali
F(t)  f(g(t)) 
dF(t) df(g(t)) df(g) dg df(g) dg



dt
dt
dt dg
dg dt
dx(t) dAcos(wt  j) d Acos() d d Acos() d




dt
dt
dt
d
d
dt
dx(t) dAcos() d wt  j 

 Asen()w  Awsen(wt  j)
dt
d
dt
G.M. - Informatica B-Automazione 2002/03
Moto rettilineo del punto materiale
• Punto materiale
– Punto geometrico dotato di massa
• Traiettoria
– Il luogo dei punti via via occupati dal punto materiale
• Moto rettilineo
– Moto con traiettoria rettilinea
• Moto di caduta di un grave, moto alternativo dei pistoni nei cilindri,
moto di una automobile lungo una strada diritta, etc.
G.M. - Informatica B-Automazione 2002/03
Descrizione del moto rettilineo
• Studio del moto di caduta di un grave lungo la
verticale
•
Sulla traiettoria definiamo l’asse di riferimento (origine e verso)
•
Usiamo un orologio per trovare la corrispondenza tra l’istante
di tempo e la posizione in cui si trova il punto materiale (t=0s
inizio dell’osservazione)
t (s)
0,00
0,03
0,07
0,10
0,13
0,17
0,20
0,23
0,27
0,30
0,33
0,37
0,40
0,43
x (m)
1,00
0,99
0,98
0,95
0,91
0,86
0,80
0,73
0,65
0,56
0,46
0,34
0,22
0,08
1,20
1,00
x (m)
0,80
0,60
0,40
0,20
0,00
O
G.M. - Informatica B-Automazione 2002/03
Grafico orario
• Asse delle ascisse = variabile
indipendente (il tempo).
– È necessaria una scala, per es.
1cm=0,1s
• Asse delle ordinate = variabile
dipendente (la posizione).
– Anche qui è utile una scala, per es
1 cm=0,2 m
I punti rappresentano le misure, la curva è l’interpolazione.
• La curva interpolante deve essere continua:
• il punto materiale passa per tutte le posizioni intermedie.
• La legge di corrispondenza è una funzione seria,
• ad ogni istante di tempo corrisponde una sola posizione (il corpo non si può trovare
in due luoghi diversi allo stesso istante di tempo).
• Per lo stesso motivo la funzione è continua
G.M. - Informatica B-Automazione 2002/03
Legge oraria
• Il grafico orario può anche essere
rappresentato mlediante una espressione
matematica (legge oraria)
1
x  1,0  9,81t 2
2
x in m
t in s
Uso del grafico orario o della legge
oraria: voglio conoscere la posizione
del punto all’istante 0,2 s.
Con il grafico orario
Con la legge oraria
1
1
x  1,0  9,81 0,2 2  1.0  9,81  0,04  1,0  0,196  0,803 (m)
2
2
G.M. - Informatica B-Automazione 2002/03
Grafico orario di un punto materiale
fermo
• Il grafico orario è una retta parallela all’asse delle ascisse (dei tempi)
(pendenza = 0)
• Legge oraria corrispondente:
x = xo
(x=0,31 m)
G.M. - Informatica B-Automazione 2002/03
Grafico orario di un moto a velocità
costante
La retta:
x=mt+n
n= intercetta asse
ordinate
m= coefficiente
angolare
• Il grafico orario è una retta
Dx
pendenza  tan  
v
Dt
• Legge oraria corrispondente:
x(t)  x o  vt
G.M. - Informatica B-Automazione 2002/03
Moto di un’automobile su un tratto
rettilineo
• Esiste una relazione tra la
pendenza del grafico orario
e la velocità
dell’automobile.
G.M. - Informatica B-Automazione 2002/03
Spostamento e percorso effettuato
• Grafico orario di un corpo lanciato
verso l’alto.
• Legge oraria corrispondente
x = xo + vot + 1/2aot2
• xo= 7.2 m
• vo= 11.4 m
• ao= -5.0 m
xmassimo
xfinale
xiniziale
• Consideriamo gli istanti
– Iniziale: tiniziale
– finale: tfinale
Spostamento= Dx =xfinale-xiniziale
Percorso effettuato: è la lunghezza
del tratto effettivamente percorso
Nel caso della figura d=(xmassimo-x1)+(xmassimo-x2)
G.M. - Informatica B-Automazione 2002/03
Il segno dello spostamento
• Spostamento Dx =xfinale-xiniziale
con Dt > 0
• Nel caso di un moto rettilineo
non è necessario far ricorso alla
rappresentazione vettoriale
– Il verso del moto viene
rappresentato dal segno di Dx
– Se Dx >0 allora vuol dire che
xfinale >xiniziale: il moto è
avvenuto nella direzione
positiva dell’asse delle x
– Se Dx <0 allora vuol dire che
xfinale <xiniziale: il moto è
avvenuto nella direzione
negativa dell’asse delle x
xmassimo
xfinale
xiniziale
G.M. - Informatica B-Automazione 2002/03
Velocità media
• Velocità scalare
percorso effettuato
v sm 
Dt
Grafico Orario
x (m)
25
20
2
x2
– Sempre positiva
15
Dx
Dt
x1 1
• Velocità vettoriale
Dx x2  x1
vm 

Dt
t 2  t1
10
– Positiva -->x crescenti
– Negativa-->x decrescenti
5
0
0
t1 1
2
3 t2
4
t (s) 5
G.M. - Informatica B-Automazione 2002/03
•
Alla guida di un’automobile, dopo aver percorso una strata rettilinea per 8,4
km a 70 km/h, siete rimasti senza benzina. Avete quindi proseguito a piedi,
sempre nella stessa direzione, per 2.0 km fino al prossimo distributore, dove
siete arrivati dopo 30 minuti di cammino. Qual è
–
–
–
Qual è lo spostamento complessivo
Il tempo complessivo impiegato
La velocità media
spost. complessivo 
 8.4km  2.0km  10.4km
tempo totale  Dt 1  Dt 2 
d1
 Dt 2 
v1
8.4km

 0.50h  0.62h
km
70
h

spost. complessivo

tempo totale
10.4km

 16.8 km h
0.62h
vm 
G.M. - Informatica B-Automazione 2002/03