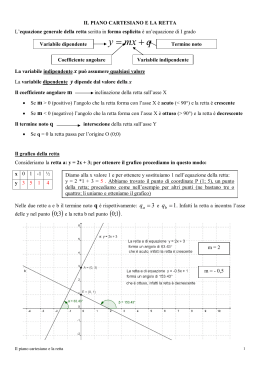
La retta
Prof.ssa Maria Luisa Aira
Obiettivi:
Sapere:
 l’equazione di una retta e rappresentare
sul piano cartesiano.
 Rette parallele agli assi cartesiani
 Parallelismo e perpendicolarità
L’equazione della retta

Rette parallele agli assi:
– Retta parallela all’asse x:
y = k (k = numero qualsiasi)
•
-Retta parallela all’asse y
x = k (k = numero qualsiasi)
Equazioni degli assi:



Come rette orientate anche gli assi
cartesiani hanno un’equazione:
Asse x:
y=0
Asse y:
x=0
Retta passante per l’origine degli
assi
La sua equazione è: y = m  x
m = coefficiente angolare
Se m > 0 la retta forma con il semiasse
positivo delle x un angolo acuto
Se m < 0 la retta forma con il semiasse
positivo delle x un angolo ottuso
Retta in forma generica
La sua equazione è:
y=mx+q
m = coefficiente angolare
q = ordinata all’origine
Grafici:
Rette parallele
Il coeff. angolare di una retta (m) esprime in
termini numerici l’angolo che la retta
forma con la direzione positiva dell’asse
delle ascisse. Poiché due rette parallele
formano gli stessi angoli con il semiasse
positivo delle x, si deduce che:
due rette parallele hanno lo stesso
coeff. angolare
Esempio: y = 3x +1 e y = 3x - 2
Grafico di due rette parallele
Rette perpendicolari
Date due rette generiche di equazione:
y = mx + q e y = m’x+q
la condizione di perpendicolarità è
espressa dalla relazione:
m’ = Es.: y = 3x - 1 e
Grafico di due rette
perpendicolari
Riepilogo
asse x
y=0
asse y
x=0
retta parallela all’asse x
y=k
retta parallela all’asse y
x=k
retta passante per l’origine
y= mx
rette generiche
y= mx + q