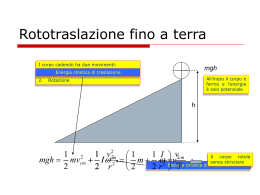
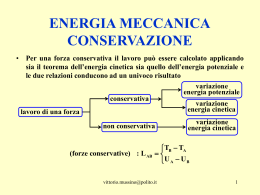
Energia
Energia
Si definisce energia la capacità di compiere un lavoro.
Esistono varie forme di energia.
Energia cinetica: è l’energia
posseduta da un corpo in
movimento.
L  Fs
E per le leggi
del m.r.u.a.
v0  0,
F  cos t.
s
1 2
at
2
1 2
at
per la legge di Newton F=ma
2
1
1
1
1
1
L  ma at 2  ma 2t 2  ma 2t 2  m(at ) 2  mv 2
2
2
2
2
2
LF
Si definisce perciò energia
cinetica, la grandezza
1 2
K  mv
2
s
v  at
F
Se il corpo non parte da fermo
v0  0
Si dimostra (teorema della variazione dell’energia cinetica):
1 2 1 2
L  K  K  K 0 mv  mv0
2
2
Il lavoro compiuto su un corpo è uguale alla variazione
di energia cinetica del corpo stesso
Energia potenziale: è l’energia posseduta da un corpo
posto in un campo gravitazionale.
L  Fs  mgs  mgh
Si definisce perciò
energia potenziale
mg
h
U  mgh
N.B. l’unità S.I. di qualsiasi forma di energia sarà J
Energia meccanica E
Si definisce energia meccanica la somma
dell’energia cinetica e potenziale
E  K U
Per E vale il principio dell’energia meccanica:
In un sistema isolato (su cui quindi non agiscono forze
esterne) l’energia meccanica rimane costante
E  K  U  cost.
K A  U A  KB  U B
Per qualsiasi coppia di
stati A e B
Esempio di applicazione del principio di conservazione
dell’energia meccanica
vA  0
Una sferetta rotola lungo un piano inclinato con
velocità iniziale nulla.
hB  0
A
K A  U A  KB  U B
1 2
1 2
mvA  mgh  mvB  mghB
2
2
h
B
1 2
mgh  mvB
2
v  2 gh
Energia elastica: il caso del lavoro di una forza variabile
Consideriamo il lavoro compiuto
su una molla:
Poiché, per la legge di Hooke:
F  kx
La forza dipende dallo spostamento X,
quindi è variabile.
F
x
F
Grafico della Legge di Hooke
x
Nel caso di una forza variabile, si può
dimostrare che il lavoro, e quindi l’energia, è
dato dall’area sottostante il grafico F,x. Perciò
in questo caso:
bh xF
L  area  
2
2
kx  x
L
2
Energia elastica
2
kx
Eel 
2