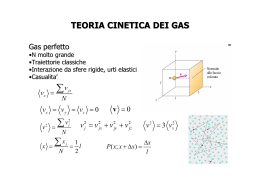
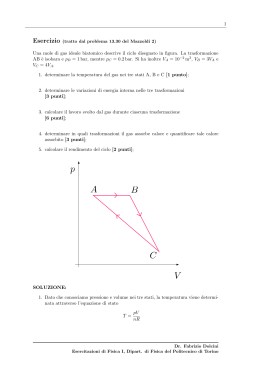
Fisica 1 B, AA 2004-05
II prova in itinere del 24-06-2005, ore 9.00, durata 2 ore
Regole per p.i. e appelli (LEGGERE ATTENTAMENTE PRIMA DI COMINCIARE):
1) la prova è valida se affrontata individualmente; ogni tipo di comunicazione, verificata durante o dopo la prova, comporta
l’invalidazione della stessa. L’avvistamento del telefonino comporta l’immediata espulsione.
2) la prova va affrontata senza alcun ausilio di libri di testo e/o appunti; sul banco devono trovare posto solo testo della prova ed i
fogli forniti (uno solo da consegnare con le soluzioni e lo svolgimento), penna e calcolatrice numerica.
3) i dati necessari alla soluzione sono forniti nel testo della prova.
4) ogni esercizio è accreditato di un punteggio; la sufficienza è 18, mentre il punteggio totale è 36.
5) le p.i. possono sostituire un solo appello estivo; il risultato delle p.i. è automaticamente annullato quando si partecipa ad un
appello regolare estivo.
6) il voto finale viene composto dal risultato delle prove scritte e dalla discussione dell’elaborato che (eventualmente) include
domande di carattere teorico sul corso; la discussione è più approfondita nelle situazioni di limite per assestare la sufficienza o
l’eccellenza, e nei casi di dubbia paternità della prova.
7) nella soluzione dei problemi, sempre fornire prima il procedimento ed il risultato simbolico e successivamente il risultato
numerico; il testo va consegnato su un singolo foglio (quattro facciate) e deve essere scritto in forma leggibile; non verrà considerato
nessun altro foglio incluso, così come le soluzioni che risultano ambigue a causa di disordine o scrittura poco leggibile del candidato.
8) il foglio che si desidera sia considerato al fine della valutazione deve riportare oltre al NOME e COGNOME anche il NUMERO
DI MATRICOLA.
1) Tre moli di gas ideale monoatomico sono contenute in un recipiente di capacità termica
trascurabile. Il sistema è successivamente posto in contatto con una sorgente termica alla
temperatura di 70°C. Raggiunto il nuovo stato di equilibrio si osserva che la variazione di entropia
della sorgente è 500 J/K. Calcolare la variazione di entropia del gas. (7 punti)
2) Un gas ideale biatomico, che si trova inizialmente alla pressione di 5 bar, compie una
trasformazione isoterma che lo porta alla pressione di 2 bar. Successivamente subisce una
trasformazione isocora e quindi una adiabatica tali da riportarlo allo stato iniziale. Disegnare il ciclo
risultante nel piano P-V e valutarne il rendimento. (6 punti)
3) Due moli di gas perfetto, uno monoatomico, l’altro biatomico, inizialmente a pressione P0 = 2
atm e volume V0 sono compresse a metà del volume iniziale adiabaticamente e in modo reversibile.
Calcolare le pressioni finali dei due gas. (5 punti)
4) Un serbatoio di volume V1 = 10 l è riempito con una mole di aria alla temperatura T1 = 283 K.
Mediante una compressione isotermica il volume è portato a V2 = 2 l. Successivamente il gas viene
fatto espandere adiabaticamente fino al volume di 20 l. Le trasformazioni sono tutte reversibili. Si
consideri l’aria un gas perfetto biatomico. Calcolare a) la temperatura finale, b) il lavoro compiuto
dal gas nelle due trasformazioni. (5 punti)
5) Un contenitore metallico (peso atomico = 56, Cv = 25J/mole K, m = 50 kg) si trova inizialmente
alla temperatura T0 = -50 °C. 10 l di acqua a 20°C vengono versati al suo interno. Calcolare a) la
temperatura finale di equilibrio sapendo che il calore latente dell’acqua è 3.33 105 J/kg e b) le
variazioni di entropia del contenitore e dell’acqua. c) Se i coefficienti di dilatazione volumica dei
componenti fossero tutti uguali, valutare se il sistema compie lavoro verso l’esterno. Supporre
trascurabile lo scambio termico con l’aria. (7 punti)
6) Un serbatoio termico alla temperatura T0 = 500 K è posto in contatto con una massa di materiale
di capacità termica C0 = 104 J/K alla temperatura T1= 400 K attraverso una sbarra di rame di
sezione A = 10 cm2, lunghezza L = 50 cm e conducibilità termica K = 400 W/m K. a) Calcolare la
potenza iniziale che fluisce lungo la sbarra. b) Calcolare il calore acquisito dalla massa fino al
raggiungimento dell’equilibrio termodinamico del sistema. c) A partire dai valori ottenuti, stimare il
tempo necessario per raggiungere l’equilibrio. (6 punti)
Soluzioni II prova in itinere Fisica IB 24-06-05
Esercizio 1
TSorgente = 343.15 K
Tigas =
QSorgente
ncV
QSorgente = TSorgente ∆S Sorgente = 171.6 kJ
 TSorgente 
 = −99.6 J / K
∆S gas = ncV ln
 Tigas 


+ TSorgente = 4937 K
Esercizio 2
γ = 1.4
p A = 5atm
p B = 2atm;
QSorgente = −Q gas = −ncV (TSorgente − Tigas )
T A = TB = T
p 
 nRTp A 
V 
 = nRT ln A 
Q AB = L AB = nRT ln B  = nRT ln
 pB 
 nRTp B 
 VA 

 V  γ −1
 nRTp  γ −1 

 p γ −1
5
B 
Q BC = ∆Eint BC = ncV (TC − TB ) = ncV  A  T − T  = ncV T 
− 1 = n RT  B
− 1


 p γ −1

 VC 
 nRTp A 

2

 A




V B = VC
γ −1
QCA = 0
Qh = Q AB
Qc = −Q BC
p 
1 −  B 
Q
5
 pA 
η = 1− c = 1−
Qh
2
p 
ln A 
 pB 
p
A
B
= 0.16
C
V
Esercizio 3
pi = 2atm; V f =
Vi
;
2
piVi γ = p f V fγ = p f
gas monoatomico γ = 1.67
1
2γ
Viγ
p f = 2 γ pi
p f = 2 γ pi = 6.36 atm; gas biatomico γ = 1.40
p f = 2 γ pi = 5.28 atm
Esercizio 4
V1 = 10 l ;
V2 = 2 l ;
V 
T1 = 283K ; T2V2γ −1 = T3V3γ −1 T3 = T2  2 
 V3 
V3 = 20l ;
γ −1
V 
= T1  2 
 V3 
γ −1
= 113K
V 
5
5
Liso = nRT1 ln 2  = −3.78kJ ; Ladiab = − ∆Eint 23 = − n R(T3 − T2 ) = −n R (T3 − T1 ) = 3.5kJ
2
2
 V1 
Esercizio 5
T1 = 223.15K; Ta = 293.15K; Tfase = 273.15K; m = 50Kg; m a = 10Kg; c v = 25J/(moleK); Pm = 56g/mole;
c a = 4186J/(Kg K); L = 3.33 ⋅ 10 5 J/Kg;
(
)
Q a = Q a1 + Q a2 = ma c a T fase − Ta − ma L = −0.87 MJ − 3.3MJ = −4.17 MJ
Qm =
(
)
m
cV T fase − T0 = 1.12 MJ
Pm
Qm > Q a1 quindi l' acqua arriva alla temperatura di transizione di fase, ma siccome Qm < Q a non si trasforma
tutta in ghiaccio. La temperatura di equilibrio è Tfase .
Detta x la frazione di acqua che si trasforma in ghiaccio e xm a la massa di ghiaccio formata si ha
(
ma c a T fase
∆S m =
∆STOT
(
)
)
m
cV T fase − T0 = 0
− Ta − xma L +
Pm
 T fase 
m
 = 4.5kJ / K
cV ln

Pm
 T0 
= ∆S m + ∆S a = 0.52kJ / K
(
)
∆Vm = 3α Vm T fase − T1 = 3α Vm ∆Tm
(
)
x=
 T fase
∆S a = ma ca ln
 Ta
(
)
 xma L
−
= −3.98kJ / K
 T
fase

)
∆Va = 3α Va T fase − Ta = −3α Va ∆Ta
⇒ il sistema compie lavoro verso l' esterno se ∆V > 0 cioè
(
m
cV T fase − T0
Pm
= 0.0837
ma L
ma c a T fase − Ta +
∆V = 3α(Vm ∆Tm − Va ∆Ta )
V m > V a ∆ Ta ∆ Tm
Esercizio 6
T0 = 500 K ; T1 = 400 K ; c0 = 104 J / K ; A = 10 cm 2 ; L = 50 cm; K = 400 W /( Km);
dQ A
Q
= K (T0 − T1 ) = 80W
Q = c0 (T0 − T1 ) = 10.4kJ
t > t min =
= 130s
dt
L
(dQ dt )max