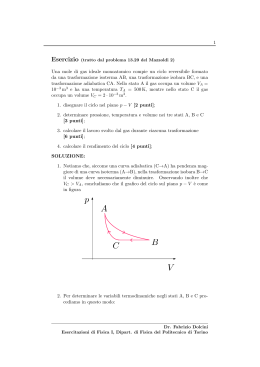
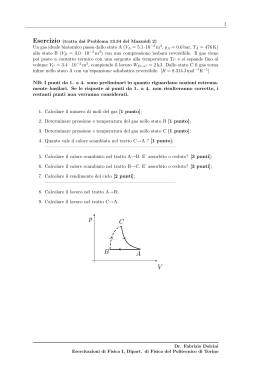
1
Esercizio
(tratto dal problema 13.30 del Mazzoldi 2)
Una mole di gas ideale biatomico descrive il ciclo disegnato in figura. La trasformazione
AB è isobara e pB = 1 bar, mentre pC = 0.2 bar. Si ha inoltre VA = 10−2 m3 , VB = 3VA e
VC = 4VA .
1. determinare la temperatura del gas nei tre stati A, B e C [1 punto];
2. determinare le variazioni di energia interna nelle tre trasformazioni
[3 punti];
3. calcolare il lavoro svolto dal gas durante ciascuna trasformazione
[6 punti];
4. determinare in quali trasformazioni il gas assorbe calore e quantificare tale calore
assorbito [3 punti];
5. calcolare il rendimento del ciclo [2 punti];
p
A
B
C
V
SOLUZIONE:
1. Dato che conosciamo pressione e volume nei tre stati, la temperatura viene determinata attraverso l’equazione di stato
T =
pV
nR
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
2
e dunque abbiamo
pB VA
pA VA
=
=
nR
nR
1 · 105 mN2 10−2 m3
TA =
=
1 mol · 8.314 molJ K
= 120 K
TB =
=
=
pB VB
=
nR
1 · 105 mN2 3 · 10−2 m3
1 mol · 8.314 molJ K
= 361 K
TC
=
=
pC VC
=
nR
0.2 · 105 mN2 4 · 10−2 m3
1 mol · 8.314 molJ K
= 96.2 K
(1)
=
(2)
=
(3)
2. Nel gas perfetto l’energia interna dipende solo dalla temperatura (U = ncV T ); ricordando che per un gas biatomico
5
cV = R
2
(gas biatomico)
(4)
abbiamo
• ∆UAB = U (B) − U (A) = ncV (TB − TA ) =
pB VB − pA VA
= ncV
=
nR
cV
=
(pB VB − pA VA ) =
R
5
=
(pB VB − pA VA ) =
2
5
=
pB (VB − VA )
2
N
= 2.5 · 1 · 105 2 3 · 10−2 m3 − 10−2 m3 =
m
= 5.0 · 103 J
• ∆UBC
= U (C) − U (B) = ncV (TC − TB ) =
pC VC − pB VB
=
= ncV
nR
cV
=
(pC VC − pB VB ) =
R
5
=
(pC VC − pB VB ) =
2
N
N
= 2.5 · 1 0.2 · 105 2 4 · 10−2 m3 − 105 2 · 3 · 10−2 m3 =
m
m
= −5.5 · 103 J
(5)
(6)
(7)
(8)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
3
• ∆UCA = U (A) − U (C) = ncV (TA − TC ) =
pA VA − pC VC
= ncV
=
nR
cV
=
(pA VA − pC VC ) =
R
5
(pA VA − pC VC ) =
(9)
=
2
N
N
= 2.5 · 1 1 · 105 2 · 10−2 m3 − 0.2 · 105 2 · 4 · 10−2 m3 =
m
m
= 0.5 · 103 J
(10)
3. Per calcolare il lavoro, ricordiamo che il significato geometrico di
Z
W = p dV
è quello dell’area (con segno) sottesa dalla curva della trasformazione (vedi Fig.1).
Pertanto abbiamo
p
pB
p
p
A
B
pB
B
pC
VA
VB
VC
A
pC
C
VB
V
pA
V
C
VA
VC
V
Figure 1:
• Trasformazione A→B. Si tratta dell’area (con segno positivo) del rettangolo
WAB = pB (VB − VA ) =
N
= 105 2 (3 − 1) · 10−2 m3 =
m
= 2.0 · 103 J
(lavoro eseguito)
(11)
• Trasformazione B→C. Si tratta dell’area (con segno positivo) del trapezio
WBC
pB + pC
(VC − VB ) =
2
(1.0 + 0.2) · 105 mN2
=
(4 − 3) · 10−2 m3 =
2
= 0.6 · 103 J
(lavoro eseguito)
=
(12)
• Trasformazione C→A. Si tratta dell’area (con segno negativo) del trapezio
pA + pC
(VC − VA ) =
2
(1.0 + 0.2) · 105 mN2
= −
(4 − 1) · 10−2 m3 =
2
= −1.8 · 103 J
(lavoro subı̀to)
WCA = −
(13)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
4
4. Per calcolare il calore in ciascuna trasformazione possiamo utilizzare il primo principio
Q = ∆U + W
(14)
• Trasformazione A→B.
QAB = ∆UAB + WAB = 5.0 · 103 J + 2.0 · 103 J =
= 7.0 · 103 J
(calore assorbito)
(15)
• Trasformazione B→C.
QBC
= ∆UBC + WBC = −5.5 · 103 J + 0.6 · 103 J =
= −4.9 · 103 J
(calore ceduto)
(16)
• Trasformazione C→A.
QCA = ∆UCA + WCA = 0.5 · 103 J − 1.8 · 103 J =
= −1.3 · 103 J
(calore ceduto)
(17)
W
=
Qass
WAB + WBC + WCA
=
=
QAB
(2.0 + 0.6 − 1.8) · 103 J
=
=
7.0 · 103 J
= 0.11
(18)
• Il rendimento del ciclo è dato da
η =
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino