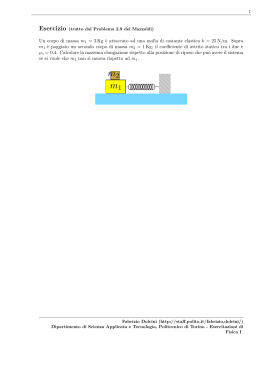
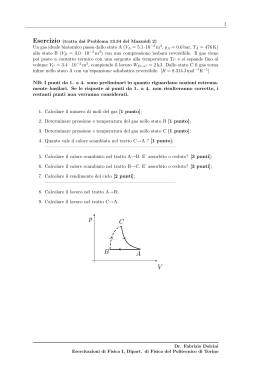
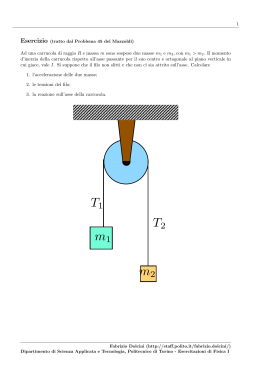
1
Esercizio
(tratto dal Problema 3.27 del Mazzoldi 2)
Un corpo di massa mA = 2 Kg è posto su un piano orizzontale liscio. Esso è collegato tramite due
fili a due corpi di masse mB = 4 Kg e mC = 1 Kg. Calcolare:
1. l’accelerazione del sistema delle tre masse
2. le tensioni dei due fili
mA
mB
mC
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di
Fisica I
2
SOLUZIONE
Dati Iniziali
mA = 2 Kg
mB = 4 Kg
mC = 1 Kg
• Disegniamo anzitutto le forze che agiscono su ciascun corpo. Si tratta di forza peso e tensione
dei fili, come mostrato in figura.
T1
mA
T2
T1
T2
mB
mC
mB g
mC g
• Osserviamo che, siccome i fili sono supposti inestensibili, l’accelerazione è la stessa in modulo
per tutte le parti del sistema. Indichiamo con a tale accelerazione e scegliamo un verso
convenzionale, che è arbitrario ma deve essere consistente per tutte le parti del sistema.
a
mA
mB
a
mC
a
• Scriviamo par per ciascun corpo del sistema la seconda legge della dinamica
F = ma
tenendo conto del verso convenzionale scelto. Abbiamo

= mB g − T1 (I)
 mB a
−mA a = T2 − T1
(II)

−mC a = mC g − T2 (III)
(1)
(2)
Abbiamo dunque un sistema di tre equazione in tre incognite T1 , T2 e a.
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di
Fisica I
3
• Risolviamo il sistema. Dalla combinazione (I) − (II) − (III) otteniamo
(mB + mA + mC )a = mB g − T1 − (T2 − T1 ) − (mC g − T2 ) =
= mB g − mC g
(3)
da cui
a=
(mB − mC ) g
mA + mB + mC
(4)
Sostituendo ora i valori numerici otteniamo
(4 Kg − 1 Kg) 9.81 m/s2
=
(2 + 4 + 1) Kg
3
m
=
· 9.81 2 =
7
s
m
= 4.2 2
s
a =
(5)
• Sostituiamo ora il risultato (4) nell’Eq.(I) del sistema (2), ed otteniamo
mB a = mB g − T1
⇓
T1 = mB g − mB a = mB (g − a) =
(mB − mC )g
=
= mB g −
mA + mB + mC
mB − mC
= mB g 1 −
=
mA + mB + mC
mA + 2mC
= mB
g
mA + mB + mC
(6)
Sostituendo i valori numerici otteniamo
T1 = mB
mA + 2mC
mA + mB + mC
g
(7)
mentre per T1 otteniamo
T1 =
=
=
=
=
mA + 2mC
mB
g=
mA + mB + mC
(2 Kg + 2 · 1Kg)
m
4 Kg
· 9.81 2 =
(2 + 4 + 1) Kg
s
4
m
4 Kg · · 9.81 2 =
7
s
m
22.4 Kg 2 =
s
22.4 N
(8)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di
Fisica I
4
• Sostituiamo infine (4) e (7) nella (III) del sistema (2)
− mC a = mC g − T2
⇓
T2 = mC g + mC a = mC (g + a) =
(mB − mC )g
= mC g +
=
mA + mB + mC
mB − mC
=
= mC g 1 +
mA + mB + mC
mA + 2mB
= mC
g
mA + mB + mC
(9)
ossia
T2 = mC
mA + 2mB
mA + mB + mC
g
(10)
Sostituendo i valori numerici otteniamo
T2 = mC
=
=
=
=
mA + 2mB
g=
mA + mB + mC
2 Kg + 2 · 4Kg
m
1 Kg
· 9.81 2 =
(2 + 4 + 1) Kg
s
10
m
· 9.81 2 =
7
s
m
14.0 Kg 2 =
s
14.0 N
(11)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di
Fisica I