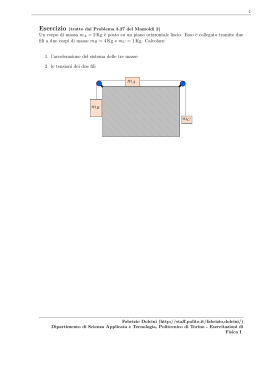
1
Esercizio
(tratto dal Problema 45 del Mazzoldi)
Ad una carrucola di raggio R e massa m sono sospese due masse m1 e m2 , con m1 > m2 . Il momento
d’inerzia della carrucola rispetto all’asse passante per il suo centro e ortogonale al piano verticale in
cui giace, vale I. Si suppone che il filo non slitti e che non ci sia attrito sull’asse. Calcolare
1. l’accelerazione delle due masse;
2. le tensioni del filo;
3. la reazione sull’asse della carrucola.
T1
T2
m1
m2
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
2
SOLUZIONE
Scegliamo anzitutto un verso convenzionale per il moto. Siccome il problema dice che la massa m1
è più grande, sembra naturale (anche se non è obbligatorio) scegliere il verso mostrato in figura 1
Scriviamo ora
N
T1
T2
mg
T1
m1
T2
m2
m2 g
m1 g
Figure 1:
• equazione per il corpo m1
m1 g − T1 = m1 a
(1)
− m2 g + T2 = m2 a
(2)
• equazione per il corpo m2
• equazione per la carrucola. La carrucola è un corpo rigido. Pertanto in generale abbiamo due
equazioni, una per il moto traslatorio del centro di massa, e l’altro per il moto rotatorio attorno
al centro di massa.
– Le forze che agiscono sulla carrucola sono
∗ la tensione T1 e T2 dei fili applicati alla carrucola (si noti che ciascuna parte di filo,
a destra e a sinistra della carrucola, ha massa nulla, e dunque le tensioni ai capi di
ciascuna parte di filo sono uguali ed opposte);
∗ la forza peso dovuta alla massa del disco della carrucola;
∗ la reazione vincolare N del perno della carrucola.
In questo caso il centro di massa è fermo, dato che la reazione vincolare N del perno non
lo fa muovere
− T1 − T2 − mg + N = 0
(3)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
3
– Per scrivere l’equazione per i momenti dobbiamo anzitutto scegliere un polo. Scegliamo
come polo il centro del disco. Dato che la carrucola ruota sul piano del foglio, l’asse
di rotazione ha come direzione quella perpendicolare al foglio; scegliamo come versore k̂
quello nel verso uscente. Allora l’unica componente delle equazioni dei momenti è quella
lungo k̂, e vale
Iα = M
(4)
dove α è l’accelerazione angolare (positiva per accelerazione in senso antitorario, dato che
k̂ è nel verso uscente), e M è la componente lungo k̂ del momento delle forze applicate.
– Mentre la forza peso mg e la reazione vincolare N del perno danno momento nullo (perché
sono applicate proprio al polo), la tensione T1 applicata al disco dà un momento diretto
lungo k̂, mentre la tensione T2 applicata al disco dà un momento diretto nel verso entrante
(opposto a k̂). Quindi il momento totale è
M = (T1 − T2 ) R
(5)
Iα = (T1 − T2 ) R
(6)
Inserendo (5) in (4) otteniamo
– Utilizziamo ora il fatto che il filo non slitta. Dunque la carrucola ruota senza strisciare
contro il filo, e allora l’accelerazione angolare α e l’accelerazione longitudinale a dei corpi
connessi al filo sono legati da
a
α=
(7)
R
Sostituendo (7) in (6) otteniamo
I
a 2 = T1 − T2
(8)
R
Quindi le tre equazioni (1), (2) e (8)

m1 g − T1 = m1 a






−m2 g + T2 = m2 a





I
 T −T
= a 2
1
2
R
(9)
costituiscono un sistema di tre equazioni in tre incognite a, T1 e T2 . Sommando le tre equazioni si
ottiene
I
(10)
(m1 − m2 )g = (m1 + m2 + 2 ) a
R
da cui
m1 − m2
(11)
a=g
m1 + m2 + RI2
Dalla prima equazione di (9) ricaviamo ora che
T1 = m1 (g − a) =
m1 − m2
= m1 g 1 −
m1 + m2 + RI2
= m1 g
2m2 +
I
R2
m1 + m2 +
I
R2
!
=
(12)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
4
e dunque
T1 = m1 g
2m2 +
I
R2
m1 + m2 +
(13)
I
R2
Dalla seconda equazione di (9) ricaviamo ora che
T2 = m2 (g + a) =
m1 − m2
= m2 g 1 +
m1 + m2 + RI2
= m2 g
2m2 +
!
=
I
R2
m1 + m2 +
(14)
I
R2
e dunque
T2 = m2 g
2m1 +
I
R2
m1 + m2 +
(15)
I
R2
La reazione vincolare si calcola allora dalla (3)
N
= T1 + T2 + mg =
2m1 + RI2
2m2 + RI2
+
m
g
+ mg =
= m1 g
2
m1 + m2 + RI2
m1 + m2 + RI2
= g
= g
4m1 m2 +
I
)
R2
I
) + m(m1 + m2
R2
m1 + m2 + RI2
m(m1 + m2 ) + RI2 (m + m1 + m2 )
m1 + m2 + RI2
m1 (2m2 +
+ m2 (2m1 +
+
I
)
R2
=
(16)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I