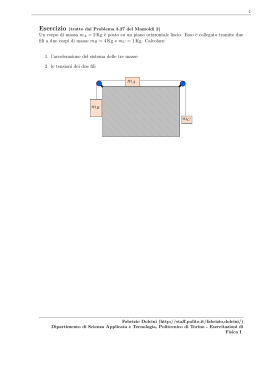
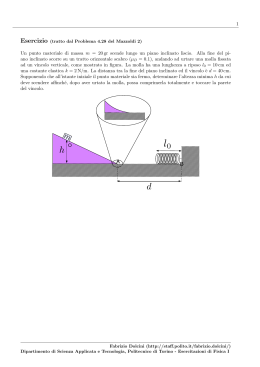
1
Esercizio
(tratto dal Problema 4.29 del Mazzoldi 2)
Un corpo di massa m = 1.5 Kg è agganciato ad una molla di costante elastica k = 2 N/m, di lunghezza
a riposo l0 = 50 cm, fissata ad una parete verticale in x = 0. Il piano su cui si trova il corpo è liscio.
All’istante t = 0 al corpo viene impressa una velocità iniziale v0 = 0.2 m/s verso destra.
1. scrivere la legge oraria x(t) del corpo;
2. calcolare l’energia cinetica del corpo e tracciare il suo andamento nel tempo;
3. calcolare l’energia potenziale del corpo e tracciare il suo andamento nel tempo;
4. mostrare che l’energia meccanica si conserva;
5. utilizzando la conservazione dell’energia calcolare l’allungamento massimo ∆xmax > 0 della
molla verso destra.
6. utilizzando la conservazione dell’energia calcolare la velocità del corpo quando comprime la molla
verso sinistra di una quantità ∆xB = −∆max /2.
l0
m
x=0
v0
x
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
2
SOLUZIONE
DATI INIZIALI
m = 1.5 Kg
(1)
k = 2 N/m
(2)
l0 = 0.5 m
(3)
v0 = 0.2 m/s
(4)
• posizione iniziale
x(t = 0) = l0
(5)
v(t = 0) = v0
(6)
• velocità iniziale
1. La legge oraria si ricava risolvendo le equazioni della dinamica.
∆x
l0
m
x
Il corpo è soggetto alla sola forza elastica della molla. Indicando con x la coordinata del corpo
m lungo il piano (misurata rispetto all’origine posta alla parete verticale) abbiamo
Fel (x) = −k(x − l0 )
(7)
dove l0 è la lunghezza a riposo della molla. Quindi abbiamo
ma = Fel
⇓
m
d2 x
dt2
= −k(x − l0 )
⇓
d2 x
dt2
= −
k
(x − l0 )
m
(8)
Questa è l’equazione differenziale che dobbiamo risolvere, con le condizioni iniziali (relative
all’istante in cui il punto materiale parte da O verso destra)

 x(t = 0) = l0
(9)

v(t = 0) = v0
Per risolvere l’Eq.(8) osserviamo che è simile all’equazione di un moto armonico
d2 y
= −ω 2 y
dt2
(10)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
3
di cui è nota la soluzione generale
y(t) = A cos(ωt) + B sin(ωt)
(11)
dove A e B sono due costanti arbitrarie (il cui valore deve determinarsi imponendo le condizioni
iniziali). Tentiamo pertanto di riscrivere la (8) nella forma di un’equazione armonica (10)
A tale scopo osserviamo che, siccome l0 è costante, possiamo scrivere (8) anche come
d2 (x − l0 )
dt2
= −
Pertanto, definendo
ω2 =
k
(x − l0 )
m
(12)
k
m
(13)
e introducendo la variabile
∆x(t) = x(t) − l0
(14)
(che rappresenta lo scostamento rispetto alla lunghezza a riposo della molla) otteniamo che la
variabile ∆x soddisfa l’equazione differenziale
d2 (∆x)
dt2
= −ω 2 ∆x(t)
(15)
La (15) è proprio l’equazione del moto armonico (10). La soluzione generale (11) vale dunque
∆x(t) = A cos(ωt) + B sin(ωt)
(16)
Ricordando la relazione (14) tra x e ∆x, otteniamo la soluzione generale dell’Eq.(8)
r
k
x(t) = l0 + A cos(ωt) + B sin(ωt)
ω=
m
(17)
e la velocità è
r
dx
v(t) =
= −Aω sin(ωt) + Bω cos(ωt)
dt
ω=
k
m
Le costanti A e B si determinano imponendo le condizioni iniziali (9)

 x(t = 0) = l0 + A cos(ω 0s) + B sin(ω 0s) = l0

da cui
(18)
(19)
v(t = 0) = −Aω sin(ω 0s) + Bω cos(ω 0s) = v0

 A

= 0
Bω = v0
(20)
⇒B=
v0
ω
Sostituendo i valori di A e B ottenuti nella soluzione generale (18) otteniamo
r
v0
k
x(t) = l0 +
sin(ωt)
ω=
ω
m
(21)
e la velocità è
v(t) =
dx
= v0 cos(ωt)
dt
(22)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
4
2. Calcoliamo l’energia cinetica
1
mv 2 =
2
[uso (22)]
1
=
mv 2 cos2 (ωt)
2 0
K =
(23)
ossia
1
K(t) = mv02 cos2 (ωt)
2
(24)
che ha un andamento oscillatorio.
3. Calcoliamo l’energia potenziale. L’energia potenziale elastica è
1
k(x(t) − l0 )2 =
2
[uso (21)]
1 v02
=
k
sin2 (ωt) =
2 ω2
[uso (13)]
1
=
mv 2 sin2 (ωt)
2 0
Ep =
(25)
Anche Ep ha un andamento oscillatorio, sfasato rispetto a quello dell’energia cinetica K.
1
Ep (t) = mv02 sin2 (ωt)
2
(26)
4. Calcoliamo ora l’energia meccanica
Em = K(t) + Ep (t) =
1
1
mv02 cos2 (ωt) + mv02 sin2 (ωt) =
=
2
2
1
2
=
mv
2 0
(27)
Dunque, mentre l’energia cinetica e l’energia potenziale dipendono dal tempo, l’energia meccanica è indipendente dal tempo, ossia si conserva, come mostrato in Fig.1
Em si conserva
(28)
m
Em è costante nel tempo
(29)
m
∆Em = 0
(la variazione di Em è nulla)
(30)
5. Denotiamo ora con tA l’istante in cui il punto materiale raggiunge il punto A di massimo allungamento della molla a destra e indichiamo con ∆xmax tale allungamento massimo. Allora
per definizione
∆x(tA ) = ∆xmax
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
5
Em
Ep
K
π
ω
t
Figure 1: Andamento nel tempo dell’energia cinetica K, energia potenziale elastica Ep , e dell’energia meccanica.
Mentre K e Ep variano nel tempo [vedi Eq.(24) e (26)], la loro somma Em rimane costante, e pari all’energia
iniziale (in questo caso 21 mv02 ).
In corrispondenza dell’allungamento massimo il corpo m si trova alla coordinata x(tA ) = l0 +
∆xmax .
Dato che l’energia meccanica si conserva possiamo scrivere che
Em (t = 0) = Em (tA )
⇓
K(t = 0) + Ep (t = 0) = K(tA ) + Ep (tA )
(31)
Osserviamo ora che
• all’istante t = 0 l’energia cinetica vale
1
K(t = 0) = mv02
2
(32)
• all’istante t = 0 l’energia potenziale elastica è nulla perché il corpo si trova esattamente
alla lunghezza di riposo della molla (la molla non è allungata né compressa)
1
Ep (t = 0) = k (x(t = 0) − l0 )2 = 0 J
2
(33)
• all’istante t = tA di massimo allungamento l’energia cinetica si annulla, dato che il punto
di massimo allungamento è caratterizzato proprio dal fatto che la velocitè a si annulla (la
direzione del moto si inverte)
Ep (tA ) = 0 J
(34)
• all’istante t = tA di massimo allungamento l’energia potenziale elastica vale
1
Ep (tA ) = k (∆xmax )2
2
(35)
Sostituendo (32), (33), (34) e (35) in (31) otteniamo
1
mv 2 =
2 0
1
k (∆xmax )2
2
(36)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
6
da cui otteniamo che l’allungamento massimo è determinato da
m
(∆xmax )2 = v02
k
(37)
Dato che si tratta di un allungamento, ∆xmax è positivo (∆xmax > 0); se fosse una compressione
sarebbe ∆xmax < 0. Pertanto scegliamo la radice positiva. Ricordando inoltre (13) otteniamo
r
m
∆xmax =
v0
(38)
k
Sostituendo i valori numerici si ottiene
l0
∆xmax
xB
m
l0
∆xB
m
l0 B
A
r
m
v0 =
k
s
1.5 Kg
m
0.2
N
s
2m
∆xmax =
=
uso N = Kg m/s2
s
0.75 Kg
m
=
0.2 =
Kg
s
s2
√
m
=
0.75 s2 0.2 =
s
= 0.17 m
(39)
La coordinata del punto di massimo allungamento vale dunque
xA = l0 + ∆xmax =
r
m
= l0 +
v0 =
k
= 0.50 m + 0.17 m =
= 0.67 m
(40)
6. Denotiamo ora con tB l’istante in cui il punto materiale raggiunge il punto B (a sinistra della posizione della lunghezza a riposo) che corrisponde ad una variazione ∆xB = −∆xmax /2 (negativa
= compressione). Dato che l’energia meccanica si conserva possiamo scrivere che
Em (t = 0) = Em (tB )
⇓
K(t = 0) + Ep (t = 0) = K(tB ) + Ep (tB )
(41)
I valori di K(t = 0) e Ep (t = 0) sono stati determinati in (32) e (33), mentre
• all’istante t = 0 l’energia cinetica vale
1
2
K(tB ) = mvB
2
(42)
dove vB è la velocità al punto B (da daterminarsi)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
7
• all’istante t = tB l’energia potenziale elastica vale
1
k (∆xB )2 =
2
∆xmax 2
1
k −
=
=
2
2
[uso ora la (38)]
1 m 2
k
v =
=
2 4k 0
1
=
m v02
8
Ep (tB ) =
(43)
Sostituendo (32), (33), (42) e (43) in (41) otteniamo
1
mv 2 =
2 0
Semplificando per m/2 otteniamo
1
1
2
mvB
+ m v02
2
8
3
2
vB
= v02
4
In conclusione
(44)
(45)
√
3
v0
(46)
2
dove il segno ‘-’ si riferisce a quando il corpo viaggia verso sinistra, ed il segno ‘+’ a quando
il corpo sta ritornando verso la posizione di riposo della molla.
vB = ±
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I