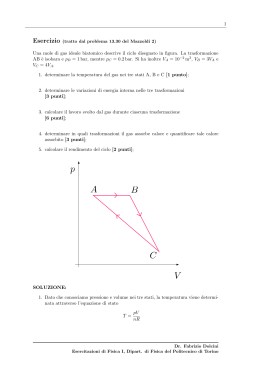
IX ESERCITAZIONE - 16 Dicembre 2013
I.
RENDIMENTO
Un gas perfetto monoatomico compie il ciclo schematicamente mostrato in figura, attraverso
trasformazioni reversibili. I valori di pressione e volume sono i seguenti: PA = 2 · 105 Pa,
VA = 2`, PB = 5PA , VC = 3VA . Calcolare il rendimento η del ciclo.
Soluzione
d
Il rendimento è η = L/Qass . Il lavoro compiuto nel ciclo è pari all’area del triangolo ABC:
1 ¯ ¯
L = AC
BC = 4VA PA = 1600 J
2
(1)
¯ e si ottiene dal primo principio:
Il calore viene assorbito nel tratto AB
Qass = QAB = LAB + ∆UAB = AreaABVA VC + ncV (TB − TC )
(2)
¯ A = 2400 J
Area = L + VA¯VC AV
PB VB PA VA
∆UAB = ncV
−
= 21PA VA = 8400 J
nR
nR
(3)
dove
da cui Qass = 10800J e η = 15%
(4)
2
II.
MACCHINA DI CARNOT
Una macchina di Carnot assorbe una certa quantità di calore Q1 da una sorgente a temperatura T1 e cede calore Q2 ad una seconda sorgente a temperatura T2 = 40%T1 . Determinare
il rendimento η della macchina, il lavoro compiuto durante il ciclo e il calore ceduto.
Soluzione
Il rendimento di una macchina di Carnot in funzione delle temperature è:
η =1 −
T2
= 1 − 0.4 = 60%
T1
Il lavoro compiuto nel ciclo è L = ηQ1 ; il calore assorbito è |Q2 | = |Q1 |(1 − η).
(5)
3
III.
LAVORO
Un gas perfetto biatomico è contenuto in un cilindro chiuso da un pistone. Inizialmente,
si trova nello stato caratterizzato da TA = 300K, VA = 4`, PA = 1atm. Il gas viene poi
compresso adiabaticamente fino a VB = 1`, poi raffreddato a V = cost finché la temperatura
non raggiunge il valore iniziale TA . Il gas viene infine lasciato espandere isotermicamente
fino al volume iniziale VA . Disegnare il ciclo nel piano PV e calcolare il lavoro totale.
Soluzione
L = LAB + LBC + LCA = −∆UAB + LCA = ncV (TA − TB ) + nRTA ln
VA
VC
(6)
Dobbiamo ricavare TB = (PB VB )/(nR):
nR =
PA VA
= 1.35 JK −1
TA
7
(7)
PA VAγ = PB VBγ → PB = 4 5 PA
(8)
PA VB
= 522.96 K
nR
(9)
7
TB = 4 5
da cui
5
L = nR(TA − TB ) + nRTA ln 4 = −189.79 J
2
(10)
4
IV.
ISOCORA IRREVERSIBILE
Una mole di gas perfetto monoatomico compie un ciclo tra gli stati ABCA, secondo le
seguenti trasformazioni: • A→B isoterma reversibile; • B→C isobara reversibile; • C→A
isocora irreversibile, durante la quale il sistema viene riportato nello stato A mediante il solo
scambio di calore QCA (LCA = 0J).
Disegnare il ciclo nel piano PV; calcolare il calore scambiato in ciascuna trasformazione e il
calore totale (in modulo e segno); calcolare il lavoro compiuto in ciascuna trasformazione e
il lavoro totale (in modulo e segno). Dati: VA = 5`, VB = 10`, PA = 1atm, PB = 0.5atm.
Soluzione
VB
= nRTA ln 2
VA
(11)
QBC = ncP (TC − TB ) = ncP (TC − TA )
(12)
QCA = ncV (TA − TC )
(13)
QAB = LAB = nRTA ln
Dobbiamo ricavare TA e TC . La prima si ottiene dall’equazione dei gas perfetti applicata
allo stato A, la seconda imponendo che P/(nR) = cost nel tratto BC:
PA V A
= 60.85 K
nR
TB TC
TA
=
→ TC =
VB VC
2
TA =
da cui QAB = 351.08J, QBC = −633.12J, QCA = 379.87J, Qtot = 97.83J.
(14)
(15)
5
LAB = QAB = 351.08 J
(16)
LBC = PB (VC − VB ) = −PB VA = −253.25 J
(17)
LCA = 0 J
(18)
Ltot = 97.83 J
(19)
Nota bene: Qtot = Ltot , poiché in un ciclo ∆Utot = 0J.
6
V.
CICLO REVERSIBILE
Una mole di gas perfetto monoatomico compie il seguente ciclo: • A→B isoterma reversibile
a TA = 400K che porta a VB = 2VA ; • B→C isocora reversibile; • C→A compressione
adiabatica reversibile.
Disegnare il ciclo nel piano PV; calcolare il calore totale scambiato e il rendimento η del
ciclo.
Soluzione
Qtot = QAB + QBC = LAB + QBC =
= nRTA ln
(20)
VB
+ ncV (TC − TB ) = nRTA ln 2 + ncV (TC − TA )
VA
(21)
Dobbiamo ricavare TC : utilizziamo la relazione tra T e V in un’adiabatica (tratto CA):
TC VCγ−1 = TA VAγ−1 → TC =
1 2/3
TA = 251.98 K
2
(22)
tenuto conto che VB = 2VA . Il calore totale scambiato è Qtot = 459.00J. Il rendimento del
ciclo:
η=
L
Qtot
=
= 20%
Qass QAB
(23)
7
VI.
TRASFORMAZIONI REVERSIBILI
Una mole di gas perfetto monoatomico è nello stato A (TA = 300K, VA = 1`). Il gas compie le
seguenti trasformazioni reversibili: • A→B isoterma fino a VB = 3VA ; • B→C isocora fino a
TC = 144.2K; • C→D compressione adiabatica fino a VD = VA . Disegnare il ciclo nel piano PV.
Determinare P(atm), V(`), T(K) in ognuno dei 4 stati. Determinare il calore scambiato in
ogni trasformazione, in modulo e segno. Calcolare il lavoro compiuto in ogni trasformazione,
in modulo e segno. Calcolare la variazione di energia interna in ogni trasformazione, in
modulo e segno. Se D ≡ A, calcolare il rendimento η del ciclo.
Soluzione
Stato A:
TA = 300 K; VA = 1`; PA =
nRTA
= 2.49 · 106 P a
VA
(24)
Stato B:
TB = TA = 300 K; VB = 3VA = 3`; PB =
nRTB PA
=
= 8.31 · 105 P a
VB
3
(25)
Stato C:
TB = 144.2 K; VC = 3VA = 3`; PC =
nRTC
= 3.99 · 105 P a
VC
(26)
Stato D:
ovvero D ≡ A.
VD = VA = 1`
(27)
TD VAγ−1 = TC (3VA )γ−1 → TD = 32/3 TC = 300 K = TA
(28)
P D = PA
(29)
8
Calori scambiati:
QAB = LAB = nRTA ln
VB
= 2738.84 J
VA
(30)
QBC = ncV (TC − TB ) = ncV (TC − TA ) = −1942.05 J
(31)
QCA = 0 J
(32)
LAB = QAB = 2738.84 J
(33)
LBC = 0 J
(34)
LCA = −∆UCA = ncV (TC − TA ) = QBC = −1942.05 J
(35)
Lavori compiuti:
Variazioni di energia interna:
∆UAB = 0 J
(36)
∆UBC = QBC = −1942.05 J
(37)
∆UCA = −QBC = −1942.05 J
(38)
Nota bene: ∆Utot = 0J (ciclo).
Il rendimento del ciclo è:
η=
L
Qtot
|QBC |
=
=1 −
= 29%
Qass QAB
|QAB |
(39)