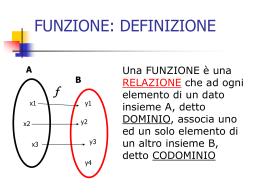
FUNZIONI
Relazione tra due insiemi:
R  X  Y  ( x, y) : x  X , y Y 
1
FUNZIONI
•L’insieme costituito dai primi elementi delle coppie
che definiscono R viene denominato dominio della
relazione e viene indicato con DR . Si ha DR  X
•Se DR  X la funzione viene chiamata
corrispondenza e viene indicata con C.
•L’insieme costituito dai secondi elementi delle coppie
che definiscono R viene denominato codominio della
relazione e viene indicato con il simbolo
CR
CR  Y
. Risulta
2
FUNZIONI
Una relazione R tra due insiemi non vuoti X e Y è
una funzione e viene indicata con f se soddisfa le
seguenti proprietà:
•ogni x di X ha almeno un’immagine in Y :
• x X , y  Y , tale che ( x, y)  R
•ogni x di X ha al più un’immagine in Y, ovvero se :
• x X tale che ( x, y1 )  R e ( x, y1 )  R allora
y1  y2
3
FUNZIONI
•Una funzione f può essere indicata con la scrittura:
• f : X Y
•Una funzione è comunemente indicata:
y  f (x)
•
•Si definisce:
graphf ( x)  ( x, y); x  X , y Y ; y  f ( x)
4
FUNZIONI
Esempio
La funzione parte intera di x:
y  f ( x)  x
5
FUNZIONI
Esempio
La funzione cubica:
y  f ( x)  x 3
100
50
-4
-2
0
2
x
4
-50
-100
6
FUNZIONI
•Una funzione f : X  Y si dice iniettiva se ad
elementi diversi di X corrispondono elementi diversi
di Y.
•Attenzione non si deve dire:
•Una funzione è iniettiva se ad ogni x corrisponde un
solo y.
•Questa è infatti la definizione di funzione!
7
FUNZIONI
Iniettiva
Non iniettiva
2
8
1.5
6
1
4
0.5
2
-4
-2
0
2
x
4
-4
-2
0
2
x
4
8
FUNZIONI
Una funzione f è suriettiva se ogni elemento di Y è
immagine di almeno un elemento di X.
x
x
9
FUNZIONI
Sia f: X  Y la funzione rappresentata da y=f(x). Si
definisce funzione inversa f 1 : Y  X la funzione che
associa ad ogni y la sua controimmagine x  f 1 ( y) .
Il grafico di una funzione e il grafico della funzione
inversa coincidono !
Esempio:
6
x  y 1 0
y  x 1
x  y 1
4
2
-4
-2
0
2
x
4
-2
-4
10
FUNZIONI
Teorema
Se una funzione f: X  Y
invertibile.
Esempio:
è biiettiva, allora è
y  ax
x  log a y
y  log a x
11
FUNZIONI
Si consideri una funzione f: X  Y
g :W  Z
e una funzione
Se il codominio della funzione f è un sottoinsieme
proprio o improprio del domino di g, si definisce
funzione composta di f e g la funzione
h g  f : X Z
espressa da
z  h( x)  g  f ( x)
12
FUNZIONI
Esempio
Si consideri la funzione f(x)=x+1
e la funzione g(x)=2x.
La funzione composta ottenuta applicando prima la f e
poi la g assume la forma:
z  h( x)  g  f ( x) : z  h( x)  2( x  1)  2 x  2
L’ordine di applicazione delle funzioni è importante,
Infatti se applichiamo prima la g e poi la f il risultato
diventa:
z  t ( x)  2 x  1
z  t ( x)  f g ( x)
:
13
FUNZIONI
x
x
14
FUNZIONI
15
FUNZIONI
16
FUNZIONI
17
FUNZIONI
18