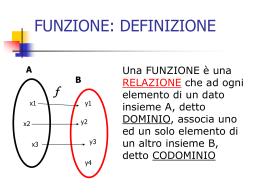
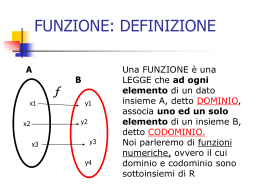
FUNZIONE: DEFINIZIONE
A
B
f
x1
y1
y2
x2
x3
y3
y4
Una FUNZIONE è una
LEGGE che ad ogni
elemento di un dato
insieme A, detto DOMINIO,
associa uno ed un solo
elemento di un insieme B,
detto CODOMINIO.
Noi parleremo di funzioni
numeriche, ovvero il cui
dominio e codominio sono
sottoinsiemi di R
FUNZIONE: DEFINIZIONE
A
B
f
x1
y1
y2
x2
x3
y3
y4
Si dice che y1 è IMMAGINE di x1
tramite la funzione f, y2 è immagine
di x2 attraverso la f e così via.
Si scrive y1=f(x1); y2=f(x2).
L’insieme degli elementi di B che
sono immagine di almeno un
elemento di A è detto INSIEME
DELLE IMMAGINI
Si dice che x1 è CONTROIMMAGINE
di y1 tramite f
FUNZIONE: DEFINIZIONE
Questa è una funzione
A
x1
B
A
x3
B
y1
x1
y2
x2
Questa non lo è
y3
y4
y1
y2
x2
x3
y3
y4
FUNZIONI
In altre parole puoi pensare ad una
funzione come ad una macchina
che prende in ingresso un valore x, lo
lavora, e poi butta fuori il valore di x
«lavorato», ovvero la y.
FUNZIONE: Rappresentazione
A
B
f
x1
y1
y2
x2
x3
Una funzione può essere
rappresentata in modo
insiemistico coi
diagrammi di Wenn: in
questo caso la freccia
indica la legge.
y3
y4
Molto intuitivo ma poco
pratico.
FUNZIONE: Rappresentazione
Q
y2
y1
P (x1, y1=f(x1))
x1
x2
Se sia A che B sono
sottoinsiemi dei numeri
reali, una funzione può
essere rappresentata
tramite il suo grafico,
ovvero l’insieme dei punti di
coordinate (x,y) tali che x
appartiene ad A e y è
l’immagine di x attraverso la
funzione
FUNZIONI: ELEMENTI
ESSENZIALI
Assegnare una funzione significa
assegnare:
1) Il suo dominio
2) La procedura , dato x elemento del
dominio, per determinare la sua
immagine f(x).
FUNZIONE: procedura
y  f ( x)  3x
y  f ( x)  senx
xy  2  0
2 Il modo con cui data x si
determina f(x) può
essere fornito tramite
un’equazione nelle
lettere x e y, sia in
forma esplicita y=f(x),
che implicita F(x,y)=0
FUNZIONE: Rappresentazione
 3x se x  2
y
 x  2 se x  2
2
Una funzione può
anche essere
definita PER CASI,
ovvero possono
esserci modi
differenti
per determinare f(x)
a seconda dei valori
di x
FUNZIONE: valore assoluto
 x
| x | 
 x
x0
x0
Un esempio è la
funzione VALORE
ASSOLUTO
y=|x|
FUNZIONE: funzione segno
1 x0
sgn( x)  
 1 x  0
1
-1
Un altro è la
funzione segno
FUNZIONE: parte intera
INT ( x)  n n  x  n  1 n Z
3
La funzione
“parte intera di
x”, che ad ogni
numero associa
la sua parte
intera
2
1
0
1
2
3
4
FUNZIONE: iniettiva
A
B
f
x1
y1
y2
x2
x3
x4
y3
y4
Una funzione si dice INIETTIVA
se:
ogni elemento di B ha al più
una controimmagine in A,
ovvero se:
ad elementi distinti del
dominio essa associa elementi
distinti del codominio
f non è iniettiva perché y3 ha due
controimmagini: x3 e x4
FUNZIONE: suriettiva
A
B
f
x1
y1
y2
x2
x3
x4
y3
y4
Una funzione si dice SURIETTIVA
se:
ogni elemento di B ha almeno
una controimmagine in A
ovvero se:
l’insieme delle immagini
coincide con il codominio
f non è suriettiva perché y4 non ha
controimmagine
FUNZIONE: biunivoca
A
B
f
x1
y1
y2
x2
x3
x4
y3
y4
Una funzione si dice
BIUNIVOCA se è
iniettiva e suriettiva
FUNZIONE: classificazione
FUNZIONI ALGEBRICHE: sono quelle
nella cui espressione si trovano solo
le quattro operazioni, l’elevamento a
potenza, l’estrazione di radice
FUNZIONI TRASCENDENTI: funzione
esponenziale e logaritmica, le funzioni
goniometriche e tutte le loro
combinazioni
FUNZIONE: classificazione
FUNZIONI RAZIONALI: sono quelle in
cui l’incognita x non compare sotto
segno di radice
FUNZIONI IRRAZIONALI: sono quelle
in cui la x compare sotto segno di
radice
FUNZIONE: classificazione
FUNZIONI INTERE: sono quelle in cui
la x compare solo al numeratore
FUNZIONI FRATTE: sono quelle in cui
la x compare al denominatore
FUNZIONE: ricerca del dominio
Il dominio di una funzione è il più
grande sottoinsieme dei numeri reali
x, per i quali la procedura che
definisce la funzione ha significato,
ovvero per i quali si può calcolare la
f(x).
La ricerca del dominio dipende dal
tipo di funzione
FUNZIONE: ricerca del dominio
• in una funzione FRATTA bisogna
porre il denominatore diverso da zero
• in una funzione IRRAZIONALE con
indice pari bisogna porre il radicando
maggiore o uguale a zero
• in una funzione logaritmica bisogna
porre l’argomento maggiore di zero
• nella funzione tangente l’argomento
deve essere diverso da /2+k
FUNZIONE: crescente
f(x2)
f(x1)
x1
x2
Intuitivamente,
una funzione è
CRESCENTE
quando,
all’aumentare
del valore di x,
aumenta anche
il valore di y
FUNZIONE: crescente
Rigorosamente, una funzione si dice
CRESCENTE in un dato intervallo I
del dominio se:
per ogni coppia di valori x1 e x2
appartenenti ad I, se x2  x1
allora si ha che f ( x2 )  f ( x1 )
FUNZIONE: decrescente
Analogamente, una funzione si dice
DECRESCENTE in un dato intervallo I del
dominio se:
per ogni coppia di valori x1 e x2
appartenenti ad I, se
allora si ha che
x2  x1
f ( x2 )  f ( x1 )
FUNZIONE: monotonia
Una funzione che, in un intervallo, risulti
o crescente o decrescente, si dice
MONOTONA
in tale intervallo.
FUNZIONE: pari
Una funzione si dice PARI se:
1)
2)
x  domf   x  domf
f ( x)  f ( x)
Il grafico di una funzione pari
è simmetrico rispetto
all’asse y
FUNZIONE: dispari
Una funzione si dice DISPARI
se:
1)
x  domf   x  domf
2)
f ( x)   f ( x)
Il grafico di una funzione
dispari è simmetrico rispetto
all’origine degli assi
FUNZIONE: periodica
Una funzione si dice
PERIODICA se:
esiste un numero T>0, tale
che
f ( x  T )  f ( x)
per ogni x del dominio.
Il minore dei valori di T si
dice PERIODO
FUNZIONE: funzione invertibile
Sia f una funzione iniettiva.
A
B
f-1
x1
1
y1
y2
x2
x3
Allora f è INVERTIBILE
f
ovvero
le legge che ad ogni
elemento di imf associa la
sua controimmagine è una
funzione. Tale funzione è
detta FUNZIONE INVERSA e
si indica con il simbolo
y3
y4
f
1
FUNZIONE: funzione inversa
Osserviamo che :
1
Il dominio di f
coincide con imf .
1
Mentre im f coincide con il dominio di f.
Questa osservazione può essere sfruttata
per trovare l’insieme delle immagini di
una funzione , ovviamente se essa è
invertibile.
FUNZIONE: invertibilità e
monotonia
f(x2)
f(x1)
x1
x2
Se una funzione è
crescente allora è
anche invertibile;
infatti non si
verifica mai che
assuma due volte
lo stesso valore
perciò è
sicuramente
iniettiva
FUNZIONE: invertibilità e
monotonia
Lo stesso se la
funzione è
decrescente.
Quindi:
f(x1)
f(x2)
x1
x2
SE UNA FUNZIONE
E’ MONOTONA
ALLORA E’
INVERTIBILE
FUNZIONE: invertibilità e
monotonia
Attenzione : non
vale il viceversa!
Ad esempio la
funzione nel
grafico non è
monotona, ma è
invertibile.
FUNZIONE: funzione invertibile
N.B: Anche se una funzione non è
invertibile su tutto il suo dominio, lo può
diventare se il dominio viene ristretto.
Ad esempio, la funzione y  x
non è invertibile, ma lo sono la sue
restrizioni all’intervallo 0; o
all’intervallo   : 0
2
FUNZIONE: funzioni inverse
Funzione Restrizione
del dominio*
y=x2
x≥0
Inversa
Dominio
y=√x
x≥0
y=x3
R
y=3√x
R
y=lnx
x>0
y=ex
R
y=senx
-/2≤x≤/2
y=arcsenx
-1≤x≤1
y=cosx
0≤x≤
y=arccos
-1≤x≤1
y=tgx
-/2≤x≤/2
y=arctgx
R
FUNZIONE: ricerca dell’inversa
La funzione inversa si trova risolvendo
l’equazione y=f(x) in funzione di x,
ovvero trovando x in funzione di y.
FUNZIONE: grafico dell’inversa
Il grafico di una funzione f è composto da
punti di coordinate (x,y), mentre quello
1
f
della funzione
è composto da punti
di coordinate (y,x).
1
f
Allora il grafico di f e quello di
sono
l’uno il simmetrico dell’altro rispetto
alla bisettrice del primo e terzo
quadrante.
FUNZIONE: funzioni uguali
Due funzioni f e g sono uguali se :
1) Hanno lo stesso dominio (domf= domg)
2) Hanno la stessa procedura (f(x)= g(x))
x 1
x 1
Rispondi : le funzioni f ( x)  x  2 e g ( x)  x  2
sono uguali? Perché?
FUNZIONE: composizione
Sia f: A 
B che x y e sia g: B  C che
y z .
Allora è possibile definire la funzione
g◦f: A
C
che
x z
FUNZIONE: composte
La composta si può così indicare
g(f(x))
oppure
g◦f(x)
Grafici: esponenziale
Grafici: logaritmo naturale
Grafici: seno
Grafici: arcoseno
Grafici: coseno
Grafici: arcocoseno
Grafici: tangente
Grafici: arcotangente
Grafici: quadratica
Grafici: cubica
Grafici: radice quadrata