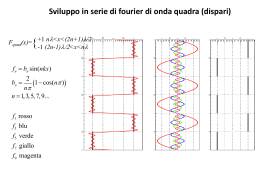
H* Coefficienti dell'onda quadra: *L
1 1 -ä n Π x
c@n_D :=
âx
à ã
2 0
H* Se li accorpo con segno opposto: *L
FullSimplifyAc@nD ãä n Π x + c@- nD ã-ä n Π x E
H* Se prendo quelli pari: *L
FullSimplifyAc@nD ãä n Π x + c@- nD ã-ä n Π x , 8Mod@n, 2D Š 0<E
H* Se prendo quelli dispari: *L
FullSimplifyAc@nD ãä n Π x + c@- nD ã-ä n Π x , 8Mod@n, 2D Š 1<E
- Sin@n Π H- 1 + xLD + Sin@n Π xD
nΠ
0
2 Sin@n Π xD
nΠ
H* Devo usare solo quelli pari: *L
1
2 Sin@n Π xD
10
PlotB + â Mod@n, 2D
, 8x, - 2, 2<F
n=1
2
nΠ
1.0
0.8
0.6
0.4
0.2
-2
-1
1
2
2
Fourier.nb
H* Passiamo dalla serie alla trasformata: *L
T
Π
Π
1
+¥
f@tD = LimitBâ
f@tD ã-ä n T t â t ãä n T x , 8T ® + ¥<F
à
n=-¥ 2 T
-T
T
Π
Π
1
+¥
LimitBâ
f@tD ã-ä n T t ãä n T x â t , 8T ® + ¥<F
à
n=-¥ 2 T -T
T
Π
Π
1
+¥
LimitBà â
f@tD ãä n T x ã-ä n T t â t , 8T ® + ¥<F
n=-¥ 2 T
-T
H* Definiamo f@tD=0 per t >T: *L
+¥
Π
Π
1
+¥
LimitBà
f@tD ãä n T x ã-ä n T t â t , 8T ® + ¥<F
â
n=-¥
2T
-¥
Π
H* A questo punto definiamo n T = Ωn e studiamo la serie: *L
â
+¥
1
1
â
+¥
Ωn
f@tD ãä Ωn x
n=-¥ n
2T
2Π
Π
Π
Π
H* Ora, essendo Ωn+1 -Ωn = Hn+1L T -n T = T e chiamando quest'ultimo DΩ: *L
n=-¥
f@tD ãä Ωn x =
f@tD ãä Ωn x DΩ
â
n=-¥
2Π
H* Reisnerendo la serie nell'integrale: *L
+¥
1
+¥
LimitBà Iâ
f@tD ãä Ωn x DΩM ã-ä Ωn t â t , 8T ® + ¥<F
n=-¥
2Π
-¥
+¥
1
+¥
LimitBâ
f@tD ã-ä Ωn t â t ãä Ωn x DΩ, 8T ® + ¥<F
à
n=-¥
2Π
-¥
H* Diamo un nome all'integrale: *L
+¥
`
-ä Ω t
à f@tD ã n â t = f@Ωn D
1
+¥
H* Riscriviamo e notiamo che il limite della serie diventa un integrale: *L
1
+¥
`
LimitAâ
f@Ωn D ãä Ωn x DΩ, 8T ® + ¥<E
n=-¥
2Π
+¥ `
1
ä Ωx
f@tD =
âΩ
à f@ΩD ã
2 Π -¥
H* in cui: *L
+¥
`
f@ΩD = à f@tD ã-ä Ωt â t
-¥
H* rappresenta la trasformata di Fourier e permette
di passare adl dominio del tempo a quello delle frequenze,
mentre la precedente rappresenta la trasformata inversa. *L
-¥