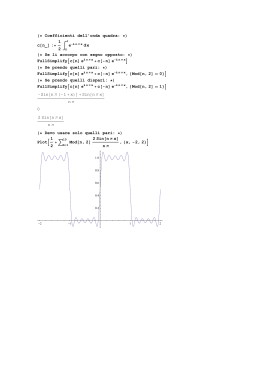
Strumentazione per bioimmagini
Operazioni elementari, Trasformata di Fourier e Trasformata Radon
Proiezioni
pθ(x’)
x’
y
y’
θ
f(x,y)
x
 cos
x , y T  
 sin 

 sin  
 x, y T

cos 
Ogni linea ortogonale a  e distante tk dall’origine ha
espressione parametrica:
x cos( )  y sin(  )  tk
Trasformata di Radon
pθ(x’)
x’
y
y’
θ
f(x,y)
x
p ( x)    f ( x, y ) ( x cos( )  y sin(  )  x' )dxdy
La notazione evidenzia che l’angolo e’ un
parametro, piu’ che una variabile indipendente
Trasformata Radon: esempio
p0 ( x' )
p45 ( x' )
f(x,y)
p90 ( x' )
Trasformata di Radon: sinogramma
Trasformata Radon
•Esempi:
RT
“sinogramma”
x’
θ
Teorema della sezione centrale
“La trasformata di Fourier della proiezione p (trasformata di Radon)
di f(x,y) dato θ, è pari alla trasformata di Fourier 2D di f(x,y) valutata su
una retta passante per l’origine delle frequenze con angolo θ.”
F (u , v)  F ( f ( x, y ))
P ( )  F ( p ( x' ))
v
pθ(x’)
F(u,v)
y
y’
Pθ(w)
θ
θ
f(x,y)
u
FT 1D
x
Teorema della sezione centrale
• Si dimostra a partire dalla F(u,v) valutata lungo la retta w di direzione θ
nel piano delle frequenze:
F  ,    F u, v 
w,
 F  cos  ,  sin   
  f ( x, y )e j 2  x cos  y sin  dxdy
• cambio di variabili: x,y  x’,y’ (matrice di rotazione)
 

j 2x
j 2x





f ( x , y )dy  e
dx   p x e
dx  P  
F ,   P  
Teorema della sezione centrale
•Attraverso la RT e’ possibile stimare la F(u,v).
•La FT della trasformata Radon campiona lo spazio delle frequenze
con un reticolo polare.
•L’inversione della RT attraverso l’inversione della FT richiede la
ricostruzione del reticolo ortogonale
le alte frequenze vengono interpolate male
con conseguente bassa resa dei dettagli
u
v
u
interpolazione
v
L’idea della ricostruzione filtrata
• L’idea più semplice è che data una frequenza w, ad essa
venga associato un peso proporzionale alla distanza dai
campioni più vicini con lo stesso modulo |w|.
v
u
• Date K proiezioni, il peso per un campione w è 2|w|/K