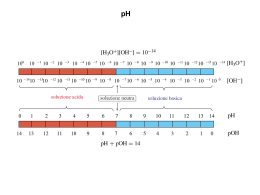
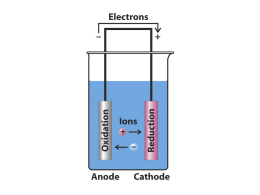
Chimica
(a.a. 2011/2012, 6CFU)
Equilibri ionici in soluzione acquosa (I parte):
Acidi e Basi: la teoria di Brönsted-Lowry
Forza relativa di acidi e basi
Autoionizzazione (autodissociazione) dell’acqua
Il pH e il pOH
Calcolo del pH di soluzioni di acidi forti e basi forti
Acidi deboli La costante di acidità Ka
Basi deboli: La costante di basicità Kb
Calcolo del pH per un acido debole monovalente (monoprotico)
Calcolo del pH per un base debole monovalente
Che cosa è un acido?
E una base?
ACIDI E BASI NELLA VITA
QUOTIDIANA
Acidi
Basi
Molti dei prodotti, normalmente usati in casa, presentano caratteristiche
acide o basiche. Ne sono esempi: saponi, detersivi, medicine e alimenti
Etimologia: Acidi e Basi
Acido è una parola che deriva dal latino
“acetum” (aceto). Col tempo la parola si è
estesa a tutte le sostanze che hanno un
analogo sapore “acidulo” (aspro).
Basi o alcali (dall’arabo al kali = la cenere delle
piante) sono le sostanze in grado di neutralizzare
gli acidi.
Qual è la definizione di acido e di base dal
punto di vista della chimica?
La storia ……………….…
Antoine Lavoisier
1743-1794
Humpry Davy
1778-1829
Lavoisier definì gli acidi come combinazioni di radicali ed ossigeno (oxys
genes = generatore d’acido), e le basi come una combinazione di metalli ed
ossigeno. La sua idea fu in genere accettata, nonostante che acidi come
l’acido cloridrico fossero noti da secoli. Si credeva allora che il cloro fosse
un ossido piuttosto che un elemento. Nel 1809 Gay-Lussac (1778-1850), in
collaborazione con Trénard (1777-1857) trovò che i cloruri, allora chiamati
muriati, non contenevano ossigeno. Comunque essi erano talmente persuasi
della validità delle idee di Lavoisier che preferirono dubitare dei propri
risultati piuttosto che proporre il nuovo concetto. Fu il chimico inglese
Humpry Davy (1778-1829) a cambiare la teoria acido-base provando che il
cloro era un elemento e che l’acido cloridrico non conteneva ossigeno. Egli
considerava l’idrogeno come il principio degli acidi (1810) e la sua teoria fu
accettata in breve tempo.
Un approccio moderno al problema è stato possibile solo dopo che
Arrhenius propose la sua teoria della dissociazione elettrolitica, che
includeva il concetto di elettroliti forti, cioè, sali, acidi e basi.
Egli proclamò le sue convinzioni all’Accademia Svedese delle scienze nel
1883 e pubblicò la sua teoria nel 1887. Secondo Arrhenius, un acido si
dissocia in ioni idrogeno ed alcuni anioni, mentre una base si dissocia
in ioni idrossido e nei corrispondenti cationi. Il concetto di Arrhenius
forniva anche una spiegazione delle diverse forze dei diversi acidi, basate
sui loro differenti gradi di dissociazione.
Svante August Arrhenius
Wijk (Svezia), 1859 – Stoccolma, 1927
Premio Nobel per la Chimica 1903
……….. la storia ……………….…
Johannes Nicolaus BrØnsted
1879-1947
Thomas Martin Lowry
1874-1936
Sorsero, tuttavia, ulteriori difficoltà nel
tentativo di spiegare l’acidità delle soluzioni
organiche. Una soluzione di ammoniaca in etere
esibisce delle proprietà basiche, ma si può
dimostrare che in una tale soluzione non esiste lo
ione idrossido. Arthur Lapworth (1872-1941),
professore dell’Università di Manchester,
insegnante di chimica organica, fisica ed
inorganica, descrisse gli acidi come donatori di
ioni idrogeno. T. M. Lowry (1874-1936) era uno
dei suoi allievi. Lui ed il professore danese Johann
N. Brønsted (1879-1947) svilupparono
indipendentemente le idee di Lapworth di acidi e
basi in quella che è attualmente chiamata
teoria di Brønsted- Lowry (1923).
Acidi e Basi
Definizione di Arrhenius (1887): acidi e
basi sono composti che in acqua danno luogo
a dissociazione elettrolitica:
Acido → H+(aq) + ...
Base → OH-(aq) + ...
Gli acidi e le basi secondo la teoria di
Arrhenius:
Le sostanze che dissociandosi in acqua dando ioni idrogeno
(protoni) sono acide:
HCl
H2O
→
H+ + Cl-
(H+ raggio ionico di 10-15 m!, esso in soluzione acquosa si trova come ione
idrossonio: H3O+ ovvero H(H2O)+n con 1≤n≤7, n numero intero)
Gli acidi e le basi secondo la teoria di
Arrhenius:
HCl
H2O
→
H+ + ClH2O
H3O+
Gli acidi e le basi secondo la teoria di
Arrhenius:
Le sostanze che dissociandosi in acqua danno ioni idrossido
(ossidrile) sono basiche:
H2O
NaOH → Na+ + OH-
Arrhenius distinse poi gli acidi e le basi a seconda della loro
forza.
Un acido forte è una sostanza che in acqua si ionizza
completamente per dare ioni H+ (es. HCl):
HCl(aq)
→
H2O
H+(aq) + Cl-(aq)
Una base forte è una sostanza che in acqua si ionizza
completamente per dare ioni OH- (es. NaOH):
NaOH(aq)
→
H2O
Na+(aq) + OH-(aq)
Acidi e basi deboli non sono completamente
soluzione ma danno luogo ad un equilibrio
CH3COOH(aq)
Acido acetico
H2O
ionizzati
H+(aq) + CH3COO-(aq)
in
Nonostante i suoi primi successi e la sua utilità, la teoria di Arrhenius
ha dei limiti.
Il primo problema è di natura formale ed emerse dopo i primi studi
sull’atomo. Lo ione H+ è un protone semplice e non può esistere in
acqua come tale, ma solo legato ad una molecola di acqua sottoforma
di ione H3O+ in cui lo ione H+ è legato all’ossigeno (grazie al doppietto
solitario: si forma un vero è proprio legame covalente) dell’acqua
(talvolta questo legame è detto dativo, tuttavia questa dizione è in
disuso, oltre ad essere formalmente errata, nella chimica moderna).
Questo può essere facilmente preso in considerazione:
HCl(aq) +H2O(l)
→
CH3COOH(aq)+H2O(l)
H3O+(aq) + Cl-(aq)
H3O+(aq) + CH3COO-(aq)
Inoltre la teoria di Arrhenius è limitata a soluzioni acquose e non
considera basiche sostanze che non contengono ioni OH- (ad esempio
NH3).
Lo Ione Idrossonio
(detto anche idronio o ossonio )
• Il catione idrogeno, un protone nudo, è una particella caratterizzata da un’elevata
densità di carica (è, infatti, molto piccolo) e non esiste come tale in soluzione. Esso
tende ad interagire con l’atomo di ossigeno di una molecola di acqua per formare lo
ione H3O+ o idrossonio.
•Lo ione idrossonio, a sua volta, interagisce con le molecole d’acqua che lo
circondano formando altre specie: H5O2+, H7O3+, H9O4+
H(H2O)+4
• Questo fenomeno, che può essere dedotto da misure di conducibilità, è
DETTO IDRATAZIONE
• Il protone idratato si indica come H+(aq)
Insufficienza
della definizione di Arrhenius:
Molte basi, come per esempio NH3,
non possono formare OH-(aq) per
semplice dissociazione elettrolitica.
La reazione acido-base deve essere
di tipo diverso !!!!
Secondo la teoria di Br
Brø
ønsted
nsted-Lowry (1923
1923):
):
Un ACIDO è una qualunque sostanza, che è capace di
donare uno ione idrogeno (protone) ad un altra
sostanza in una reazione chimica.
Una BASE è una sostanza che accetta lo ione
idrogeno (protone) dall'acido.
N.B.: questa definizione non è vincolata alla presenza
del
solvente;
una
reazione
acido-base
può
avvenire quindi in un solvente qualunque, in assenza di
solvente ed in qualunque stato di aggregazione delle
sostanze.
Noi, tuttavia , tratteremo solo soluzioni acquose!
EQUILIBRI ACIDO-BASE
Secondo Brønsted e Lowry
un acido è una sostanza capace di cedere uno o più protoni
una base è una sostanza capace di acquistarli
Si introduce così il concetto di sistema acido-base nel quale
l’acido manifesta le sue proprietà qualora sia disponibile una
sostanza (la base) che renda possibile il trasferimento di protoni
sistema coniugato acido base (1)
Acido1
+
Base2
Base1
+
sistema coniugato acido base (2)
Acido2
EQUILIBRI ACIDO-BASE
Forza di acidi e basi
Secondo la teoria di Brønsted e Lowry una delle due
sostanze che partecipano all’equilibrio acido-base può essere
il solvente stesso, ad esempio l’acqua
La forza degli acidi e delle basi è determinata sulla base
del solvente nel quale si instaura l’equilibrio
sistema coniugato acido base (1)
Acido1
+
H2O
Base1
+
H3O+
sistema coniugato acido base (2)
Tanto maggiore la capacità dell’acido di trasferire il proprio
protone all’acqua, tanto più forte sarà l’acido
(riassumendo
riassumendo))
Definizione di Br
Brø
ønsted e Lowry
Acido = donatore di protoni (H+)
Base = accettore di protoni (H+)
Poiché il protone non può esistere isolato, in soluzione, un acido si
manifesta tale solo se è in presenza di una base che possa accettare
protoni, così come una base si manifesta tale solo in presenza di un acido
che possa fornire protoni: è perciò più corretto parlare di sistemi acido-
base che di acidi e basi singolarmente.
“coppie acidoacido-base coniugati”
coniugati”
ione nitrito
acido nitroso
ione idrossonio
HNO2(aq
aq)) + H2O(
O(ll) ⇄ NO2-(aq
aq)) + H3O+(aq
aq))
acido 1
base 2
base 1
NO2- base coniugata dell’acido HNO2 Posso
H2O base coniugata dell’acido
H3O+
anche
dire
acido 2
HNO2 acido coniugato della base NO2H3O+ acido coniugato della base H2O
HNO2 acido coniugato della base NO2oppure
NO2- base coniugata dell’ acido HNO2
In generale coppia coniugata acido
acido-base:
HNO2/NO2-
H2O base coniugata dell’acido H3O+
oppure
H3O+ acido coniugato della base H2O
In generale coppia coniugata acido
acido-base:
H3O+/H2O
Il caso dell’ammoniaca (NH3) :
ione ammonio
ammoniaca
ione ossidrile
NH3(aq
aq)) + H2O(
O(ll) ⇄ NH4+(aq
aq)) + OH-(aq
aq))
base 1
acido 2
acido 1
base 2
NH4+ acido coniugato della base NH3
oppure
NH3 base coniugata dell’ acido NH4+
In generale coppia coniugata acido
acido-base:
NH4+/NH3
OH- base coniugata dell’acido H2O
oppure
H2O acido coniugato della base OHIn generale coppia coniugata acido
acido-base:
H2O/OH-
Una specie può comportarsi da acido o da base a seconda della
specie con cui viene fatta reagire. Ad esempio H2O si comporta
da base con HCl (accetta un protone formando H3O+), ma si
comporta da acido con NH3 (cede il protone formando OH-).
Specie di questo tipo, che possono agire sia come acido che
come base in dipendenza dell’altro reagente, vengono dette
anfiprotiche (o anfotere).
La teoria di Brønsted e Lowry è più generale della teoria di
Arrhenius. In particolare:
- Una base è una sostanza che accetta protoni (lo ione OH-,
che secondo Arrhenius una sostanza deve necessariamente
possedere per essere una base, è solo un esempio di base);
- Acidi e basi possono essere sia sostanze molecolari sia ioni;
- Possiamo avere solventi diversi dall’acqua;
- Alcune sostanze possono agire da acido o da base a seconda
della specie con cui reagiscono;
Forza relativa di acidi e basi
La forza relativa di un acido (o di una base) può essere
considerata in funzione della loro tendenza a perdere
(accettare) un protone. Gli acidi più forti sono quelli che
perdono più facilmente i loro protoni. Analogamente le basi più
forti sono quelle che accettano un protone più facilmente.
Un acido forte è una sostanza che in acqua è completamente
ionizzato:
HCl(aq) + H2O(l) → H3O+(aq) + Cl-(aq)
acido
base
acido
base
La reazione è spostata completamente verso destra, per cui
l’acido cloridrico è un acido forte. Se si considera la reazione
inversa, questa avviene in piccolissima parte (praticamente
non avviene). In essa lo ione Cl- agisce come base accettando
un protone dall’acido H3O+, ma è una base estremamente
debole.
HCl(aq) + H2O(l) → H3O+(aq) + Cl-(aq)
acido
base
acido
base
più forte
più debole
Questa reazione si può considerare anche in funzione della
forza relativa tra HCl e H3O+. HCl perde il protone più
facilmente di H3O+ ed è quindi un acido più forte e la
reazione è spostata verso destra.
Se consideriamo la ionizzazione dell’acido acetico:
CH3COOH(aq) +H2O(l)
H3O+(aq) + CH3COO-(aq)
acido
acido
più forte
più debole
Sperimentalmente si vede che solo l’1% delle molecole di
CH3COOH sono ionizzate. Questo vuol dire che H3O+ è un acido
più forte di CH3COOH. L’equilibrio è spostato verso sinistra.
CH3COO- è la base coniugata di CH3COOH. Poiché l’equilibrio è
spostato verso sinistra questo vuol dire CH3COO- è sì una base
debole ma sicuramente più forte di H2O.
In generale in una reazione acido-base la reazione è spostata
nella direzione dal più forte al più debole membro della coppia
coniugata acido-base.
Se consideriamo la ionizzazione dell’acido fluoridrico:
HF(aq) +H2O(l)
acido
più debole
H3O+(aq) + F-(aq)
acido
più forte
Qui solo il 3% delle molecole di HF sono ionizzate. Questo vuol
dire che HF è un acido più debole di H3O+, ma è più forte di
CH3COOH. F-, la base coniugata di HF, è una base più forte di
H2O, ma più debole di CH3COO-.
Gli acidi più forti hanno le basi coniugate più deboli, e le
basi più forti hanno gli acidi coniugati più deboli.
In base ai dati precedenti possiamo stabilire la seguente scala
di acidità:
HCl>H3O+>HF>CH3COOH
ACIDI FORTI ed ACIDI DEBOLI
Si può quindi scrivere la seguente tabella
ACIDI FORTI ed ACIDI DEBOLI
In realtà nella tabella HNO3, H2SO4, HCl, HBr, HI e HClO4 sono tutti acidi forti
(=completamente dissociati in acqua) ed è quindi evidente che per stabilire la
forza relativa di questi acidi occorre procedere diversamente da quanto fatto in
precedenza.
Gli acidi precedenti, sciolti in acqua, sono tutti ionizzati al
100%, ma se usiamo un solvente meno basico dell’acqua
(come, ad esempio, l’etere etilico CH3CH2OCH2CH3) si può
notare una differenza.
Per esempio né HCl, né HI sono completamente ionizzati, ma
si trova che HI è ionizzato in percentuale maggiore rispetto
ad HCl ed è quindi un acido più forte.
Poiché per gli acidi forti la forza in acqua sembra essere la
stessa si parla di EFFETTO LIVELLANTE DELL’ACQUA sugli
acidi forti.
Riassumendo …
• In una reazione acido-base la direzione favorita della reazione è dal
più forte al più debole membro della coppia coniugata acido-base:
HCl + OHCl+
H2O
Acido (1)
forte
Base (2)
forte
H2O +
Acido (1)
debole
I-
Base (2)
debole
Base (1)
debole
OHBase (1)
forte
Acido (2)
debole
+
HI
Acido (2)
forte
• IL “FORTE” SPOSTA SEMPRE IL “DEBOLE”
• PIÙ FORTE È UN ACIDO E PIÙ DEBOLE È LA SUA BASE
CONIUGATA E VICEVERSA
• In acqua HCl e HClO4 sono entrambi completamente dissociati: l’acqua ha un
EFFETTO LIVELLANTE su questi acidi. Per determinare quale sia più forte
bisogna usare un solvente che sia una base più debole dell’acqua: in etere
dietilico HClO4 è dissociato completamente mentre HCl no (quindi, HClO4 è più
forte)
L’ACQUA:: ACIDO o BASE
L’ACQUA
L’acqua è una sostanza ANFIPROTICA = può comportarsi sia da
acido che da base (di Brønsted-Lowry):
ANFOTERA = sostanza che può comportarsi sia da acido che da base
L’autoprotolisi
L’
autoprotolisi dell’acqua
Il prodotto della concentrazione di OH- per quella dello ione H3O+ in
una qualunque soluzione acquosa è costante a temperatura costante.
Esso corrisponde alla costante dell'equilibrio di autoprotolisi (o
autodissociazione o autoionizzazione) dell'acqua che a 25°C è uguale a
1,0 x 10-14.
H2O(l) + H2O(l) ⇄ H3O+(aq
aq)) + OH-(aq)
Per l'equilibrio vale la seguente costante:
+
−
K W = [ H 3O ] ⋅ [OH ] = 1,0 ⋅ 10
−14
detto prodotto ionico dell’acqua
Il pH e la sua scala: il grado di acidità di una soluzione acquosa
non viene valutato direttamente con il valore della concentrazione
molare (attività) dello ione H+ (cioè H3O+) ma , per agilità di calcolo,
come il suo cologaritmo (in base 10), indicato con il simbolo pH:
pH = -log10 a H3O+ = -log10 [H3O+]
pOH = -log10 [OH-]
pH + pOH = pKw = 14
Soluzioni basiche
pH
basicità crescente
0 1
2
3
4
5 6 7 8 9 10 11 12 13 14
14 13 12 11 10 9 8 7
6
5
acidità crescente
Soluzioni acide
4
3
2
1 0
pOH
Il concetto di pH nacque all’inizio (1909) del secolo scorso in una fabbrica di birra.
Storia e mistero di un simbolo
Ph
⇓
pH +
⇓
pH
⇓
pH
Originariamente Sørensen
utilizzò come simbolo "Ph"
versione originale in un
articolo in francese
tipografi tedeschi
tipografi americani (anni ‘20)
attuale scrittura in linea
S.V.L. Sørensen 1868-1939
(chimico danese)
Direttore del prestigioso Laboratorio Carlsberg, fondato dall'industriale danese che creò l'omonima birreria
Sørensen studiando l’azione degli acidi sulla catalisi enzimatica, dovendo
esprimere con numeri semplici il grado di acidità propose l’uso del
pH = - log [H+]
N.B. il simbolo p non è un reale operatore matematico
ma dobbiamo solo ricordare che corrispondete a –log10.
…il pH e la sua scala…
Una soluzione è definita:
Neutra: quando il pH assume esattamente il valore 7
Acida: quando il pH assume valori minori di 7
Basica: quando il pH assume valori maggiori di 7
Nella seguente figura vengono riportati i valori di pH di alcune soluzioni comuni:
…il pH e la sua scala…
La scala qui mostrata va da pH 0 a
14.
Sono possibili valori leggermente
negativi di pH così come valori di
pH più alti di 14:
• pH<0: soluzioni estremamente
acide.
• pH>14 : soluzioni estremamente
basiche.
[OH-]
[H3O+]
pOH
pH
Autoprotonazione dell’acqua
2 H2O(l)
H3O+(aq) + OH-(aq)
Kw = [H3O+]· [OH-]
A 25°C si ha Kw = 10-14
Soluzione neutra: [H3O+] = [OH-]
Soluzione acida: [H3O+] > [OH-]
Soluzione basica: [H3O+] < [OH-]
Kw =
+
[H3O ]·[OH ]
Soluzione neutra
neutra::
[H 3O + ] = [OH − ] = K w
Soluzione acida
acida:: [H 3O + ] > K w ; [OH − ] < K w
+
−
Soluzione basica
basica:: [H 3O ] < K w ; [OH ] > K w
a 25°
25°C
[H3O+] > [OH-]
[H3O+]
100
10-1
10-2
10-3
10-4
10-5
Kw
10-6
soluzione acida
[H3O+] > 10-7
[OH-] < 10-7
[H3O+] < [OH-]
10-7
10-8
10-9
10-10
10-11
10-12
10-13
10-14
soluzione basica
soluzione
neutra
[H3O+] = [OH-] = 10-7
[H3O+] < 10-7
[OH-] > 10-7
L’autoprotonazione
dell’acqua
è
una
reazione endotermica (assorbe calore)
H3O+(aq) + OH-(aq)
2 H2O(l)
+
−
Kw = [H3O ] [OH ]
∆H° > 0
Perché?::
Perché?
Nella lezione #12 abbiamo dimostrato che la reazione
neutralizzazione)) è esotermica (∆H<
H<0
0)
inversa (neutralizzazione
T > 25°C
10-13
lnKw
∆H° > 0
25°C
10-14
10-15
10-16
T < 25°C
1/T
Soluzione neutra:
1/T
[H3O+ ] = [OH− ] = Kw ; pH = −log10Kw
A 25°
25°C: pH = 7; a T < 25°
25°C: pH > 7; a T > 25°
25°C: pH < 7
T( °C)
0
10
20
25
30
40
50
60
Kw
1,14 · 10-15
2,92 · 10-15
6,81 · 10-15
1,01 · 10-14
1,47 · 10-14
2,92 · 10-14
5,47 · 10-14
9,61 · 10-14
pH
7,47
7,27
7,08
7,00
6,92
6,77
6,63
6,51
Calcolo del pH di soluzioni di acidi forti e basi forti
Comuni acidi forti e basi forti
Acidi
Basi
HCl
LiOH
HBr
NaOH
HI
KOH
HClO4
RbOH
HNO3
CsOH
H2SO4
*
Mg(OH)2
Ca(OH)2
Sr(OH)2
Ba(OH)2
*H2SO4 ionizza in due stadi distinti ed è un acido forte
solo nella prima ionizzazione
Calcolo del pH di soluzioni di acidi forti
Si disciolga un acido forte, per esempio HCl, in acqua,
questo si dissocia completamente secondo l’equazione:
HCl(aq) + H2O(l) → H3O+(aq) + Cl-(aq)
nella soluzione è presente
autodissociazione dell’acqua:
anche
l’equilibrio
di
2 H2O(l) ⇄ H3O+(aq) +OH- (aq)
che pure fornisce ioni H3O+. Nella maggior parete dei
casi, tuttavia, questi ultimi sono trascurabili nei
confronti di quelli che derivano dalla dissociazione
(completa) dell’acido.
Calcolo del pH di soluzioni di acidi forti
Si calcoli il pH di una soluzione 0,10 M di HNO3
HNO3 è un acido forte, quindi in H2O si dissocia completamente:
HNO3(aq) + H2O(l) → NO3-(aq) + H3O+(aq)
[H3O+] derivante dall’acido = [HNO3]= 0,100 M
pH = -log10[H3O+] = -log10 [0,10] = 1
Il pH risultante è acido
Si calcolino il pH ed il pOH di una soluzione
acquosa 1,0·10-4 M di HClO4
HClO4 è un acido forte, quindi in H2O si dissocia
completamente:
HClO4(aq) + H2O(l) → ClO4-(aq) + H3O+(aq)
[H3O+] derivante dall’acido = [HClO4]= 1,0 · 10-4 M
pH = -log [1,0 · 10-4] = 4
poiché [H3O+]·[OH-] =KW= 1,0 ·10-14 M risulta che:
[OH-] = 1,0 · 10-14/1,0 · 10-4 = 1,0 ·10-10 M
pOH = 10,0
Si noti che pH + pOH = pKw= 14
Nel problema non si è tenuto conto del contributo degli
ioni H3O+ derivanti dalla dissociazione dell’H2O
Si verifica a posteriori che l’approssimazione fatta sia
lecita:
dato che la [OH-] = 10-10 M deriva dalla dissociazione delle
molecole di H2O, la [H3O+] derivante dalla medesima
dissociazione sarà uguale, cioè pari a 10-10 M.
Questa concentrazione è trascurabile rispetto alla
concentrazione di [H3O+] derivante dall’acido (10-4 M)
Si calcoli il pH di una soluzione 5,0 · 10-8 M di HClO4
(acido forte: totalmente ionizzato)
HClO4 è un acido forte con Ka molto grande (possiamo considerarla
infinita) quindi in H2O si dissocia completamente:
HClO4
(aq)
+ H2O
(l)
→ ClO4-(aq) + H3O+(aq)
[H3O+] derivante dall’acido = [HClO4]= 5,0·10-8 M
+
−8
pH = −log10 [H 3O ] = −log10 [5,0 ⋅10 ] = +7,30
Impossibile:
la soluzione è basica?!
Tale concentrazione è paragonabile all’autodissociazione delle molecole
di acqua che, quindi, contribuirà al pH della soluzione.
2 H2O(l) ⇄ H3O+(aq) + OH-(aq)
5,0·10-8
Ciniziali)
Variazione di C(Δ)
+x
5,0·10-8+x
Cequilibrio)
----
+x
+x
Kw = [H3O+]·[OH-]
allora:
Kw = (5,0·10-8 + x)· x = 1,0 ·10-14
risolvendo l’equazione di secondo grado: x2+5,0·10-8x - 1,0 ·10-14=0
si ottiene:
x = 7,81· 10−8 M
la concentrazione totale di [H3O+] = 5,0·10-8+x = 1,281 · 10-7 M
pH = −log10[H3O+] = -log10[1,281 ·10−7] = 6,89
Si noti che il pH è acido come atteso.
In generale, solo quando gli ioni H3O+ derivanti da un acido forte sono
in concentrazione << 10-6 M occorre tenere conto del contributo della
dissociazione dell’acqua per il calcolo del pH.
Calcolo del pH di soluzioni molto diluite di acidi forti
Trattazione generale (trattamento sistematico)
sistematico)::
Indichiamo con HX il generico acido forte di concentrazione 10-8<Ca<10-6 mol/L
Essendo la concentrazione dell’acido estremamente bassa, non è più possibile
trascurare il contributo degli ioni H3O+ provenienti dalla dissociazione
dell’acqua. Il problema deve essere risolto impostando i bilanci di carica e di
massa relativi agli equilibri di dissociazione delle varie specie presenti in
soluzione. Teniamo presente che l’acido HX è un acido forte, quindi
completamente dissociato:
HX
(aq)
+ H2O
(l)
→ H3O+(aq) + X-(aq)
ed è presente l’equilibrio di dissociazione dell’acqua:
2 H2O(l) ⇄ H3O+(aq) + OH-(aq)
Le relazioni che legano le varie specie presenti in soluzione sono:
[X − ] = C a
a) Bilancio di massa sul X−
b) Bilancio di carica (la soluzione deve essere elettroneutra):
[H 3O + ] = [OH − ] + [ X − ]
c) Equilibrio dell’acqua
+
−
K w = [H 3O ] ⋅ [OH ]
Sostituendo [X-] = Ca nella (b) e ricavando [OH-] dalla (c), l’equazione (b) diventa:
Kw
[H 3O ] = Ca +
+
[H 3O ]
+
da cui risolvendo rispetto ad [H3O+] si ottiene:
+ 2
+
[H 3O ] − C a ⋅ [H 3O ] − K w = 0
Calcolo del pH: basi forti
Esercizio 1:
Si calcoli il pH di una soluzione acquosa 5,0 · 10-4 M
di NaOH. Risultato: 10,7
Esercizio 2:
Si calcoli il pH di una soluzione acquosa 5,0 · 10-4 M di
Ba(OH)2. Risultato: 11,0
Perchè se la
concentrazione
è la stessa ?
Entrambe sono totalmente dissociate in acqua:
1) NaOH (aq) → Na
2) Ba(OH)2
(aq)
+
(aq)
→ Ba
+ OH
++
(aq)
−
(aq)
+ 2 OH
−
(aq)
Tuttavia nel secondo caso la concentrazione
dell’OH− è doppia:
1) [OH − ] = [NaOH] = Na + = 5 ⋅10 −4 M
[
]
[
]
2) [OH − ] = 2 ⋅ [Ba(OH)2 ] = 2 ⋅ Ba + + = 2 ⋅ 5 ⋅10 − 4 M = 10 −3 M
1) pOH = −log[OH − ] = − log [5 ⋅10 −4 ] = 3,3
2) pOH = −log[OH − ] = − log [10 −3 ] = 3,0
1) pH = 14 − pOH = 14 − 3,3 = 10,7
2) pOH = 14 − pOH = 14 − 3,0 = 11,0
Calcolo del pH di soluzioni molto diluite di basi forti
trattamento sistematico
Indichiamo con MOH la generica base forte di concentrazione 10-8<Cb<10-6 mol/L
Essendo la concentrazione della base estremamente bassa, non è più possibile
trascurare il contributo degli ioni H3O+ provenienti dalla dissociazione
dell’acqua. Il problema deve essere risolto impostando i bilanci di carica e di
massa relativi agli equilibri di dissociazione delle varie specie presenti in
soluzione. Teniamo presente che la base MOH è un base forte, quindi
completamente dissociata ne catione M+ e anione OH−:
MOH
H2O
(aq)
→
M+(aq) + OH-(aq)
ed è presente l’equilibrio di dissociazione dell’acqua:
2 H2O(l) ⇄ H3O+(aq) + OH-(aq)
Le relazioni che legano le varie specie presenti in soluzione sono:
a) Bilancio di massa sul M+
[M + ] = C b
+
+
−
[H 3O ] + [M ] = [OH ]
b) Bilancio di carica
c) Equilibrio dell’acqua
+
−
K w = [H 3O ] ⋅ [OH ]
Sostituendo [M+] = Cb nella (b) e ricavando [H3O+] dalla (c), l’equazione (b) diventa:
Kw
−
Cb +
= [OH ]
−
[OH ]
da cui risolvendo rispetto ad [H3O+] si ottiene:
− 2
−
[OH ] − C b ⋅ [OH ] − K w = 0
Calcolo del pH di soluzioni di acidi forti e basi forti
trattamento sistematico
Concentrazioni (10-6-10-8M),
qui è necessario il trattamento
sistematico
Concentrazioni alte (≥ 10-6M), il
pH è calcolato da H3O+ e OHderivante dall’acido o dalla
base
Bassissime concentrazioni
(≤10-8M), il pH=7 H3O+,OHnon sono abbastanza per
cambiare il pH
Applicazione della legge di azione delle
masse agli equilibri acido-base
Per calcolare il pH di Acidi e basi deboli abbiamo bisogno di
introdurre rispettivamente le costanti di ionizzazione acida
(Ka) e la costante di ionizzazione basica (Kb)
La forza di un acido (o di una base) si “misura” con il valore della relativa
costante (termodinamica) del seguente equilibrio omogeneo in fase
liquida (acquosa):
HA + H2O ⇄ H3O+ + APer gli acidi forti la costante è >>1 : in altre parole sono
completamente ionizzati e la concentrazione di H3O+ e di Asono uguali alla concentrazione iniziale dell’acido
In questo caso non si parla più di equilibrio!! Ma di reazione
completamente spostata a destra.
Acidi e basi deboli
Per acidi deboli la costante è <1 : in altre parole sono
poco
ionizzati
e
in
soluzione
sono
presenti
contemporaneamente i prodotti (H3O+ e A-) e il reagente
(cioè l’acido indissociato sottoforma di molecola discreta)
tanto minore è il valore di Ka, tanto minore è la
frazione di molecole dissociate nei loro ioni
La costante Ka (è detta costante di dissociazione (o
ionizzazione) acida) (è una costante di un equilibrio omogeneo in
fase liquida, una KC):
Consideriamo l’acqua
un liquido puro #
come
HClO2(aq)
aq) + H2O(l) ⇄ ClO2-(aq)
aq) + H3O+(aq)
aq)
Ka =
a ClO − ⋅ a H O +
2
3
a H 2O ⋅ a HClO2
−
2
+
[ClO ] ⋅ [H 3O ]
=
[HClO 2 ]
# la sua attività è unitaria e stiamo, inoltre, assumendo che la costante di acidità
(secondo Brönsted-Lowry) numericamente coincida con quella di dissociazione…
#oppure si può dire che essendo la concentrazione dell’acqua pressoché costante
anche il rapporto KC/[H2O] sarà costante:
[ClO 2− ] ⋅ [H 3O + ]
KC
[ClO −2 ] ⋅ [H 3O + ]
KC =
⇒ Ka =
=
[H 2 O] ⋅ [HClO 2 ]
[H 2 O]
[HClO 2 ]
Spesso sono deboli gli acidi organici con il gruppo funzionale –COOH
pKa = −log10(Ka)
Conviene fare come il pH
più piccolo è il valore del pK più forte è l’acido (ovvero è meno debole)
La costante (di basicità) Kb
(è una costante di un equilibrio omogeneo in fase liquida, una KC):
Consideriamo l’acqua come
un liquido puro #
NH3(aq
aq)) + H2O(
O(ll) ⇄ NH4+(aq
aq)) + OH-(aq
aq))
Kb =
a NH + ⋅ a OH −
4
a H 2O ⋅ a NH3
+
4
−
[NH ] ⋅ [OH ]
=
[NH 3 ]
oppure
+
4
−
+
4
−
KC
[NH ] ⋅ [OH ]
[NH ] ⋅ [OH ]
KC =
⇒ Kb =
=
[H 2 O] ⋅ [NH 3 ]
[H 2 O]
[NH 3 ]
pKb = −log10(Kb)
Spesso sono deboli le basi che derivano dall’ammoniaca per sostituzione di –H
con gruppi organici
Calcolo del pH per un acido debole (Ka < 1) monovalente
(monoprotico) di concentrazione (iniziale)
Ca (ignoriamo la
dissociazione dell’acqua ed assumiamo che gli ioni H3O+ derivino solamente dalla
dissociazione dell’acido debole; tale assunzione è quasi sempre verificata, ovvero
è verificata quando il valore del pH viene inferiore o uguale a 6)
Indichiamo con HA il generico acido debole:
(i)
(eq)
HA(aq)) + H2O(
HA(aq
O(ll) ⇄ A-(aq
aq)) + H3O+(aq
aq))
~0
Ca
--(Ca – x)
x
x
[A − ] [H 3O + ]
Ka =
[HA]
Ka =
x = [A − ] = [H 3O + ]
x2
(c a − x)
Generalmente dovremmo risolvere un’equazione di secondo grado!
Se dovessimo tener conto dell’autodissociazione dell’acqua si può dimostrare che
dovremmo addirittura risolvere un’equazione di terzo grado rispetto ad H3O+
Vediamo se si possono fare delle approssimazioni……..
….riscrivo la costante Ka così:
+ 2
[H 3O ]
Ka =
[HA]
da cui
+
[H 3O ] = K a ⋅ [HA]
Se α < 0,05, cioè se si dissociano (ionizzano) meno di 5 mol di HA su 100 mol,
posso effettuare questa approssimazione:
[HA] ≅ C a
+
[ H 3O ] = K a ⋅ C a
Concentrazione iniziale
Perchè posso effettuare questa approssimazione? Basta ricordare che per un elettrolita
debole uno-unovalente vale la legge di diluizione di Ostwald (vedi lezione 17):
α2
K=
⋅ C0
1− α
Nel nostro caso se
⇒
C0 1 − α
= 2
K
α
Ca
> 380 ⇒ α < 0,05
Ka
Invece quando
Ca
≤ 380
Ka
⇒ α ≥ 0,05
+
[HA] = C a − [H 3O ]
+
+
[H 3O ] = K a ⋅ (C a − [H 3O ])
Dobbiamo risolvere l’equazione di secondo grado:
+ 2
+
[ H 3O ] + K a ⋅ [ H 3O ] − K a ⋅ C a = 0
…. ricordando che …
ax + bx + c = 0
2
− b ± b − 4ac
x=
2a
2
− K a + K a + 4 Ca K a
[ H 3O ] =
2
2
+
Calcolo del pH per un Base debole monovalente (Kb < 1) di
concentrazione (iniziale) Cb (ignoriamo la dissociazione dell’acqua ed
assumiamo che gli ioni OH− derivino solamente dalla dissociazione della base
debole );vale un ragionamento analogo a quello degli acidi deboli.
Indichiamo con B la generica base debole:
B(aq
B(
aq)) + H2O(
O(ll) ⇄ BH+(aq
aq)) + OH-(aq
aq))
(i)
Cb
--~0
(eq) (Cb – x)
x
x
2
x
[BH ] [OH ] x = [BH + ] = [OH − ] K =
Kb =
b
(C b − x)
[B]
Cb
Se
> 380 ⇒ α < 0,05
Cb − x ≅ Cb
Kb
x2
[OH − ]2
Kb =
Kb ≅
Cb
Cb
+
−
−
[OH ] = K b ⋅ C b
Se
Cb
≤ 380
Kb
⇒ α ≥ 0,05
−
[B] = C b − [OH ]
[BH + ] [OH − ]
[OH − ]2
Kb =
=
−
C b − [OH ] C b − [OH − ]
Dobbiamo risolvere l’equazione di secondo grado:
− 2
−
[OH ] + K b ⋅ [OH ] − K b ⋅ C b = 0
Chimica
(a.a. 2011/2012, 6CFU)
Equilibri ionici in soluzione acquosa (II parte):
Idrolisi delle soluzioni saline
Calcolo del pH nelle idrolisi
Acidi e basi polifunzionali
Le soluzioni tampone
IDROLISI DEI SALI
Molti sali contengono un anione o un catione che possono
reagire con acqua rendendo
le loro soluzioni ACIDE o BASICHE
Molti sali reagiscono con l’acqua alterando il suo
rapporto molare tra [H3O+] e [OH-]
La soluzione assume un pH maggiore oppure minore di 7
(generalmente è un effetto causato da uno degli ioni del sale)
Come prevedere?
Basicità e acidità di cationi ed anioni
−
Perché?
2
Vediamo di
razionalizzare questa
tabella?
*
* Cationi di metalli piccoli e con alta carica legano fortemente
molecole d’acqua, indeboliscono il legame O-H con effetti acidi
Soluzioni di Sali in acqua
Un sale deriva dalla reazione di neutralizzazione di un acido e
di una base in soluzione acquosa.
In soluzione acquosa i sali sono dissociati negli ioni costituenti:
H2O
→ Na+ (aq) + Cl- (aq)
H2O
NH4Cl(s) →
NH4+ (aq) + Cl- (aq)
H2O
CH3COONa(s) →
CH3COO- (aq) + Na+ (aq)
2O CH COO- (aq) + NH + (aq)
CH3COONH4(s) H→
3
4
NaCl(s)
Abbiamo visto che nella teoria di Brønsted e Lowry anche gli
ioni possono comportarsi da acidi o da basi, in particolare se
sono gli acidi o le basi coniugati di basi o acidi deboli,
rispettivamente. Ioni che invece sono i coniugati di acidi o basi
forti invece non hanno proprietà basiche o acide.
Se abbiamo una soluzione di NaCl, poiché gli ioni costituenti
sono i coniugati di un acido forte (HCl) e di una base forte
(NaOH), Na+ e Cl- non hanno alcuna tendenza ad accettare o
donare protoni all’acqua
Na+ (aq) + H2O
Cl- (aq) + H2O
/
/
→
→
nessuna reazione
nessuna reazione
La soluzione risulterà quindi neutra.
Consideriamo ora una soluzione ottenuta sciogliendo NH4Cl in
acqua
H O
2
NH4Cl (s) →
NH4+ (aq) + Cl-(aq)
Mentre lo ione Cl- è stabile in acqua, lo ione NH4+ è l’acido
coniugato della base debole NH3 è quindi in grado di cedere un
protone all’acqua secondo la reazione:
NH4+ (aq) + H2O(l)
NH3 (aq) + H3O+ (aq)
NH4+ (aq) + H2O(l)
NH3 (aq) + H3O+ (aq)
La soluzione risulterà dunque acida.
La reazione tra NH4+ e H2O fondamentalmente non è diversa
dalle altre reazioni acido-base. Tuttavia una reazione tra uno
ione e l’acqua viene detta REAZIONE DI IDROLISI. Si dice
allora che lo ione ammonio si idrolizza (a differenza dello ione
cloruro).
Quando sciogliamo in acqua del cianuro di sodio, NaCN:
NaCN (s)
H2O
Na+ (aq) + CN- (aq)
in questo caso lo ione Na+ è stabile, mentre lo ione CN- è la
base coniugata dell’acido cianidrico HCN, è quindi in grado di
accettare un protone dall’acqua secondo la reazione:
CN- (aq) + H2O (l)
HCN (aq) + OH- (aq)
la soluzione risulta dunque basica. Lo ione cianuro si idrolizza.
Costante di IDROLISI (BASICA
BASICA))
Prendiamo ad esempio il nitrito di sodio NaNO2 che si dissocia completamente il
acqua a dare il catione Na+ (acido debolissimo coniugato della base fortissima
NaOH) e l’anione NO2- (base debole coniugata dell’acido debole HNO2):
NaNO2(s) → Na+(aq
aq)) + NO2-(aq
aq))
NO2- è la base coniugata di HNO2, e quest’ultimo è un acido debole governato
dall’equilibrio:
−
+
+
HNO2(aq)
aq) + H2O(
O(ll) ⇄ NO2 (aq
aq)) + H3O (aq
aq))
2
3
a
IDROLISI BASICA:
2
[NO ] [H O ]
K =
[HNO ]
NO2-(aq
aq)) + H2O(
O(ll) ⇄ HNO2(aq
aq)) + OH-(aq
aq))
[HNO 2 ] [OH − ]
costante d' idrolisi = K i = K b =
−
[NO 2 ]
Si dimostra che la costante di idrolisi è una costante basica Kb che è uguale:
KW
Kb =
Ka
Costante di IDROLISI (ACICA
ACICA))
Prendiamo ad esempio il cloruro di ammonio NH4Cl che si dissocia completamente in
acqua a dare l’anione Cl- (base debolissima coniugato della acido fortissimo HCl) e
il catione NH4+ (acido debole coniugato della base debole NH3):
NH4Cl(
Cl(ss) → NH4+(aq
aq)) + Cl-(aq
aq))
NH4+ è l’acido coniugato di NH3, e quest’ultimo è una base debole governata
dall’equilibrio:
+
−
4
NH3(aq
aq)) + H2O(
O(ll) ⇄ NH4+(aq
aq)) + OH-(aq
aq))
b
3
IDROLISI ACIDA
ACIDA::
[NH ] [OH ]
K =
[NH ]
NH4+(aq
aq)) + H2O(
O(ll) ⇄ NH3(aq
aq)) + H3O+(aq
aq))
+
[NH 3 ] [H 3O ]
costante d' idrolisi = K i = K a =
+
[NH 4 ]
Si dimostra che la costante di idrolisi è una costante acida Ka che è uguale:
KW
Ka =
Kb
KW
Dimostrazione di K b =
Ka
ovvero K a ⋅ K b = K W
In tutti i casi,
casi, per una coppia acidoacido-base coniugati si ha:
Ka ⋅ Kb = KW
Per esempio, per la coppia NH4+/NH3:
Kb =
+
4
−
[NH ] [OH ]
[NH 3 ]
[NH 3 ] [H 3O + ]
costante d' idrolisi = K i = K a =
[NH +4 ]
Se moltiplico e divido Kb per la concentrazione di [H3O+]
[NH 4+ ] [OH − ] [H 3O + ] K w
Kb =
⋅
=
+
[NH 3 ]
[H 3O ] K a
KaKb = Kw
Oppure se moltiplico e divido Ka per la concentrazione di [OH-]
[NH 3 ] [H 3O + ] [OH − ] K w
Ka =
⋅
=
+
−
[NH 4 ]
[OH ] K b
KaKb = Kw
Inoltre
KW
Kb =
Ka
ovvero
Ka ⋅ Kb = KW
tale relazione mette in evidenza che la base
coniugata di un acido debole (o, viceversa,
l’acido coniugato di una base debole) è debole e
che il coniugato di un forte è debolissimo.
Calcolo del pH nelle idrolisi di sali basici (IDROLISI BASICA):
SALE BASICO derivante da ACIDO DEBOLE e BASE FORTE
Esempio l’acetato di sodio (CH3COONa) di concentrazione iniziale Cs
CH3COONa (acetato di sodio) → CH3COO- + Na+
(l’acetato di sodio è come se provenisse dalla reazione di NaOH e CH3COOH)
(i)
(eq)
CH3COO- (aq) + H2O(l)
CH3COOH(aq) + OH- (aq)
Cs
Cs-x
--x
~0
x
x = [OH-] = [CH3COOH]
−
K
[CH 3COOH] [OH ]
Ki = Kb = W =
Ka
[CH 3COO − ]
quando
Cs
> 380 ⇒ α < 0,05
Kb
CS − x ≅ CS
[OH − ]2
Kb =
CS
2
x
Kb =
(CS − x)
Cioè meno del 5% di CH3COO- si idrolizza
−
[OH ] = K b ⋅ Cs
CS
≤ 380
se
Kb
⇒ α ≥ 0,05
Cioè più del 5% di CH3COO- si idrolizza
−
− 2
[CH
COOH]
[OH
]
[OH
]
3
−
−
=
[CH 3COO ] = C s − [OH ] K b =
−
CS − [OH ]
CS − [OH − ]
Dobbiamo risolvere l’equazione di secondo grado:
− 2
−
[OH ] + K b ⋅ [OH ] − K b ⋅ CS = 0
−Kb + K + 4CS Kb
[OH ] =
2
−
Ricorda SEMPRE che
2
b
KW
Kb =
Ka
Calcolo del pH nelle idrolisi di sali acidi (IDROLISI ACIDA):
SALE ACIDO derivante da ACIDO FORTE e BASE DEBOLE
Esempio il cloruro di ammonio (NH4Cl) di concentrazione iniziale Cs
NH4Cl (cloruro di ammonio) → NH4+ + Cl(il cloruro di ammonio è come se provenisse dalla reazione di HCl e NH3)
(i)
(eq)
+
NH4+(aq)
aq) + H2O(l) ⇄ NH3 (aq) + H3O (aq)
aq)
CS
--~0
x
x
CS-x
x = [NH3] = [H3O+]
+
K W [NH 3 ] [H 3O ]
Ki = Ka =
=
+
Kb
[NH 4 ]
quando
Cs
> 380 ⇒ α < 0,05
Ka
CS − x ≅ CS
[H 3O + ]2
Ka =
CS
2
x
Ka =
(CS − x)
Cioè meno del 5% di NH4+ si idrolizza
+
[H 3O ] = K a ⋅ CS
se
CS
≤ 380
Ka
⇒ α ≥ 0,05
+
+
[NH 4 ] = Cs − [H 3O ]
Cioè più del 5% di NH4+ si idrolizza
[NH 3 ] [H 3O + ] [H 3O + ]2
[H 3O + ]2
Ka =
=
=
+
+
+
[NH 4 ]
[NH 4 ] Cs − [H 3O ]
Dobbiamo risolvere l’equazione di secondo grado:
+
+
[H 3O ] + K a ⋅ [H 3O ] − K a ⋅ CS = 0
2
− Ka + Ka + 4 CS Ka
[H3O ] =
2
KW
Ka =
SEMPRE che
Kb
2
+
ricorda
Sali di acidi deboli e basi deboli
Ad esempio
NH4CN → NH4+ + CN(è come se derivasse da NH3 e HCN)
CH3COONH4 → CH3COO- + NH4+
(è come se derivasse da NH3 e CH3COOH)
NH4F → NH4+ + F(è come se derivasse da NH3 e HF)
Sia il catione che l’anione hanno la tendenza ad idrolizzarsi, ma l’effetto
che il sale ha sul pH dipende dalla capacità del catione di generare H+
(ovvero H3O+) rispetto a quella dell’anione di generare OH- (e viceversa )
Considerare caso per caso
1° caso
NH4CN → NH4+ + CN-
Cianuro di ammonio
(è come se derivasse da NH3 e HCN)
[1]
NH4+ + H2O →
K b,NH3 = 1,8 ⋅10−5
[2]
KW
10 −14
−10
K idrolisi,1 = K a =
=
=
5,55
⋅
10
K b,NH3 1,8 ⋅10 −5
CN- + H2O →
K a,HCN = 6,16 ⋅10
−10
NH3 + H3O+
HCN + OH-
KW
1,0 ⋅10 −14
−5
K idrolisi,2 = K b =
=
=
1,62
⋅
10
K a, HCN 6,16 ⋅10 −10
Poiché
Kidrolisi
idrolisi,2
,2 >>> Kidrolisi
idrolisi,1
,1
SOLUZIONE BASICA
pH>7
2° caso
Acetato di ammonio
CH3COONH4 → NH4+ + CH3COO(è come se derivasse da NH3 e CH3COOH)
[1]
NH4+ + H2O →
K b,NH3 = 1,8 ⋅10−5
[2]
NH3 + H3O+
KW
10 −14
−10
K idrolisi,1 = K a =
=
=
5,55
⋅
10
K b,NH3 1,8 ⋅10 −5
CH3COO- + H2O →
K a,CH 3COOH = 1,8 ⋅10−5
CH3COOH + OH-
K idrolisi,2 = K b =
Poiché
KW
K a,CH 3COOH
10 −14
−10
=
=
5,55
⋅
10
1,8 ⋅10 −5
Kidrolisi
idrolisi,2
,2 = Kidrolisi
idrolisi,1
,1
SOLUZIONE NEUTRA
pH=7
3° caso
Fluoruro di ammonio
NH4F → NH4+ + F(è come se derivasse da NH3 e HF)
[1]
NH4+ + H2O →
K b,NH3 = 1,8 ⋅10−5
[2]
KW
10 −14
−10
K idrolisi,1 = K a =
=
=
5,55
⋅
10
K b,NH3 1,8 ⋅10 −5
F- + H2O →
K a,HF = 6,16 ⋅10
−10
NH3 + H3O+
HF + OH-
KW
1,0 ⋅10 −14
−11
K idrolisi,2 = K b =
=
=
1,58
⋅
10
K a, HF 6,31 ⋅10 − 4
Poiché
Kidrolisi
idrolisi,2
,2 <<< Kidrolisi
idrolisi,1
,1
SOLUZIONE ACIDA
pH<7
pH di Soluzioni di Sali
In termini generali:
Sali derivanti di ACIDI FORTI E BASI FORTI (per esempio:
NaCl, KCl, KNO3, BaI2, NaClO4, etc.) NON SI IDROLIZZANO
IDROLIZZANO. La
soluzione ha pH=
pH=7
7 (soluzioni
soluzioni neutre
neutre)
Sali derivanti di ACIDI DEBOLI E BASI FORTI (per esempio:
CH3COONa, KNO2, NaClO2, etc.) SI IDROLIZZANO
IDROLIZZANO. Il pH>
pH>7
7
(L’anione si comporta da base, soluzioni basiche
basiche)
Sali di derivanti ACIDI FORTI E BASI DEBOLI (NH4Cl, NH4NO3,
NH4Br, NH4ClO4, etc.) SI IDROLIZZANO
IDROLIZZANO. Il pH<
pH<7
7 (Il catione si
comporta da acido, soluzioni acide
acide)
Sali di derivanti ACIDI DEBOLI E BASI DEBOLI (NH4CN,
NH4NO2, CH3COONH4, etc.) SI IDROLIZZANO
IDROLIZZANO. Il pH dipende
dalla forza relativa dell’acido e della base (I cationi si
comportano da acidi e gli anioni da basi).
pH di Soluzioni di Sali
Riassumendo
*
*
*
* Per il livello del nostro corso solo per questi
casi bisogna essere in grado di calcolare il pH.
Acidi e basi poliprotici
Diciamo acido poliprotico un composto atto a cedere più di un protone.
Molti acidi comuni hanno struttura poliprotica: tra di essi l'acido
solforico, H2S04, l' acido carbonico, H2C03, capaci entrambi di cedere
due protoni, e l'acido fosforico, H3P04, che può cederne tre. Nei sistemi
biologici gli acidi poliprotici assolvono un ruolo decisivo; molti enzimi si
possono considerare acidi poliprotici che espletano le funzioni vitali
cedendo un protone dopo l'altro. Una base poliprotica è una specie che è
in grado di accettare più di un protone; tra gli esempi ricordiamo gli
anioni CO32- e SO32-, capaci di accettare due protoni, e lo ione PO43-,
capace di accettarne tre.
La differenza principale tra un acido poliprotico e uno monoprotico è che il
primo cede i suoi protoni in successione. Ad esempio, l'acido carbonico può
cedere un protone formando HCO3-, e successivamente questo ione può
cedere il protone rimanente dando CO32-. Nel valutare il pH della soluzione
di un acido poliprotico o di un suo sale occorre sapere quando e come
tener conto di queste serie di processi di deprotonazione.
Acidi e basi poliprotici
Specie che cedono o accettano più di un protone sono
dette poliprotiche
Un acido è detto monoprotico se può liberare un solo protone
e poliprotico se può liberarne più di uno (diprotico, triprotico, ecc.)
Una base é detta monoprotica se può fissare (accettare) un solo protone
e poliprotica se può fissarne (accettarne) più di uno (diprotica,
triprotica, ecc.)
Esempi di Acidi Poliprotici
Gli acidi poliprotici danno luogo a tanti equilibri diversi con l'acqua quanti sono
i protoni che possono cedere. Ad esempio, H3PO4 dà luogo agli equilibri
seguenti:
H3PO4(aq) + H2O(l) ⇄ H2PO4-(aq) + H3O+(aq)
Ka1 = 7,1×10-3
H2PO4-(aq) + H2O(l) ⇄ HPO42-(aq) + H3O+(aq)
Ka2 = 6,2×10-8
HPO4-(aq) + H2O(l) ⇄ PO43-(aq) + H3O+(aq)
Ka3 = 4,4×10-13
H2CO3(aq) + H2O(l) ⇄ HCO3-(aq) + H3O+(aq)
Ka1 = 4,4×10-7
HCO3-(aq) + H2O(l) ⇄ CO32-(aq) + H3O+(aq)
Ka2 = 4,7×10-11
H2SO4(aq) + H2O(l) ⇄ HSO4-(aq) + H3O+(aq)
Ka1 = ~102 (forte)
HSO4-(aq) + H2O(l) ⇄ SO42-(aq) + H3O+(aq)
Ka2 = 1,05×10-2
Regola generale: i successivi stadi sono caratterizzati da costanti di
equilibrio via via decrescenti.
La forza di un acido poliprotico diminuisce di un fattore 104÷105, o superiore,
in ogni dissociazione successiva.
Calcolo del pH in Soluzioni di Acidi Poliprotici
•
Per esempio, nel caso di un acido diprotico, in soluzione acquosa si instaurano i
seguenti equilibri:
[
H O ]⋅ [HA ]
=
+
H2A + H2O
HA− + H2O
H3O+ + HA-
H3O+ + A2−
• Si verifica sempre che: Ka1 > Ka2
• Spesso: Ka1 >> Ka2
K a1
3
-
[H 2 A]
[H 3O + ] ⋅ [A 22−− ]
K a2 =
[HA - ]
Calcolo del pH in Soluzioni di Acidi Poliprotici
• Se Ka1/Ka2 > 103
– Si può assumere con buona approssimazione che H3O+ sia dovuto
esclusivamente al primo equilibrio di dissociazione
• Se Ca/Ka1 > 380
– È possibile utilizzare l’espressione approssimata per il calcolo di
[H3O+] di un acido debole
[H 3O + ] = K a1 ⋅ C H 2 A
Altrimenti si utilizza la soluzione dell’equazione quadratica:
[H O ] =
+
3
− K a1 + K a1 + 4 ⋅ K a1 ⋅ C H 2 A
2
2
Che è comunque
un’approssimazione, perché si
trascura il contributo
dell’autodissociazione dell’acqua
In generale: il pH di un acido poliprotico, le cui deprotonazioni sono tutte
deboli, si calcola considerando esclusivamente il primo equilibrio di
deprotonazione assumendo che le deprotonazioni successive siano prive di
importanza.
Determinazione delle Concentrazioni Ioniche di un
Acido diprotico. Un caso particolare :
H2SO4 (l’acido solforico)
L’acido solforico differisce dalla maggior parte degli acidi poliprotici
perché nella sua prima ionizzazione è un acido forte e nella seconda è
debole. Nel primo stadio la ionizzazione è completa!!!
Infatti, l’acido solforico è l'unico acido poliprotico comune che subisca in modo
completo la prima deprotonazione; la seconda aggiunge poco alla molarità di H30+,
il pH complessivo sarà appena un po’ minore di quello dovuto alla sola prima
deprotonazione. Ad esempio, in H2S04(aq) 0,010 M la prima deprotonazione
H2SO4(aq) + H2O(l) →HSO4-(aq) + H3O+(aq)
Ne discende una molarità di H30+ uguale a quella iniziale dell'acido, 0,010 mol/L,
valore che corrisponde a pH = 2,0. Tuttavia anche la base coniugata, HSO4-,
contribuisce con una parte dei propri protoni, per cui è necessario tener conto del
secondo equilibrio di trasferimenuo protonico:
HSO4-(aq) + H2O(l) ⇄ SO42-(aq) + H3O+(aq)
Ka2 = 1,05×10-2
In definitiva, per calcolare il pH della soluzione di acido solforico costruiremo
una tabella di equilibrio nella quale le concentrazioni iniziali siano quelle dovute
alla prima deprotonazione: [HSO4-] = 0,010 mol·L-1, [H30+] = 0,010 mol·L-1 e
[SO42-]=0 mol·L-1.
H3O+ + SO42-
HSO4- + H2O
Concentrazione iniziale
Variazioni
Concentrazione
all’equilibrio
0,010
-x
0,010-x
+ 0,010
+x
0,010+x
~0
+x
+x
(
[H 3O + ] ⋅ [SO 24− ]
0,010 + x ) ⋅ x
−2
K a2 =
= 1,05 ⋅10 =
−
[HSO 4 ]
0,010 − x
si ottiene l’equazione di secondo grado:
x 2 + 2,05 ⋅10 −2 x − 1,05 ⋅10 −4 = 0
x = 0,00424
[H 3O + ] = 0,010 + x = 0,010 + 0,00424 = 0,01424
la cui radice positiva:
pH = −log 10 [H 3O + ] = −log 10[0,01424] ≅ +1,85
In generale per l’acido solforico:
Quando la sua concentrazione è compresa fra 6·10–4 M e 0,15 M, per il
calcolo del pH si procede come visto poco anzi.
Invece l’acido solforico può essere considerato completamente dissociato in
entrambi gli stadi se la sua concentrazione è minore di 6·10–4 M:
H2SO4 (aq) + 2 H2O(l) → SO42-(aq) + 2 H3O+(aq)
[H 3O + ] ≡ 2 ⋅ C a = 2 ⋅ [H 2SO 4 ]
pH = −log 10[2 ⋅ C a ]
Se l’acido solforico è in concentrazione maggiore di 0,15 M, il secondo
stadio di dissociazione è completamente spostato a sinistra e l’acido si
comporta da monoprotico secondo la reazione:
H2SO4(aq) + H2O(l) → HSO4−(aq) + H3O+(aq)
[H 3O + ] ≡ C a = [H 2SO 4 ]
pH = −log 10[C a ]
Il pH delle Sostanze anfiprotiche
La base coniugata di un acido poliprotico è necessariamente anfiprotica, potendo agire sia
da acido sia da base; essa può infatti cedere l'atomo di idrogeno acido rimanente oppure
accettare un atomo di idrogeno ricostituendo l'acido originale. Per fare un esempio, lo ione
idrogenosolfuro, HS−, agisce in acqua sia da acido sia da base:
HS− + H2O
H3O+ + S2-
[H 3O + ] ⋅ [S2− ]
−19
K a2 =
=
1
,
0
⋅
10
[HS- ]
HS− + H2O
H2S + OH−
K w [H 2S] ⋅ [OH − ] 1,0 ⋅10 −14
−7
K idrolisi = K b =
=
=
≅
1,124
⋅
10
K a1
[HS − ]
8,9 ⋅10 −8
Sorge l'interrogativo se la soluzione di un sale di HS-, poniamo NaHS, sia acida grazie al
carattere acido di HS-, oppure basica, a causa del carattere basico dello stesso ione.
Si dimostra che adittando alcuni criteri logici e svolgendo un po' di algebra, risulta che il pH
della soluzione è
+
3
a1
a2
10
a1
a2
indipendentemente dalla concentrazione del sale.*
[H O ] = K ⋅ K
*A
patto che
Csale >> K W /K a2
1
⇒ pH = − log
2
e Csale >> K a1
Comunque non vedremo esercizi sulle sostanze anfiprotiche ……
Ma è bene che sappiate ….
(K
⋅K
)
.. che quando il bicarbonato di sodio (NaHCO3) è sciolto in acqua,
produce una soluzione lievemente basica. Per esempio una soluzione di
50 g in un litro di acqua a 25 °C ha il pH di circa 8,34:
NaHCO3 → Na++HCO3-
g
50
g
50
g
=
=
≅ 0,595 M
g
L PM NaHCO3 L 84,0066
L
mol
Per l’acido carbonico (H2CO3) da cui deriva il bicarbonato:
Csale = [HCO 3− ] = 50
Csale >> K W /K a2
e Csale >> K a1
K a1 = 4,4 ⋅10−7
K a2 = 4,7 ⋅10−11
[H 3O + ] = K a1 ⋅ K a2 = 2,068 ⋅10 −17 = 4,55 ⋅10 −9 M
(
)
pH = −log 10 4,55 ⋅10 −9 = 8,34
Quando in una soluzione sono
presenti sia l’acido debole (HA
HA))
che la sua base coniugata (A-) …
che succede? Come si calcola il
pH?
HA(aq) + H2O(l) ⇄ A-(aq) + H3O+(aq)
Ca
CS
?
Quando in una soluzione sono presenti sia l’acido
debole che la sua base coniugata … che succede?
Come si calcola il pH?
Si ha una Soluzione tampone
Un soluzione tampone è una soluzione che varia in maniera
trascurabile il proprio pH in seguito all’aggiunta di quantità
moderate di un acido o di una base forte.
Se ad un litro di acqua pura vengono aggiunte 0,01 moli di HCl
il pH varia da 7 a 2 (pH=-log(0,01) =2,0), cioè di 5 unità.
L’aggiunta della stessa quantità di HCl ad un litro di soluzione
tampone può far variare il pH di circa 0,1 unità.
Per questo motivo le soluzioni tampone
anche a livello biologico. Per esempio il
tampone ed ha un pH di circa 7,4
trasportatore di ossigeno risulterebbe
valore dovesse variare.
sono molto importanti,
sangue è una soluzione
e la sua funzione di
compromessa se tale
I tamponi possono essere costituiti da:
- un acido debole e la sua base coniugata (es. HCN/CN-)
- una base debole e il sua acido coniugato (es. NH3/NH4+)
Una soluzione tampone contiene quindi una coppia acidobase coniugata cioè un acido e la sua base coniugata in
equilibrio fra di loro. All’aggiunta di un acido o di una
base forte l’equilibrio si sposta dalla parte della base o
dell’acido deboli che costituiscono il tampone “assorbendo”
così l’eccesso di ioni H+ (ovvero H3O+) o di OH-.
Consideriamo ad esempio il tampone costituito da HClO e ClO-
Quando in una soluzione sono presenti sia
l’acido debole che la sua base coniugata …
Per esempio:
HClO(aq)) + H2O(
HClO(aq
O(ll) ⇄ ClO-(aq
aq)) + H3O+(aq
aq))
(i) Ca
CS
--(eq) Ca-x
CS+x
x
[ClO − ] [H 3O + ] (Cs + x)x
Ka =
=
[HClO]
(Ca − x)
[H 3O + ] = x
quando Ca e Cs sono paragonabili (e non molto piccole), cioè 0,1 < (Ca /Cs) < 10
Se si calcola x si vede che x << Ca e x << Cs
na
(Cs + x)x Cs [H 3O + ]
C
n
Ka =
≅
⇒ [H 3O + ] ≅ K a a = K a V = K a a
nS
(Ca − x)
Ca
CS
nS
V
na
[H 3O ] = K a
ns
+
Le soluzioni tampone
Qualora, in una soluzione acquosa, siano presenti un acido
debole ed la sua base coniugata (ad esempio: CH3COOH e
CH3COO- oppure NH4+ e NH3, etc.) si ha una SOLUZIONE
TAMPONE quando il rapporto fra le concentrazioni
stechiometriche dell’acido e della base è compreso tra 0,1 e 10
Le soluzioni tampone hanno proprietà chimiche peculiari:
• Il pH non varia al variare della
comunque non deve essere eccessiva);
diluizione
(che
• Il pH tende a rimanere costante per moderate (non
eccessive) aggiunte di acidi e basi forti.
Tampone: l’acido acetico (CH3COOH) e il sale
acetato (CH3COO-)
Cacido=Ca
Csale=Cs
CH3COOH(aq) + H2O(l) ⇄ CH3COO- (aq) + H3O+ (aq)
[CH 3COO − ] [H 3O + ]
Ka =
[CH 3COOH]
Esplicitando [H3O+]:
[CH 3COOH]
[H 3O ] = K a
−
[CH 3COO ]
+
−
e quindi:
quando
[CH 3COO ]
pH = pK a + log10
[CH 3COOH]
Ca
0,1 <
< 10
Cs
CS
pH = pK a + log 10
Ca
Oppure
Nota come equazione di
Henderson e Hasselbach
nS
pH = pK a + log 10
na
Se le concentrazioni delle due specie CH3COOH e
CH3COO- sono uguali:
pH = pKa
il tampone si dice perfetto
Tampone:
ad esempio la coppia coniugata NH3/NH4+
NH3(aq)
aq) + H2O(
O(ll) ⇄ NH4+(aq)
aq) + OH-(aq)
aq)
(i) Cb
(eq) Cb-x
Cs
Cs+x
x
Se 0,1 < Cs/Cb < 10, con un ragionamento analogo al precedente si
nb
ottiene:
nb
Cb −x
Cb
V
[OH ] = K b ⋅
≅ Kb ⋅
= Kb ⋅
= Kb ⋅
ns
ns
Cs + x
Cs
nb
V
−
[OH ] = K b
ns
nb
ns
−
pOH = −log10 OH = −log10 K b ⋅
= pK b + log10
ns
nb
pH = 14 − pOH
−
[
]
Sei metodi di preparazione di un tampone
Un tampone è sempre costituito da un acido debole HA e la sua
base coniugata A- oppure da una base debole B e il suo acido
coniugato B+. In pratica può essere preparato in vari modi:
Come opera un tampone
Esempio di Soluzioni Tampone: il tampone acido acetico-acetato
Lo ione acetato, la base coniugata dell’acido acetico, assorbe i protoni quando
viene aggiunto un acido forte. In tal modo il rapporto [base coniugata]/[acido] è
approssimativamente costante, per cui la variazione di pH è minima.
Analogamente, l’acido acetico agisce da donatore di protoni quando viene aggiunta
una base forte, mantenendo il rapporto [base coniugata]/[acido]
approssimativamente costante e minimizzando la variazione di pH
Capacità Tampone
e Intervallo di Tamponamento
CAPACITA’ TAMPONE = Quantità di acido o base che il
tampone è in grado di neutralizzare senza che il suo pH
vari apprezzabilmente
E’ MASSIMA QUANTO LE CONCENTRAZIONI DI
ACIDO DEBOLE E BASE CONIUGATA SONO ALTE E
APPROSSIMATIVAMENTE UGUALI TRA LORO
INTERVALLO DI TAMPONAMENTO = Intervallo di pH
entro il quale un tampone neutralizza efficacemente gli
acidi e le basi aggiunte mantenendo il pH circa costante
È PARI A CIRCA 2 UNITA’ DI pH CENTRATE
INTORNO AL VALORE DEL pKa DELL’ACIDO DEBOLE
O DEL pKb DELLA BASE DEBOLE
Calcolo della variazione di pH di Soluzioni Tampone dopo
aggiunta di piccole quantità di acido o base forti
1. Si assume che la reazione di neutralizzazione proceda a completezza
e si determinano le nuove concentrazioni stechiometriche
2. Si usano le concentrazioni determinate per ricavare [H3O+] ed il pH
Lo schema può essere applicato anche alla coppia acido-base
BH+/B, dove B è la base e BH+ è l’acido.
Chimica
(a.a. 2011/2012, 6CFU)
Equilibri ionici in soluzione acquosa (III parte):
Esercitazione sul pH: acidi e basi forti, acidi deboli
monoprotici e basi deboli monovalenti, acidi deboli
poliprotici, idrolisi e soluzioni tampone.
Esercizi riassuntivi e integrativi
Esercitazione
Dal libro Nobile-Mastrorilli (Capitolo 15), oltre a studiare
gli esercizi svolti, dovete essere in grado di svolgere i
seguenti problemi:
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24 alle pag.538-541
Inoltre studiare le dispense tratte dal libro
Stechiometria per la chimica generale
di Paola Michelin Lausarot e Gian Angelo Vaglio:
Cap 13,14 e 16 e svolgere i relativi esercizi.
Leggere soltanto il cap. 15
Infine svolgere gli esercizi integrativi riportati
alla fine di questa lezione.
Acidi e basi forti
Un’industria scarica 30 litri/min di una soluzione acquosa di acido
cloridrico (HCl) a pH=2. Quanto ossido di magnesio (MgO) serve
per neutralizzare la soluzione scaricata in un’ora di lavorazione?
Svolgimento:
Tipologia di esercizio:
In un’ora di lavorazione:
1h=60 min
L
⋅ 60 min = 180 L
Vsoluzione = 30
min
acido cloridrico (HCl) elettrolita forte:
HCl(aq) + H2O(l) → H3O+(aq) + Cl-(aq)
[HCl] = [H 3O + ] = 10− pH = 10−2 M
Reazione di neutralizzare (reazione spostata a destra ha un K=1/Kw=10+14)
H3O+(aq
aq)) + OH (aq
aq)) → 2 H2O(l)
L’ossido di magnesio (MgO) fornisce l’OH−
MgO(s) + H2O(l)→ Mg(OH)2 → Mg2+(aq) + 2 OH−(aq)
Ogni mol di MgO dà 2 mol di OH−
n OH − = 2 ⋅ n MgO
Vsoluzione = 180 L
n H O + = 10
[H 3O + ] = 10 −2 M
−2
3
mol
⋅180 L = 1,8 mol
L
n H O + = n OH −
H3O+(aq
aq)) + OH (aq
aq)) → 2 H2O(l)
3
Neutralizzazione pH=7 (neutro)
n OH − = 1,8 mol
n MgO
ma
n OH − = 2 ⋅ n MgO
1
1
= ⋅ n OH − = ⋅1,8 mol = 0,9 mol
2
2
m MgO = n MgO ⋅ PM MgO
g
= 0,9 mol ⋅ 40,3044
≅ 36,27 g
mol
Tipologia di esercizio:
Acidi e basi forti
In una fossa d’irrigazione, una cisterna scarica abusivamente 1 m3 di
una soluzione di acido nitrico a pH=2. Con quanta acqua pura questo
scarto si deve miscelare perché il pH diventi 7? Quanta calce (CaO)
sarebbe bastata per neutralizzare preventivamente la soluzione?
Svolgimento:
acido nitrico (HNO3) elettrolita forte:
HNO3(aq) + H2O(l) → H3O+(aq) + NO3−(aq)
[HNO3 ]iniziale = [H 3O + ] = 10 − pH = 10 −2 M
Se il pH diventa 7
[H 3O + ] = 10 − pH = 10 −7 M = [HNO 3 ]finale
[HNO3 ]iniziale ⋅ Viniziale = [HNO3 ]finale ⋅ Vfinale
Viniziale
3
1000
dm
L
3
3
=1m =1m ⋅
⋅
= 1000 L
3
3
1m
dm
Considerando i volumi additivi
Vfinale = Viniziale + VH 2O
mol
mol
⋅1000 L = 10 −7
⋅ (1000 L + VH 2O )
L
L
−4
− 7 mol
10 mol = 10 mol + 10
⋅ VH 2O
L
10 mol − 10 −4 mol
VH 2O = 99999000 L
VH 2O =
− 7 mol
10
Circa 100 milioni di litri
L
Ovvero 10000 m3
10 − 2
Reazione di neutralizzare (reazione spostata a destra ha un K=1/Kw=10+14)
H3O+(aq
aq)) + OH (aq
aq)) → 2 H2O(l)
L’ossido di magnesio (CaO) fornisce l’OH−
CaO(s) + H2O(l)→ Ca(OH)2 → Ca2+(aq) + 2 OH−(aq)
Ogni mol di CaO dà 2 mol di OH−
n OH − = 2 ⋅ n CaO
!
Viniziale = 1000 L
n H O + = 10
[H 3O + ] = 10 −2 M
3
−2
mol
⋅1000 L = 10 mol
L
n H O + = n OH −
H3O+(aq
aq)) + OH (aq
aq)) → 2 H2O(l)
3
Neutralizzazione pH=7 (neutro)
n OH − = 10 mol
n CaO
ma
n OH − = 2 ⋅ n CaO
1
1
= ⋅ n OH − = ⋅10 mol = 5 mol
2
2
m CaO = n CaO ⋅ PM CaO
g
= 5 mol ⋅ 56,077
≅ 280,4 g
mol
Sarebbero bastati circa 280,4 g di calce (CaO) per
neutralizzare preventivamente la soluzione
!!!
Tipologia di esercizio:
Acidi e basi forti
In 100 litri di una soluzione di acido cloridrico a pH=2 si pongono
8,1 grammi di alluminio metallico. Determinare il pH della soluzione
al termine del processo che avviene (il volume rimane invariato).
Svolgimento:
acido cloridrico (HCl) elettrolita forte:
HCl(aq) + H2O(l) → H3O+(aq) + Cl-(aq)
[HCl] = [H + ] ≡ [H 3O + ] = 10 − pH = 1⋅10 −2 M
Vsoluzione = 100 L
n H + = n H O + = n HCl = [HCl] ⋅ Vsoluzione = 1⋅10 − 2
3
n Al =
mol
⋅100 L = 1 ,0 mol
L
m Al
8,1 g
=
≅ 0,30 mol
PA Al 26,981538 g
Tra l’alluminio metallico e l’HCl avviene la reazione redox:
6 HCl (aq) + 2 Al(s) → 3 H 2 (aq) + 2 AlCl3(aq)
O in forma ionica
6 H + (aq) + 2 Al(s) → 3 H 2 (aq) + 2 Al3+ (aq)
che potremmo anche scrivere così:
6 H 3O + (aq) + 2 Al(s) → 3 H 2 (aq) + 2Al3+ (aq) + 6 H 2 O (l)
Qualunque modo di scrivere la reazione si scelga si giungerà al medesimo
risultato:
6H
mol iniziali)
Variazione di mol)
mol finali)
+
(aq)
+ 2 Al(s) → 3 H 2 (aq) + 2 Al
1,0
0,3
6
− 0,3 ⋅
2
0,1
[H 3O + ]finale ≡ [H + ]finale =
n H+
− 0,3
-finale
Vsoluzione
=
3+
--
--
3
+ 0,3 ⋅
2
0,45
+ 0,3
0,1 mol
mol
= 1⋅10 −3
L
100 L
pH = −log10 [H 3 O + ] = −log10 [1 ⋅10 −3 ] = 3
0,3
(aq)
Tipologia di esercizio:
Acidi e basi forti
Esercizi simili. Prova tu!!!
☺In una cisterna che contiene 12,50 m3 di acqua vengono aggiunti 3,650 kg di
acido cloridrico. Calcolare il pH della soluzione. Determinare la massa di
idrossido di calcio necessaria per neutralizzare la soluzione.
(R. pH = 2,096; ~4,509 kg)
☺
A 50 mL di una soluzione acquosa di acido nitrico di concentrazione
incognita, si aggiungono 125 mL di una soluzione di idrossido di bario 10−2 M. La
soluzione risultante è neutra:
2 HNO3 (aq) + Ba(OH)2 (aq) → Ba(NO3)2 (aq) + 2 H2O (aq)
determinare la concentrazione iniziale dell'acido.
(R. [HNO3]=5·10-2 M)
☺
In 300 L di acqua vengono sciolti 67,327 g di KOH. Calcolare il pH della
soluzione. Quanti litri di una soluzione 0,5 M di acido cloridrico occorre
aggiungere alla soluzione per ridurre a 7 il valore di pH?
(R. pH = 11,60; 2,4 L )
Tipologia di esercizio:
acidi deboli o basi deboli
Calcolare il pH di una soluzione 0,1 M di HIO4 (Ka=2,3·10-2 mol/L)
L'acido periodico è un acido monoprotico non troppo debole; ovvero il valore della
costante di trasferimento protonico non è troppo piccolo. Si può scrivere:
Svolgimento:
i)
eq)
−
HIO4(aq) + H2O(l) ⇄ IO4-(aq) + H3O+(aq)
Ca
Ca – x
x
x
[IO4 ] ⋅ [H 3O + ]
Ka =
= 2,3 ⋅ 10− 2
[HIO4 ]
x2
Ka =
Ca − x
Ca
0,1
=
≈ 4,35 < 380 ⇒ α > 0,05
−2
K a 2,3 ⋅10
Cioè più del 5% di HIO4 si ionizza, vale a dire non posso trascura la x al
denominatore nell'equazione della costante di equilibrio:
2
x
Ka =
Ca − x
Dobbiamo risolvere l’equazione di secondo grado:
x2 + Ka x - KaCa = 0
x 2 + 2,3 ⋅10 −2 x − 2,3 ⋅10 −2 ⋅ 0,1 = 0
x 2 + 2,3 ⋅10 −2 x − 2,3 ⋅10 −3 = 0
− 2,3 ⋅10 −2 + (−2,3 ⋅10 − 2 ) 2 + 4 ⋅ 2,3 ⋅10 −3
x = [H 3 O ] =
≅ 3,782 ⋅10 − 2 [mol/L]
2
+
pH = −log10 [H 3 O + ] = −log10 [3,782 ⋅10 −2 ] ≅ +1,42
Se il valore di x fosse stato trascurato rispetto a 0,1 M (Ca)
nell'equazione della costante di equilibrio si sarebbe ottenuto:
[H 3 O + ] = 2,3 ⋅ 10−2 ⋅ 0,1 = 2,3 ⋅ 10−2 ≅ 4,796 ⋅ 10−2
pH = −log10 [4,796 ⋅10 −2 ] ≅ +1,32
Avremmo commesso un errore dell’ordine del 7% sul pH e di oltre il
20% sulla concentrazione di H3O+ !!!
Tipologia di esercizio:
acidi deboli o basi deboli
Calcolare le concentrazioni di HA, H+ e A- e il pH di una soluzione
0,10 mol/L di un acido monoprotico debole, HA, con Ka=1,4·10-5
Svolgimento:
HA(aq) + H2O(l)
Conc. iniziali
0,10
Variazioni
-x
Concentrazioni
all’equilibrio
H3O+ (aq) + A-(aq)
-
0,10-x
-
+x
+x
x
x
Dall’equazione della costante di equilibrio si ha:
[H + ] [A - ]
Ka =
[HA]
Ca
> 380
Ka
2
x
1,4 ×10-5 =
0,10 - x
⇒ α > 0,05 ⇒ C a − x = 0,10 − x ≅ 0,10
2
x
1,4 ×10-5 =
0,10 - x
2
x
1,4 ×10-5 =
0,10
x2 = 1,4·10-5· 0,10 = 1,4×10-6
x = 1,4 × 10 -6 = 1,2 × 10 -3 M
Verifichiamo innanzitutto l’approssimazione fatta:
x = 0,0012 << 0,10
0,10-x = 0,10 - 0,0012 = 0,0998 ≈ 0,10
Le concentrazioni all’equilibrio sono quindi:
[H3O+] = x = 1,2×10-3 M
[A-] = x = 1,2·10-3
[HA] = 0,10 - x = 0,0998 ≈ 0,10
pH = -log(1,2×10-3 )=2,92
Talvolta per gli acidi deboli
ionizzazione
o le basi deboli si richiede il grado di
Grado di ionizzazione
Il grado di ionizzazione di un acido (o base) è definito come il rapporto
fra la concentrazione di acido (base) ionizzato all’equilibrio e la
concentrazione totale presente inizialmente. Moltiplicato per 100
corrisponde alla percentuale di acido (base) che è ionizzato
all’equilibrio.
Nel caso precedente si ha:
[A − ] [A − ] 1,2 × 10-3
=
=
= 1,2 ×10-2
grado di ionizzazione =
[HA] 0
Ca
0,10
% ionizzazione = 1,2×10-2 × 100 = 1,2%
Tipologia di esercizio:
acidi deboli o basi deboli
Calcolare le concentrazioni di tutte le specie e il pH di una soluzione 0,10 M
di metilammina (Kb=4,3×10-4).
Svolgimento:
CH3NH2(aq) + H20(l)
CH3NH3+ (aq) + OH-(aq)
Conc. iniziali
0,10
Variazioni
-x
+x
+x
0,10-x
x
x
Concentrazioni
all’equilibrio
0
~0
+
[CH
NH
]
[OH
]
3
3
Dall’equazione della costante di equilibrio si ha:
Kb =
2
[CH 3 NH 2 ]
C
0,10
x
b
=
≤ 380
4,3 ×10 −5 =
-4
K b 4,3 ⋅10
0,10 - x
⇒ 4,3 ×10-4 ⋅ (0,10 - x ) = x 2 ⇒ = x 2 + 4,3 ×10 −4 x − 4,3 ×10 −5 = 0
x = [OH − ] =
− 4,3 × 10 − 4 +
(4,3 ×10 )
−4 2
2
+ 4 ⋅ 4,3 × 10 −5
 mol 
= 6,346 × 10 −3 
 L 
Le concentrazioni all’equilibrio sono quindi:
[OH-] = x = 6,346×10-3 M
[CH3NH3+] = x = 6,346×10-3 M
[CH3NH2] = 0,10 - x = 0,10 - 6,6×10-3 = 0,09354
Il calcolo non dà direttamente [H3O+] e per calcolare il pH
conviene prima calcolare il pOH e poi sottrarre a 14
pOH = -log(6,6×
×10-3 ) ≈ 2,2
pH = 14-pOH=14-2,2 = 11,8
Il grado di ionizzazione di tale base vale:
grado di ionizzazione =
[BH + ] [BH + ] 6,6 × 10-3 M
=
=
= 6,346 × 10- 2
[B]0
Cb
0,10 M
% ionizzazione = 6,346×
×10-2 × 100 = 6,346 %
Tipologia di esercizio:
acidi deboli o basi deboli
Svolgimento:
TABELLA 15.1
Costanti di dissociazione
di acidi deboli.
(i)
(eq)
−
+
HF(aq) + H2O(l) ⇄ F-(aq) + H3O+(aq)
Ca
Ca – x
x
x
[F ] ⋅ [H 3O ]
Ka =
= 6,31⋅10 − 4 M
[HF]
x2
Ka =
Ca − x
Punto c)
Ca
0,4
=
≈ 634 > 380 ⇒ α < 0,05 ⇒ x << C a
−4
K a 6,31 ⋅10
Possiamo
effettuare questa
approssimazione:
+
[ H 3O ] = K a ⋅ C a
+
−4
[H 3 O ] = 6,31⋅10 ⋅ 0,40 = 2,524 ⋅10
−4
pH = −log10 [H 3O ] = −log10 [ 2,524 ⋅ 10 ] ≅ + 1,80
+
−4
Punto d)
Ca
0,01
=
≈ 15,85 < 380 ⇒ α > 0,05
−4
K a 6,31 ⋅10
Dobbiamo risolvere l’equazione di secondo grado:
x 2 + K a x - K aC a = 0
x 2 + 6,31 ⋅10 −4 x − 6,31 ⋅10 −4 ⋅ 0,01 = 0
x 2 + 6,31 ⋅10 − 4 x − 6,31 ⋅10 −6 = 0
−4
−4 2
−6
6,31
⋅
10
+
(
−
6,31
⋅
10
)
+
4
⋅
6,31
⋅
10
x = [H 3 O + ] =
≅ 2,22 ⋅10 −3
2
pH = −log10[H 3O ] = −log10[2,22 ⋅ 10 ] = +2,65
+
−3
Se avessi usato l’equazione approssimata:
[H 3 O + ] = 6,31⋅10 −4 ⋅ 0,01 = 6,31⋅10 −6 ≅ 2,51⋅10 −3
pH = −log10 [2,51⋅10 −3 ] = +2,60
Errore di ~ 2%
Terminare l’esercizio da soli (punti a,b,e) prendendo le Ka dalla Tab.15.1
Tipologia di esercizio:
n NH =
3
VNH
V
3
molare a c.n.
=
2,8 l
l
22,414
mol
acidi deboli o basi deboli
Svolgimento:
≅ 0,125 mol ⇒
[NH ] = C
3
b
=
n NH
V
3
soluzione
=
0,125 mol
= 0,1 M
1,25 l
NH3(aq) + H2O(l) ⇄ NH4+(aq) + OH-(aq)
eq) Cb – x
x
x
[NH 4+ ] ⋅ [OH − ]
Kb =
= 1,8 ⋅10 −5 M
[NH 3 ]
Cb
0,1
+3
=
≈
5,56
⋅
10
> 380
−5
K b 1,8 ⋅10
x = [OH-] = [NH4+]
x2
Kb =
(C b − x)
⇒ [OH − ] = K b ⋅ C b
pOH = -log10 [OH − ] = -log10 [ K b ⋅ C b ] = -log10 [ 1,8 ⋅10 −5 ⋅ 0,1 ]
pH = 14 - pOH = 14 + log 10 [ 1,8 ⋅10 −5 ⋅ 0,1 ] ≅ 11,13
Terminare l’esercizio da soli (punti b,c) prendendo la
Kb
di CH3NH2 dalla Tab.15.2
Tipologia di esercizio:
acidi deboli e basi deboli
Svolgimento:
L’acido benzoico è un acido organico monoprotico debole: HA
(i)
(eq)
−
HA(aq) + H2O(l) ⇄ A-(aq) + H3O+(aq)
Ca
----x
x
Ca – x
+
2
[A ] ⋅ [H 3O ]
Ka =
[HA]
x
Ka =
Ca − x
x = [A-] = [H3O+] = 10-pH = 10-2,95 = 1,112·10-3 M
(
)
−3 2
x
1,112 ⋅10
−5
Ka =
=
≅
6,67
⋅
10
M
−3
C a − x (0,02 − 1,112 ⋅10 )
2
Tipologia di esercizio:
Acidi poliprotici
Svolgimento:
Punto c)
Come se fosse H2SO3
H2SO3(aq) + H2O(l) ⇄ HSO3-(aq) + H3O+(aq)
Ka1 = 1,41·10-2
HSO3-(aq) + H2O(l) ⇄ SO32-(aq) + H3O+(aq)
Ka2 = 6,31·10-8
Oppure per la prima dissociazione si scrive:
SO2(aq) + 2H2O(l) ⇄ HSO3-(aq) + H3O+(aq)
Ka1 = 1,41×10-2
Bisogna calcolare la concentrazione di SO2(aq) che coincide con quella di H2SO3
Vmolare a c.n
L
V
= 22,414
=
mol n
[SO 2 (aq)] ≡ [H 2SO 3 ] =
⇒ n SO 2 =
n SO 2
VSoluzione
=
VSO 2
L
22,414
mol
K a,1 =
4,5 L
L
22,414
mol
≅ 0,200 mol
0,200 mol
mol
= 0,1
2,0 L
L
SO2(aq) + 2 H2O(l) ⇄ HSO3−(aq) + H3O+(aq)
Ca
Ca – x
x
x
−
3
=
+
[HSO ] ⋅ [H 3O ]
= 1,41⋅10 − 2
[SO 2 ]
Ca
0,1
=
≈ 7,09 < 380 ⇒
−2
K a 1,41 ⋅10
x = [HSO 3− ] = [H 3O + ]
x2
K a,1 =
(Ca − x)
Non possiamo trascurare la x
x 2 + K a,1 ⋅ x − K a,1 ⋅ C a = 0
x 2 + 1,41 ⋅10 −2 ⋅ x − 1,41 ⋅10 −3 = 0
x = [H 3O + ] =
−2
− 1,41⋅10 +
(1,41⋅10 )
−2 2
+ 4 ⋅1,41⋅10 −3
2
= 3,116 ⋅10 − 2
pH = −log 10 [H 3O + ] = −log 10 [3,116 ⋅10 −2 ] ≅ +1,51
Punto d) una soluzione che contiene 210 mg di H3AsO4 in 500 mL d’acqua
H3AsO4(aq) + H2O(l) ⇄ H2AsO4−(aq) + H3O+(aq)
Ka1 = 5,49·10−3
H2AsO4-(aq) + H2O(l) ⇄ HAsO42−(aq) + H3O+(aq)
Ka2 = 1,74·10−7
HAsO42−(aq) + H2O(l) ⇄ AsO43−(aq) + H3O+(aq)
Ka3 = 5,13·10−12
m H 3AsO4
[H 3AsO 4 ] =
n H 3AsO4
Vsoluzione
=
PM H 3AsO4
Vsoluzione
0,210 g
141,9430 g/mol
=
≅ 2,96 ⋅10 −3 M = C a
0,5 L
K a,1
K a,2
5,49·10−3
+4
+3
=
=
3,15
⋅
10
>
10
1,74·10−7
H3AsO4(aq) + H2O(l)
i)
Ca
Eq) Ca – x
−
4
+
[H 2 AsO ] ⋅ [H 3O ]
K a,1 =
= 5,49 ⋅10 −3
[H 2 AsO4 ]
H2AsO4−(aq) + H3O+(aq)
x
x
x2
K a,1 =
(Ca − x)
Ca
2,96·10−3
=
≤ 380 ⇒Non possiamo trascurare la x
−3
K a,1 5,49·10
x 2 + 5,49 ⋅10 −3 ⋅ x − 1,62504 ⋅10 −5 = 0
x 2 + K a,1 ⋅ x − K a,1 ⋅ C a = 0
+
x = [H 3O ] =
− 5,49 ⋅10 −3 +
(5,49 ⋅10 )
−3 2
+ 4 ⋅1,60728 ⋅10 −5
2
≅ 2,132 ⋅10 −3
pH = −log 10 [H 3O + ] = −log 10 [2,132 ⋅10 −3 ] ≅ +2,67
Terminare l’esercizio da soli (punti a,b,e) prendendo le costanti dalla Tab.15.1
Tipologia di esercizio:
Svolgimento:
Punto a)
CH3COOK(aq) → CH3COO-(aq) + K+(aq)
(i)
(eq)
Idrolisi
CH3COO- (aq) + H2O(l) ⇄
CS
CS-x
[CH3COOK] = [CH3COO-] = CS
CH3COOH(aq) + OH- (aq)
--x
--x
2
−
K W 1 ⋅10 −14
[CH
COOH]
⋅
[OH
]
x
−10
3
Ki = Kb =
=
=
5,55
⋅
10
=
=
−5
−
K a 1,8 ⋅10
[CH 3COO ]
Cs − x
CS
KW
0,15
+8
−
=
≅
2,7
⋅
10
>
380
⇒
x
=
[OH
]
=
K
⋅
C
=
⋅ CS
b
S
-10
K b 5,55 ⋅10
Ka
 KW

⋅ CS 
pOH = −log10 [OH ] = −log10 [ K b ⋅ CS ] = −log10 
 Ka

−
 KW

⋅ CS 
pH = 14 − pOH = 14 + log10 
 Ka

 1⋅10 -14

 KW


pH = 14 + log10 
⋅ CS  = 14 + log10
⋅ 0,15  ≅ 8,96
5
 1,8 ⋅10

 Ka



Il pH è basico (come atteso)
Punto c) una soluzione di Na2HPO3 al 10%w di densità d = 1,08 g/ml
Na2HPO3 in acqua è completamente dissociato:
Na2HPO3 (aq)
2 Na+ (aq) + HPO32- (aq)
HPO32- (anione fosfito) è la base coniugata di H2PO3- (anione idrogenofosfito)
L’ HPO32- (anione fosfito) è soggetto ad idrolisi (basica) secondo l’equilibrio:
HPO32- + H20 ⇄ H2PO3- + 0H-
KW
K idrolisi,1 = K b =
Ka
Quale Ka bisogna usare? La Ka2 dell’acido fosforoso (H3PO3)
H3PO3(aq) + H2O(l) ⇄ H2PO3-(aq) + H3O+(aq)
‾(aq)
H2PO3
i)
eq)
+ H2O(l) ⇄ H2PO3
2-(aq)
O+(aq)
+ H3
HPO32- + H20 ⇄ H2PO3- + 0HCs
----Cs-x
x
x
Ka1 = 5,0·10-2
Ka2 =
2,0·10-7
[H 2 PO 3− ]eq = [OH − ]eq = x
[HPO 32− ]eq = CS − x
−
−
[H
PO
][OH
]
K W 1,0 ⋅10 −14
2
3
−8
K idrolisi = K b =
=
= 5 ⋅10 =
−7
K a,2 2,0 ⋅10
[HPO 32− ]
x2
5,0 ⋅10 =
CS − x
−8
Dalla tabella 15.1
CS = ?
Ricordiamo che dalla percentuale in peso alla molarità di una soluzione ci si
può arrivare direttamente usando la formula:
 ml   g  C%
1000  ⋅ d
⋅
L
mL
  
 100
[C] =
 g 
PM

mol


purché la
densità sia
espressa in
g/mL
(si veda la lezione #10)
 ml 
 g  10
1000  ⋅1,08   ⋅
 l 
 ml  100 ≅ 0,857 M
CS = [Na 2 HPO 3 ] =
 g 
125,9549 

 mol 
2
CS
CS 0,857
x
+8
=
=
= 1,714 ⋅10 > 380 ⇒ 2,128 ⋅10 − 4 =
−8
K idrolisi K b 5 ⋅10
CS
x = [OH − ] = K b ⋅ CS = 5 ⋅10 −8 ⋅ 0,857
pOH = -log10 [OH − ] = −log10 [ 5 ⋅10 −8 ⋅ 0,857 ]
pH = 14 − pOH = 14 + log10 [ 5 ⋅10 −8 ⋅ 0,857 ]
pH ≅ 10,32
Il pH è basico (come atteso)
Punto e) una soluzione di acetato di sodio avente frazione molare χ= 1,8 · 10–4 e
densità d = 1,0 g/ml
CH3COONa(aq) → CH3COO-(aq) + Na+(aq)
(i)
(eq)
CH3COO- (aq) + H2O(l)
[CH3COONa] = [CH3COO-] = Cs
CH3COOH(aq) + OH- (aq)
Cs
Cs-x
--x
--x
−
2
K W 1 ⋅10 −14
[CH
COOH]
[OH
]
x
⋅
−10
3
Ki = Kb =
=
=
5,55
⋅
10
=
=
−5
−
K a 1,8 ⋅10
[CH 3COO ]
Cs − x
1,8•10-4 mol di CH3COONa
1 mol di soluzione
0,99982 mol di H2O
m CH COONa = n CH COONa ⋅ PM CH COONa = 1,8 ⋅ 10 -4 mol ⋅ 82,03427
3
3
3
m H O = n H O ⋅ PM H O = 0,99982 mol ⋅ 18,0152
2
2
2
g
≅ 0,001477 g
mol
g
≅ 18,0120 g
mol
Vsoluzione
m CH 3COONa + m H 2O 0,001477 g + 18,0120 g
m soluzione
=
=
=
≅ 18,0135 ml = 0,0180135 [L]
g
d
d
1,0
mL
[CH 3 COONa ] ≡ [CH 3 COO
-
]=
n CH 3COONa
Vsoluzione
CS
0,01
+7
=
=
1,8
⋅
10
> 380
-10
K b 5,55 ⋅10
−
pOH = -log10 [OH ] = -log10 [

pH = 14 - pOH = 14 + log10 


1,8 ⋅ 10 -4 [mol]
=
≅ 0,010 M
0,0180135 [L ]
⇒ [OH − ] = K b ⋅ CS =
KW
⋅ CS
Ka
 KW

K b ⋅ C S ] = -log10 
⋅ CS 
 K

a



KW
⋅ CS 

Ka

 1 ⋅ 10 -14

 KW


 ≅ 8,37
pH = 14 + log10 
⋅ C S  = 14 + log10
⋅
0,01
 K


 1,8 ⋅ 10 -5
a




Il pH è basico (come atteso)
Terminare l’esercizio da soli (punti b,d) prendendo le costanti dalla Tab.15.1
Tipologia di esercizio:
Idrolisi
Calcolare il pH di una soluzione 5·10-2M di cloruro di
ammonio (Kb,NH3 = 1,8·10-5 mol/L).
Il cloruro di ammonio (NH4Cl) è un sale che in acqua è completamente dissociato
in catione ammonio (NH4+) e anione cloruro (Cl−). Lo ione ammonio (NH4+), che è
presente nella soluzione, ha proprietà acide (è l'acido debole coniugato della
base debole ammoniaca, NH3) ed è soggetto a reazione di idrolisi (acida):
NH4Cl(aq) →NH4+(aq)+ Cl−(aq)
(i)
(eq)
NH4+(aq) + H2O(l)
CS
CS – x
NH3(aq) + H3O+(aq)
----x
x
K W [NH 3 ] [H 3O + ]
costante d' idrolisi = K i = K a =
=
Kb
[NH 4+ ]
K W 1,0 ⋅10 −14
x2
−10
=
= 5,55 ⋅10 =
−5
K b 1,8 ⋅10
(CS − x)
Cs
5 ⋅10 −2
=
> 380 ⇒
−10
K a 5,55 ⋅10
Cioè meno del 5% di NH4+ si idrolizza
CS − x ≅ CS
+
[H 3O + ]2
Ka =
CS
[H 3O ] = K a ⋅ CS = 5,55 ⋅10
−10
⋅ 5,0 ⋅10
−2
pH = −log 10 [H 3O + ] = −log 10 [ 5,55 ⋅10 −10 ⋅ 5,0 ⋅10 −2 ] ≅ +5,28
Tipologia di esercizio:
Ca(CH3COO)2(aq) → 2 CH3COO-(aq)
Svolgimento:
+ Ca++(aq)
Cs = [CH3COO-] = 2•[Ca(CH3COO)2]=2• [Ca++]
CH3COOH(aq) + H2O(l)
(i)
Ca
m Ca(CH3COO) 2
Vsoluzione
CH3COO-(aq) + H3O+(aq)
Cs+x
Innanzitutto, calcoliamo Cs e Ca:
CS = 2 ⋅
Ca = [CH3COOH]
Cs
(eq) Ca−x
n Ca(CH3COO) 2
= 2⋅
Tampone
PM Ca(CH3COO) 2
Vsoluzione
--x
15,8 [g ]

158,169 g
0,1 [mol]
 mol
= 2⋅
≅ 2⋅
= 0,4 M
0,5 [L]
0,5 [L]
m CH COOH
3
Ca =
n CH COOH
3
Vsoluzione
m CH COOH
3
=
PM CH COOH
3
Vsoluzione
% w CH 3 COOH
% w CH 3 COOH
=
⋅ m soluzione =
⋅ Vsoluzione ⋅ d =
100
100
1,2
g
=
⋅ 500 [ml] ⋅ 1,0   = 6,0 [g ]
100
 ml 
m CH COOH
3
Ca =
n CH COOH
3
Vsoluzione
=
PM CH COOH
3
Vsoluzione
C a 0,2
0,1 <
=
= 0,5 < 10
Cs 0,4
6,0 [g ]

60,0524  g
 mol 0,1 [mol]
=
=
= 0,2 M
0,5 [l]
0,5 [l]
Abbiamo un tampone
e possiamo trascurare la x
[CH 3COO − ] [H 3O + ] (Cs + x)x
Ka =
=
[CH 3COOH]
(Ca − x)
na
n
C [H O ]
C
Ka ≅ s 3
⇒ [H 3O + ] ≅ K a a = K a V = K a a
ns
Ca
ns
Cs
V
+
Ca
pH = −log 10[H 3O ] = −log 10[K a
]
Cs
+
0,2
= −log 10[1,8 ⋅10 ⋅
] = + 5,05
0,4
-5
Oppure
na
pH = −log 10[H 3O ] = −log 10[K a ]
ns
+
0,1
= −log 10[1,8 ⋅10 ⋅
] = + 5,05
0,2
-5
Tipologia di esercizio:
Tampone (esempio di preparazione)
Svolgimento:
acido debole + base forte → sale + acqua
CH3COO
COOH
H(aq) + NaOH
NaOH(aq) → CH3COONa(aq) + H2O(aq)
meglio in forma ionica:
CH3COO
COOH
H(aq) + OH-(aq) → CH3COO-(aq) + H2O(aq)
La reazione avviene completamente (spostata a destra: irreversibile) perché ha
una costante molto grande (è l’inverso della costante di idrolisi basica
1/Ki=Ka/KW≈1,8·10+9).
Ricorda il forte (NaOH: base forte) sposta completamente il debole (CH3COOH: acido debole)
Calcoliamo le moli di acido debole (CH3COOH) e di base forte (NaOH).
Il numero di moli di acido acetico contenuto in 400 ml di soluzione 0,0010 M è
n CH 3COOH = [CH 3COOH]⋅ Vsoluzione,CH 3COOH
mol
= 0,001
⋅ 0,400 l = 4 ⋅10 − 4 [mol ]
L
Il numero di moli di idrossido di sodio contenuto in 500 ml di soluzione 0,00040 M è
n NaOH = [NaOH]⋅ Vsoluzione,NaOH = 0,0004
mol
⋅ 0,500 l = 2 ⋅10 − 4 [mol ] ≡ n OH −
L
Moli
i)
CH3COO
COOH
H(aq) + OH-(aq) → CH3COO-(aq) + H2O(aq)
4•10-4
2•10-4
---
∆)
-2•10-4
Moli
f) 2•10-4
-2•10-4
+2•10-4
+2•10-4
0
2•10-4
2•10-4
Abbiamo un tampone: 0,1< na/ns<10
CH3COOH(aq) + H2O(l) ⇄ CH3COO−(aq) + H3O+(aq)
(i)
Ca
CS
--x
CS+x
(eq) Ca-x
na
-4
CS [H 3O ]
Ca
n
2
⋅
10
+
Ka ≅
⇒ [H 3O ] ≅ K a
= Ka V = Ka a = Ka
nS
Ca
CS
nS
2 ⋅10 -4
V
+
pH = −log10[H 3O ] = −log10[K a ] = −log10[1,8 ⋅ 10 ] = + 4,74
+
-5
Tipologia di esercizio con
Acido debole libero; Tampone; idrolisi (basica)
Ovvero preparazione di un tampone e sua successiva distruzione (“morte”)
Esercizio
A 160 ml di una soluzione 0,01 M di acido formico (HCOOH) si fanno due
aggiunte successive di 40 mL di idrossido di sodio (NaOH) 0,02 M.
Calcolare il pH della soluzione iniziale di HCOOH e il pH delle soluzioni
ottenute in seguito a ciascuna aggiunta di NaOH. (La costante di
dissociazione dell’acido formico è Ka = 1,8·10–4 mol/L e si ritengano,
inoltre, i volumi additivi).
Svolgimento:
pH della soluzione iniziale di HCOOH
HCOOH (aq) + H2O(l) ⇄ HCOO-(aq) + H3O+(aq)
(i)
Ca
(eq)
Ca−x
---
----
x
x
x = [HCOO − ] = [H 3O + ]
−
+
[HCOO ] ⋅ [H 3O ]
Ka =
[HA]
x2
Ka =
Ca − x
Ca
0,01
=
< 380
–4
K a 1,8·10
⇒ α > 0,05
Cioè più del 5% di HCOOH si ionizza, vale a dire non posso trascura la x al
denominatore nell'equazione della costante di equilibrio
K a ⋅ (C a − x ) = x 2
x2
Ka =
Ca − x
x 2 + K a x − K a Ca = 0
x = [H 3O + ] =
− Ka +
(K a )2 + 4K a Ca
2
=
− 1,8 ⋅10 −4 + 3,24 ⋅10 −8 + 4 ⋅1,8 ⋅10 −4 ⋅1⋅10 − 2
=
≅ 1,255 ⋅10 −3 M
2
pH = −log 10 [H 3O + ] = −log 10[1,255 ⋅10 −3 ] = + 2,90
Prima aggiunta di 40 mL di idrossido di sodio (NaOH) 0,02 M.
HCOOH
HCOO
H(aq) + NaOH
NaOH(aq) → HCOONa(aq) + H2O(aq)
meglio in forma ionica:
HCOOH
HCOO
H(aq) + OH-(aq) → HCOO-(aq) + H2O(aq)
La reazione avviene completamente (spostata a destra: irreversibile) perché ha
una costante molto grande (è l’inverso della costante di idrolisi basica
1/Ki=Ka/KW≈1,8·10+10).
Ricorda il forte (NaOH: base forte) sposta completamente il debole (HCOOH: acido debole)
n OH − = n NaOH = C NaOH ⋅ VNaOH = 0,02 (mol/L ) ⋅ 0,040 L = 0,0008 mol
n HCOOH = C HCOOH ⋅ VHCOOH = 0,01 (mol/L ) ⋅ 0,160 L = 0,0016 mol
Moli
OH−
+ HCOOH
Iniziali
0,0008
0,0016
0
variazione
-0,0008
-0,0008
+0,0008
Totale fine
reazione
0
0,0008
0,0008
Abbiamo un tampone
n
0,1 < a < 10
ns
→
Quindi
HCOO−
[H 3O + ] = K a
+ H2O
na
ns
na
- 4 0,0008
pH = −log10 [H 3O ] = −log10 [K a ] = −log10 [1,8 ⋅10 ⋅
]
ns
0,0008
+
pH = −log 10 [1,8 ⋅10 -4 ] = pKa ≅ +3,745
Seconda aggiunta di 40 mL di idrossido di sodio (NaOH) 0,02 M.
n OH − = n NaOH = C NaOH ⋅ VNaOH = 0,02 (mol/L ) ⋅ 0,040 L = 0,0008 mol
n HCOO − = 0,0008 mol
n HCOOH residuo = 0,0008 mol
Moli
OH−
+ HCOOH
Iniziali
0,0008
0,0008
0,0008
variazione
-0,0008
-0,0008
+0,0008
Totale fine
reazione
0
0
0,0016
→
HCOO−
+ H2O
Non abbiamo più il tampone
Abbiamo una soluzione di anione formiato (HCOO-)
Considerando i volumi additivi:
[HCOO ] =
−
n HCOO−
Vtotale
=
n HCOO−
V1 + V2 + V3
=
0,0016 [mol ]
= 8 ⋅10 −3 M = CS
(0,160 + 0,040 + 0,040) [L]
dà idrolisi basica perché esso è la base coniugata di una acido debole (HCOOH)
(i)
(eq)
HCOO- (aq) + H2O(l) ⇄
CS
CS-x
HCOOH(aq) + OH- (aq)
--x
--x
x = [HCOOH] = [OH − ]
K W 1⋅10 −14
[HCOOH] ⋅ [OH − ]
x2
−11
Ki = K b =
=
= 5,55 ⋅10 =
=
−4
−
K a 1,8 ⋅10
[HCOO ]
Cs − x
KW
CS 7,754 ⋅10 −3
−
=
>
380
⇒
x
=
[OH
]
=
K
⋅
C
=
⋅ CS
b
S
-11
K b 5,55 ⋅10
Ka
−
pOH = -log10 [OH ] = -log10 [

pH = 14 - pOH = 14 + log10 

 KW


K b ⋅ CS ] = -log10 
⋅ CS 
 Ka


KW
⋅ CS 
Ka

 1⋅10-14

 KW

−
3
pH = 14 + log 10 
⋅ CS  = 14 + log 10 
⋅ 8 ⋅10  ≅ 7,82
4
 1,8 ⋅10

 Ka



Esercizio simile da studiare per bene a pag. 519-521 del libro
di testo (Nobile-Mastrorilli)
Tipologia di esercizio:
Tampone
Calcolare quanti millilitri di una soluzione 0,12 M di cloruro di ammonio
si devono aggiungere a 100 mL di ammoniaca 0,2 M per ottenere una
soluzione tampone avente pH=9,72. Per l’ammoniaca, Kb = 1,8·10−5 M.
Svolgimento:
NH3(aq
3(aq)) + H2O(l) ⇄
(i) Cb
(eq) Cb−x
[NH +4 ] ⋅ [OH − ]
Kb =
= 1,8·10−5 M
[NH 3 ]
NH4+(aq
+
OH
aq))
(aq
aq))
Cs
Cs+x
x
Per un tampone base debole/acido coniugato:
nb
n NH3
Cb −x
Cb
nb
−
V
[OH ] = K b ⋅
≅ Kb ⋅
= Kb ⋅
= Kb ⋅
= Kb ⋅
ns
Cs + x
Cs
ns
n NH +
4
V
pH = 9,72 ⇒ pOH = 14 − 9,72 = 4,28 ⇒ [OH − ] = 1⋅10 −4,28 M
−
[OH ] = K b ⋅
n NH3
n NH +
1⋅10
4
− 4,28
−5
= 1,8 ⋅10 ⋅
n NH3
n NH +
4
n NH 3 = [NH 3 ] ⋅ Vsoluzione, NH 3 = 0,2 (mol/L) ⋅ 0,1 (L) = 0,02 mol
n NH + = [NH 4 Cl] ⋅ Vsoluzione, NH 4Cl = 0,12 (mol/L) ⋅ Vx (L)
4
1⋅10 − 4,28 = 1,8 ⋅10 −5 ⋅
0,02
0,12 ⋅ Vx
1,8 ⋅10 −5 0,02
Vx =
⋅
≅ 0,05716 L = 57,16 mL
− 4,28
1⋅10
0,12
Vx (L) = ?
Tipologia di esercizio con
idrolisi (acida); Tampone
Svolgimento:
acido forte + base debole (tipo ammoniaca) →
HX(aq)
Nel caso in esame:
+
HCl(aq) +
oppure in forma ionica:
Ovvero:
:B(aq)
CH3NH2(aq)
→
→
sale
BHX(aq)
CH3NH3Cl(aq)
H+(aq) + CH3NH2(aq) → CH3NH3+(aq)
H3O+(aq) + CH3NH2(aq) → CH3NH3+(aq) + H2O(aq)
Calcoliamo le moli di base debole (CH3NH2) e di acido forte (HCl).
Il numero di moli di CH3NH2 contenuto in 50 mL di soluzione 2,0M è
n CH NH = [CH3 NH 2 ] ⋅ Vsoluzione,CH NH
3
2
3
2
mol
= 2,0
⋅ 0,050 l = 0,1 [mol ]
l
Il numero di moli di HCl contenuto in 50 mL di soluzione al 7,0% in peso
(d= 1,03 g/ml) è
n HCl = [HCl] ⋅ Vsoluzione,HCl
Ma, bisogna calcolarla?
m HCl
n HCl
% w HCl
=
⋅ Vsoluzione,HCl ⋅ d
100
n HCl
m HCl
=
PM HCl
7,0
g
% w HCl
[
]
⋅
50
ml
⋅
1,03
⋅ Vsoluzione,HCl ⋅ d
 ml 
100
100
=
=
≅ 0,1 [mol]
PMHCl
 g 
36,4609 
 mol 
n HCl = n H O = 0,1 [mol ]
3
+
1° aggiunta:
H3O+(aq) + CH3NH2(aq) →
Moli
i) 0,1
∆)
-0,1
f)
0
H2O(aq)
+ CH3NH3+(aq)
0,1
--
--
-0,1
+0,1
+0,1
0
0,1
0,1
Abbiamo una soluzione di ione metilammonio
Considerando i volumi additivi:
[CH NH ] =
3
+
3
n CH NH+
3
Vtotale
3
0,1 [mol ]
=
=
= 1,0 M
V1 + V2 (0,050 + 0,050) [L]
n CH NH+
3
3
dà idrolisi acida perché esso è l’acido coniugato di una base debole: CH3NH2
Idrolisi acida:
(i)
(eq)
CH3NH3+(aq
aq)) + H2O(
O(ll)
CS
CS-x
Ki = Ka =
x
x
KW
x2
=
K b Cs − x
+
K W [CH 3 NH 2 ] ⋅ [H 3O ]
=
Kb
[CH 3 NH 3+ ]
Cs
C
1
= s =
> 380
−14
K
1,0 ⋅10
Ki
W
Kb
4,26 · 10 – 4
CH3NH2(aq
aq)) + H3O+(aq
aq))
------
x << Cs
KW
x = [H 3O ] =
⋅ Cs
Kb
+
 KW

⋅ Cs  =
pH = −log10[H 3O ] = −log10 
 Kb

+
 1,0 ⋅ 10 −14

= −log10 
⋅ 1,0  = 5,31
–4
 4,26 · 10

2° aggiunta:
H3O+(aq) + CH3NH2(aq)
Moli
i) 0
0,1
H2O(l)
+ CH3NH3+(aq)
0
0,1
Abbiamo un tampone: 0,1< nb/ns<10
+
CH3NH2(
+
H
O
⇄
CH
NH
+
OH
2(aq
aq))
2 (l)
3
3 (aq
aq))
(aq
aq))
(i) Cb
(eq) Cb-x
[CH 3 NH 3+ ] ⋅ [OH − ]
Kb =
[CH 3 NH 2 ]
Cs
Cs+x
nb
nb
Cb − x
Cb
−
V
[OH ] = K b ⋅
≅ Kb ⋅
= Kb ⋅
= Kb ⋅
ns
ns
Cs + x
Cs
V
x
nb
0,1
[OH ] = K b ⋅ = K b ⋅
= Kb
ns
0,1
−
pOH = −log10 [OH ] = −log10 K b = −log10 (4,26 ⋅ 10
−
-4
)
pH = 14 − pOH = 14 + log10 (4,26 ⋅ 10 ) ≅ +10,63
-4
Tipologia di esercizio: Calcolo della variazione di pH di Soluzioni Tampone dopo
aggiunta di piccole o moderate quantità di acido o base forte
Qual è la variazione di pH quando 1,00 mL di una soluzione 1,00 M di HCl
è aggiunto a
1) 1,00 L di acqua pura ;
2) 1,00 L di tampone che ha [CH3COOH] = 0,700 M e [CH3COO−] = 0,600 M
Soluzione della parte 1)
Svolgimento:
Prima dell’aggiunta di HCl il pH di 1,00 L di acqua pura è
2 H 2O
→
←
H 3O + + OH −
K W = [H 3O + ] ⋅ [OH − ] = 1⋅10 −14
[H 3O + ] = 1 ⋅10 −14 = 1 ⋅10 −7 M pH iniziale = −log10 [1⋅10 −7 ] = +7
dopo l'aggiunta di 1,00 mL di HCl 1,00 M a 1,00 L di acqua?
n H O + = n HCl = C HCl ⋅ VHCl = 1 (mol/L ) ⋅ 0,001 L = 0,001 mol
3
0,001 mol 0,001 mol
0,001 mol
mol
[H 3O ] =
=
=
≅ 0,001
Vfinale
VHCl + VH 2O 0,001 L + 1 L
L
+
pH finale = −log10 [1 ⋅10 −3 ] = +3
∆pH = pH iniziale − pH finale = 7 − 3 = 4
Soluzione della parte 2)
Prima dell’aggiunta di HCl il pH di tampone con [CH3COOH] = 0,700 M e
[CH3COO−]=0,600 M è:
CH3COOH(aq) + H2O(l) ⇄ CH3COO-(aq) + H3O+(aq)
(i)
Ca
Cs
Cs+x
(eq) Ca−x
[CH 3COO − ] [H 3O + ] (Cs + x)x
Ka =
=
[CH 3COOH]
(Ca − x)
--x
C a 0,7
0,1 <
=
≅ 1,17 < 10
Cs 0,6
na
Cs [H 3O + ]
C
n
⇒ Ka ≅
⇒ [H 3O + ] ≅ K a a = K a V = K a a
ns
Ca
Cs
ns
V
Ca
-5 0,7
pH = −log10 [H 3O ] = −log10 [K a
] = −log10 [1,8 ⋅10 ⋅
] ≅ + 4,678
Cs
0,6
+
Soluzione della parte 2)
dopo l'aggiunta di 1,00 mL di HCl 1,00 M ?
Ricorda la slide (44) di lezione 19
Parte stechiometria:
H3O+ (da HCl) + CH3COO− (dal tampone) → CH3COOH (dal tampone) + H2O
La reazione avviene completamente (spostata a destra: irreversibile) perché ha
una costante molto grande (è l’inverso della costante acida 1/Ka ≈5,55·10+4).
Ricorda il forte (HCl: acido forte) sposta completamente il debole (CH3COO−: base debole)
Parte stechiometria (più facile ragionare con le moli):
n H O + = n HCl = C HCl ⋅ VHCl = 1 (mol/L ) ⋅ 0,001 L = 0,001 mol
3
n CH COO − = C CH COO − ⋅ Vtampone = 0,600 (mol/L ) ⋅1,0 L = 0,600 mol
3
3
n CH 3COOH = C CH 3COOH ⋅ Vtampone = 0,700 (mol/L ) ⋅1,0 L = 0,700 mol
Moli
H3O+
+ CH3COO−
Iniziali
0,001
0,600
0,700
variazione
-0,001
-0,001
+0,001
Totale fine reazione
0
0,599
0,701
→
CH3COOH
n
Abbiamo ancora un tampone 0,1 < a < 10
ns
na
+
[H 3O ] = K a
Quindi
ns
+ H2O
na
-5 0,701
pH = −log10 [H 3O ] = −log10 [K a ] = −log10 [1,8 ⋅10 ⋅
] ≅ + 4,676
ns
0,599
∆pH = pH iniziale − pH finale = 4,678 − 4,676 = 0,002
+
La variazione di pH è pressoché NULLA c.v.d.
Un paragone scherzoso
Come un tampone (per esempio: CH3COOH/CH3COO−) resiste
alle aggiunte di basi forti (OH−) e acidi forti (H3O+)
È come se
avessimo due
tipi di squali uno
ghiotto di OHe l’altro di H3O+
Purché la popolazione dei
due tipi di squalo
rimanga confrontabile, il
pH tende a rimanere
pressoché costante per
moderate (non
eccessive) aggiunte di
acidi e basi forti.
Tipologia di esercizio: Calcolo della variazione di pH di Soluzioni Tampone dopo
aggiunta di piccole o moderate quantità di acido o base forte
Un tampone viene preparato sciogliendo 2,0 g di acetato di sodio
(CH3COONa) e 1,2 g di acido acetico (CH3COOH, Ka=1,8·10-5 M) in tanta
acqua da avere 200 mL di soluzione. A questa soluzione vengono aggiunti
5,0 mL di una soluzione di NaOH 0,2 M. Si calcoli il pH del sistema prima
e dopo l’aggiunta della base.
Svolgimento:
Prima dell’aggiunta di 5,0 mL NaOH 0,2 M
(i)
(eq)
CH3COOH(aq) + H2O(l) ⇄ CH3COO-(aq) + H3O+(aq)
Ca
Cs
--Ca−x
Cs+x
x
[CH 3COO − ] [H 3O + ] (Cs + x)x
Ka =
=
[CH 3COOH]
(Ca − x)
1,2 g
C a n a n CH 3COOH 60,0520 g/mol 0,01998 mol
0,1 <
=
=
=
=
≅ 0,82 < 10
2,0 g
Cs n s n CH COO −
0,02438 mol
3
82,0338 g/mol n
a
+
C [H O ]
C
n
⇒ Ka ≅ s 3
⇒ [H 3O + ] ≅ K a a = K a V = K a a
ns
Ca
Cs
ns
V
Prima : pH = −log10 [H 3O + ] = −log10 [K a
na
0,01998
] = −log10 [1,8 ⋅10-5 ⋅
] ≅ + 4,83
ns
0,02438
Dopo l’aggiunta di 5,0 mL NaOH 0,2 M
n OH − = n NaOH = C NaOH ⋅ VNaOH = 0,2 (mol/L ) ⋅ 0,005 L = 0,0010 mol
Parte stechiometria:
OH- (da NaOH) + CH3COOH (dal tampone) → CH3COO− (dal tampone) + H2O
La reazione avviene completamente (spostata a destra: irreversibile) perché ha
una costante molto grande (è l’inverso della costante di idrolisi basica
1/Ki=Ka/KW≈1,8·10+9).
Ricorda il forte (NaOH: base forte) sposta completamente il debole (CH3COOH: acido debole)
Moli
OH−
Iniziali
0,00100
0,01998
0,02438
variazione
-0,00100
-0,00100
+0,00100
Totale fine
reazione
0
0,01898
0,02538
+ CH3COOH →
Abbiamo ancora un tampone 0,1 <
na
< 10
ns
+ H2O
na
0,01898
] = −log10 [1,8 ⋅10-5 ⋅
] ≅ + 4,87
ns
0,02538
= 4,83 − 4,87 = 0,04
Dopo : pH = −log10 [H 3O + ] = −log10 [K a
∆pH = pH iniziale − pH finale
CH3COO−
Tipologia di esercizio: Calcolo della variazione di pH di Soluzioni Tampone dopo
aggiunta di piccole o moderate quantità di acido o base forte
Dopo aver calcolato il pH di una soluzione 0,30 M in NH3
(Kb=1,8·10-5 M) e 0,36 M in NH4Cl, calcolare il pH dopo
l'aggiunta di 20,0 mL di una soluzione 0,050 M NaOH a 80,0 mL
di tale soluzione tampone? Svolgimento:
Prima dell’aggiunta di NaOH:
(i)
NH4+(aq)
+
OH
aq)
(aq)
aq)
+
−
[NH
]
⋅
[OH
]
Cs
4
Kb =
[NH 3 ]
x
Cs+x
NH3(
3(aq
aq)) + H2O(l) ⇄
Cb
(eq
eq)) Cb-x
C
0,30 M
0,1 < b =
= 0,83 < 10
Cs 0,36 M
[
Cb −x
Cb
[OH ] = K b ⋅
≅ Kb ⋅
Cs + x
Cs
−
]
0,30 

pOH = −log10 OH − = −log10 1,8 ⋅10 −5 ⋅

0,36 


− 5 0,30 
Prima : pH = 14 − pOH = 14 + log 10 1,8 ⋅10 ⋅
 ≅ +9,176
0,36 

il pH dopo l'aggiunta di 20,0 mL di una soluzione 0,050 M NaOH a 80,0 mL di tale
soluzione tampone?
n OH − = n NaOH = C NaOH ⋅ VNaOH = 0,050 (mol/L ) ⋅ 0,020 L = 0,0010 mol
n NH + = C NH + ⋅ Vtampone = 0,36 (mol/L ) ⋅ 0,080 L = 0,0288 mol
4
4
n NH3 = C NH 3 ⋅ Vtampone = 0,30 (mol/L ) ⋅ 0,080 L = 0,0240 mol
Parte stechiometria:
OH- (da NaOH) + NH4+ (dal tampone) → NH3 (dal tampone) + H2O
La reazione avviene completamente (spostata a destra: irreversibile) perché ha una
costante molto grande (è l’inverso della costante basica 1/Kb ≈5,55·10+4).
Ricorda il forte (NaOH: base forte) sposta completamente il debole (NH4+: acido debole)
Moli
OH−
+ NH4+
Iniziali
0,0010
0,0288
0,0240
variazione
-0,0010
-0,0010
+0,0010
0,0278
0,0250
Totale fine
0
reazione
Abbiamo ancora un tampone
NH3
→
+ H2O
nb
C
n
[OH − ] ≅ K b ⋅ b = K b ⋅ V = K b ⋅ b
ns
Cs
ns
V
nb
< 10
ns
0,025 

Dopo : pH = 14 − pOH = 14 + log 10 1,8 ⋅10 −5 ⋅
 ≅ +9,209
0,0278 

0,1 <
∆pH = pH iniziale − pH finale = 9,176 − 9,209 = 0,033
Tipologia di esercizio: Calcolo della variazione di pH di Soluzioni Tampone dopo
aggiunta di piccole o moderate quantità di acido o base forte
Calcolare la variazione di pH di 1,0 L di una soluzione 0,25 M in NH3
e 0,15 M in NH4Br dopo l'aggiunta di 0,15 mol di HCl. (si consideri nulla la
variazione di volume della soluzione in seguito all’aggiunta di HCl)
Svolgimento:
Prima dell’aggiunta di HCl
(i)
NH4+(aq)
+
OH
aq)
(aq)
aq)
+
−
[NH
]
[OH
]
⋅
Cs
4
Kb =
[NH 3 ]
x
Cs+x
NH3(
3(aq
aq)) + H2O(l) ⇄
Cb
(eq
eq)) Cb−x
0,1 <
C b 0,25 M
=
= 1,667 < 10
Cs 0,15 M
pOH = −log10
[OH − ] = K b ⋅
Cb −x
C
≅ Kb ⋅ b
Cs + x
Cs
[OH ] = −log
−

−5 0,25 
⋅

10 1,8 ⋅10
0,15 


− 5 0,25 
Prima : pH = 14 − pOH = 14 + log 10 1,8 ⋅10 ⋅
 ≅ +9,477
0,15 

il pH dopo l'aggiunta di 0,15 mol di HCl?
n HCl ≡ n H O + = 0,15 mol
3
n NH + = C NH + ⋅ Vtampone = 0,15 (mol/L ) ⋅1,0 L = 0,15 mol
4
4
n NH 3 = C NH 3 ⋅ Vtampone = 0,25 (mol/L ) ⋅1,0 L = 0,25 mol
Parte stechiometria:
H3O+ (da HCl) + NH3 (dal tampone) → NH4+ (dal tampone) + H2O
La reazione avviene completamente (spostata a destra: irreversibile) perché ha una
costante molto grande (è l’inverso della costante di idrolisi acida 1/Ki=Kb/KW≈1,8·10+9).
Ricorda il forte (HCl: acido forte) sposta completamente il debole (NH3: base debole)
Moli
H3O+
+ NH3
Iniziali
0,15
0,25
0,15
variazione
-0,15
-0,15
+0,15
Totale fine reazione
0
0,10
0,30
Abbiamo ancora un tampone
→
NH4+
+ H2O
nb
n
C
n
0,1 < b < 10 [OH − ] ≅ K b ⋅ b = K b ⋅ V = K b ⋅ b
ns
Cs
ns
ns
V
0,10 

Dopo : pH = 14 − pOH = 14 + log 10 1,8 ⋅10 −5 ⋅
 ≅ +8,778
0,30


∆pH = pH iniziale − pH finale = + 9,477 − 8,778 ≅ 0,70
Esercizio di ricapitolazione
Una soluzione 0,240 M di un acido debole (HA) monorprotico ha pH=1,824.
Calcolare:
(a) la costante di dissociazione di HA;
(b) il pH di una soluzione 0,875 M del suo sale NaA;
(c) il pH di una soluzione preparata miscelando 200 mL di una soluzione 0,6 M
di HA con 100 mL di soluzione di NaA 0,3 M.
Svolgimento
(a)
HA(aq)
+ H2O(l)
⇄
H3O+(aq)
+ A-(aq)
Conc. iniziali)
CHA
-
-
Conc. all’eq)
CHA −x
x
x
[H 3O + ] ⋅ [A − ]
x2
Ka =
=
[HA]
C HA − x
e per definizione
pH = - log10 [H 3 O + ] ⇔ [H 3 O + ] = x = 10-pH = 10−1,824 = 0,015 M
x2
(0,015)2
Ka =
=
= 1,0 ⋅10−3 [mol/L]
C HA − x 0,240 − 0,015
(b) Il sale in oggetto NaA, essendo formato dall’anione A di un acido debole
(HA) e dal catione Na+ di una base forte (NaOH), sarà completamente
dissociato in acqua.
[NaA] = [Na + ] = [A − ] = Cs = 0,875 M
L’anione A- dà reazione di idrolisi:
A-(aq)
+ H2O(l)
⇄
HA(aq)
+OH-(aq)
Conc. iniziali)
Cs
-
-
Conc. all’eq)
Cs -x
x
x
[HA] ⋅ [OH - ]
Ki =
[A - ]
K w 1,0 ⋅10-14
-11
Ki = K b =
=
=
1,0
⋅
10
(mol/L) ⇒
-3
K a 1,0 ⋅10
CS
0,875
+10
=
=
8,75
⋅
10
>> 380 ⇒
-11
K i 1,0 ⋅10
[HA] ⋅ [OH - ]
x2
x2
Kb =
=
≅
[A ]
Cs − x Cs
[
x2
⇔ Kb =
⇒ x = K b ⋅ Cs
Cs
]
[
]
⇒ pOH = −log10 OH − = −log10 K b ⋅ Cs = −log10 1,0 ⋅10-11 ⋅ 0,875 = −log10 2,958 ⋅10-6 ≅ 5,53
⇒ pH = 14 − pOH = 14 − 5,53 = 8,47
(c) La soluzione preparata è un tampone:
100 mL di [NaA] = 0,3 M ⇒ n NaA = n A -
200 mL di [HA ] = 0,6 M ⇒ n HA
mol
= 0,3
⋅ 0,100 L = 0,03 mol
L
mol
= 0,6
⋅ 0,200 L = 0,12 mol
L
HA(aq)
+ H2O(l)
⇄
H3O+(aq)
+ A-(aq)
moli iniziali)
0,120
-
0,030
moli all’eq)
0,120-x
x
0,030+x
x (0,030 + x )
⋅
[H 3O ] ⋅ [A ] VT
VT
=
Ka =
(0,120 − x ) ⇔ equazione di 2° grado (VT : volume totale della soluzione)
[HA]
VT
+
−
Tuttavia
n An HA
n A0,03
=
= 0,25 ⇒ 0,1 <
< 10 ⇔ x << 0,12 e 0,03 ⇒ soluzione tampone
0,12
n HA
⇒
[
]
(0,120 - x )
x
n
0,12
VT
 mol 
= H 3O + = K a ⋅
≈ K a ⋅ acido = 1,0 ⋅10 −3 ⋅
= 4,0 ⋅10 −3 

(0,030 + x )
VT
n sale
0,30
 L 
VT
⇒ pH = −log 10[ H 3O + ] = −log 10[4,0 ⋅10 −3 ] ≅ 2,398
Esercizio di ricapitolazione
A quale volume è necessario diluire 30 mL di una soluzione 0,09 M di acido
acetico (CH3COOH, Ka=1.8.10-5) per ottenere una soluzione a pH 3,5. Quale
sarà il nuovo valore di pH se alla soluzione si aggiungono 0,3 g di CH3COONa
(Si consideri nulla la variazione di volume della soluzione in seguito
all’aggiunta del sale).
Svolgimento:
30 mL
C2=?
CH3COOH(aq) + H2O(l) ⇄ CH3COO−(aq) + H3O+(aq)
C1=0,09 M
(i)
C2
----(eq)
C2 – x
x
x
−
+
[CH 3COO ] ⋅ [H 3O ]
Ka =
[CH 3COOH]
x2
Ka =
(C 2 − x)
x = [CH3COO−] = [H3O+] = 10−pH = 10−3, 5
x2
1,8 ⋅10 =
⇒
(C 2 − x)
−5
(C 2 − 10 −3,5 ) ⋅1,8 ⋅10 −5 = 10 −7
⇒
(10 −3,5 ) 2
1,8 ⋅10 =
(C 2 − 10 −3 ,5 )
−5
1,8 ⋅10 −5 C 2 − 1,8 ⋅10 −8,5 = 10 −7
10 −7 + 1,8 ⋅10 −8,5
⇒ C2 =
≅ 0,005872 M
−5
1,8 ⋅10
C1 ⋅ V1 = C 2 ⋅ V2
C1 ⋅ V1 n CH 3COOH 0,09 [mol/L] ⋅ 0,030 [L]
0,0027 [mol]
V2 =
=
=
=
= 0,4598 [L]
C2
C2
0,005872 [mol/L]
0,005872 [mol/L]
Quale sarà il nuovo valore di pH se alla soluzione si aggiungono 0,3 g di CH3COONa?
n CH 3COONa =
m CH 3COONa
PM CH 3COONa
[CH COO ] = C
−
3
S
=
=
0,3 g
= 3,657 ⋅10 −3 mol = n CH COO −
3
82,0338 g/mol
n CH COO −
3
V
3,657 ⋅10 −3 mol
=
0,4598 L
CH3COOH(aq) + H2O(l) ⇄ CH3COO−(aq) + H3O+(aq)
(i)
C2
CS
--(eq)
C2 – x
CS +x
x
Abbiamo un tampone, inoltre : 0,1 < C a = C 2 < 10
CS
CS
(CS + x) ⋅ [H 3O + ] CS [H 3O + ]
≅
Ka =
(Ca − x)
Ca
na
n CH3COOH
Ca
na
2,7 ⋅10 −3
+
−5
V
⇒ [H 3O ] ≅ K a
= Ka
= Ka
= Ka
= 1,8 ⋅10 ⋅
≅ 1,329 ⋅10 −5
−3
nS
CS
nS
n CH COO −
3,657 ⋅10
3
V
⇒ pH = −log 10[H 3O + ] = −log 10 [1,329 ⋅10 −5 ] ≅ 4,876
Esercizio di ricapitolazione
Il pH di una soluzione 0,1 M di un acido debole monoprotico (HA) vale
2,75. Calcolare il numero di moli del sale KA (sale di potassio di A-) che
occorre aggiungere ad un litro di tale soluzione per portare il valore
del pH a 5,00. (Si consideri nulla la variazione di volume della soluzione
in seguito all’aggiunta del sale).
Svolgimento:
I primi dati del problema servono per calcolare la Ka dell’acido debole
HA(aq)
⇄
H3O+(aq)
+ A-(aq)
Conc. iniziali)
CHA
-
-
Conc. all’eq)
CHA −x
x
x
x = [H 3O + ] = [A − ]
e per definizione
+ H2O(l)
[H 3O + ] ⋅ [A − ]
x2
Ka =
=
[HA]
C HA − x
pH = − log10 [H 3 O + ] ⇔ [H 3 O + ] = x = 10− pH = 10−2,75 = 1,778 ⋅10−3 M
x2
(1,778 ⋅10−3 ) 2
−5
Ka =
=
≅
3,22
⋅
10
[mol/L]
−3
C HA − x 0,1 − 1,778 ⋅10
Seconda parte: Il numero di moli del sale KA (sale di potassio di A-) che occorre
aggiungere ad un litro di tale soluzione per portare il valore del pH a 5,00 ?
pH = − log10 [H 3 O + ] ⇔ [H 3 O + ] = x = 1⋅10− pH = 1⋅10−5 M
È chiaro che si forma un tampone per aggiunta di KA (comunque lo
verifichiamo a posteriori)
HA(aq)
Se
nHA
0,1<
<10
nA−
+ H2O(l)
⇄
H3O+(aq)
+ A-(aq)
Moli iniziali)
nHA
-
nA-
Moli all’eq)
nHA−x
x
nA+x
abbiamo un tampone
⇒ [H 3O + ] ≅ K a
n HA
n A−
n HA = C HA ⋅ Vsoluzione = 0,1(mol/L ) ⋅1,0 L = 0,1 mol
0,1
1 ⋅10 = 3,22 ⋅10 ⋅
n A−
−5
−5
Si verifica che
n A−
0,1
= 3,22 ⋅10 ⋅
= 0,322 [mol]
−5
1⋅10
nHA
0,1 <
<10
nA−
−5
Esercizio di ricapitolazione
In una soluzione di 100 mL di acido cloridrico (HCl) ha pH 2,31, si fanno
assorbire 25 mL misurati a c.n. di ammoniaca gassosa, calcolare il pH finale
della soluzione sapendo che Kb=1,8.10-5 M. (Assumere che il volume della
soluzione resti invariato in seguito all’assorbimento del gas).
Risoluzione:
100 mL di acido cloridrico (HCl) con pH 2,31:
⇒ [H 3O + ] = 10 − pH = C HCl = 10 −2,31 ≅ 4,898 ⋅10 −3 M ⇒
n H O + = [H 3O + ] ⋅ VHCl = 4,898 ⋅10 −3 M ⋅ 0,100 L = 4,898 ⋅10 − 4 mol
3
+ 25 mL misurati a c.n. di ammoniaca gassosa
V
mL
⇒ Vm = = 22414
n
mol
⇒ n NH 3 =
VNH 3
Vm
=
25 mL
≅ 11,15 ⋅10 − 4 mol
mL
22414
mol
H3O+(aq) + NH3(aq) → NH4+(aq) + H2O(aq)
MOLI
I)
4,898 ⋅10
−4
−4
Δ) − 4,898 ⋅10
TOTALE)
−−−
−−−
−−−
− 4,898 ⋅10 −4
+ 4,898 ⋅10 −4
+ 4,898 ⋅10 −4
6,252 ⋅10 −4
4,898 ⋅10 −4
11,15 ⋅10
−4
Ho la
formazione di un
tampone
ammoniaca/ione
ammonio
NH4+(aq
+
OH
aq))
(aq
aq))
NH3(aq
3(aq)) + H2O(l)
(i) Cb
(eq) Cb−x
Cs
Cs+x
x
[NH +4 ] ⋅ [OH − ]
Kb =
[NH 4 ]
nb
Cb −x
Cb
nb
−
V
[OH ] = K b ⋅
≅ Kb ⋅
= Kb ⋅
= Kb ⋅
ns
Cs + x
Cs
ns
V
−4
n NH3
n NH3
nb
6,252 ⋅10
−5 6,252
[OH ] = K b ⋅
= Kb ⋅
= Kb ⋅
= 1,8 ⋅10 −5 ⋅
=
1
,
8
⋅
10
⋅
−4
nS
n NH +
n NH +
4,898 ⋅10
4,898
−
4
4
[
]
6,252 

pOH = −log10 OH − = −log10 1,8 ⋅10 −5 ⋅

4,898 


−5 6,252 
pH = 14 − pOH = 14 + log 10 1,8 ⋅10 ⋅
 ≅ +9,36
4,898 

Degli ottimi Esercizi riassuntivi e integrativi
sono i seguenti:
Ricorda che hai bisogno di una
calcolatrice scientifica per
calcolare il pH
+
pH = −log 10 [H 3O ]
Esercizi riassuntivi e integrativi
1) Si prepara un sistema tampone mescolando 184,0 mL di una soluzione acquosa
0,442 M di acido cloridrico (HCl) con 0,50 L di una soluzione acquosa 0,400 M di
acetato di sodio (CH3COONa). Si calcoli la massa in grammi di idrossido di potassio
(KOH) che deve essere aggiunta a 100,0 mL di tale tampone per farne variare il pH
di 0,15 unità. (Per l’acido acetico (CH3COOH) pKa=4,75) [0,130 g]
2) Si abbiano, alla temperatura di 25,0°C, 250,0 mL di una soluzione acquosa
contenente, contemporaneamente, 2,35 g di HNO2 e 1,72 g di NaNO2. A questa
soluzione si aggiungano 10,0 mL di una soluzione 0,10 M di HCl. Si calcoli il pH del
sistema prima e dopo l'aggiunta dell'acido forte (per HNO2, Ka = 4,0 ·10−4 M).
[pH iniziale: 3,10, pH finale: 3,07]
3) Una soluzione acquosa 0,10 M del sale sodico, NaA, dell'acido debole HA
presenta, a 25,0°C, un valore di pH pari a 11,30. Si calcoli, sempre a 25,0°, il valore
del pH assunto dal sistema ottenuto aggiungendo a 100,0 mL della soluzione del sale
40,0 mL di una soluzione 0,25 M di HCl. Si considerino i volumi additivi.
[pH=5,38]
4) Una soluzione acquosa 0,10 M di un acido debole monoprotico presenta, a 298,0 K,
pH = 3,15. A 2,50 L di tale soluzione vengono aggiunti 24,0 mL di una soluzione
acquosa di NaOH (7,50% in peso; d = 1,015g/mL). Considerando i volumi additivi,
calcolare il pH della soluzione. [pH =4,65]
Esercizi riassuntivi e integrativi
5) A 100,0 mL di una soluzione acquosa 0,10 M del sale di sodio, NaA, dell'acido
debole monoprotico HA (per HA: Ka = 1,0·10−5 M) vengono aggiunte due porzioni
successive, da 25,0 mL l'una, di una soluzione acquosa 0,20 M di HCl. Considerando
i volumi additivi, si calcoli il pH del sistema prima dell'aggiunta dell'acido cloridrico
e dopo ciascuna delle due aggiunte; si tenga presente che tutte le operazioni vengono
condotte alla temperatura T= 298,0 K. [All’inizio: pH = 9,00; dopo la prima
aggiunta: pH = 5,00 ; dopo la seconda aggiunta: pH = 3,09]
6) Alla temperatura di 298,0 K, a 50,0 mL di una soluzione acquosa 0,1 M di acido
nitroso (Ka = 4,0·10−4M) vengono aggiunte due porzioni, ciascuna da 12,5 mL, di una
soluzione acquosa 0,20 M di idrossido di sodio. Considerando i volumi additivi,
calcolare il pH del sistema prima dell'aggiunta della base e dopo ciascuna delle due
aggiunte. [pH iniziale: 2,21; pH dopo la prima aggiunta: 3,40; pH dopo la seconda
aggiunta: 8,11]
7) Una soluzione acquosa 0,10 M di cianuro di potassio, KCN, presenta, a 298,0 K,
pH = 10,95. Si calcoli, alla stessa temperatura, il pH presentato da una soluzione
acquosa 0,20 M di acido cianidrico, HCN. [pH = 4,80]
8) Una soluzione acquosa 0,10 M di cloruro di ammonio, NH4Cl, presenta, a 298,0 K,
pH = 5,13. Si calcoli, alla stessa temperatura, il pH presentato da una soluzione acquosa
0,20 M di ammoniaca, NH3. [pH =11,28]
Esercizi riassuntivi e integrativi
9) Alla temperatura di 298,0 K, si è in possesso delle seguenti due soluzioni:
(a) 100 mL di un acido debole HA (Ka = 1·10−4 M) di concentrazione 0,1 M;
(b) 100 mL di idrossido di potassio di concentrazione 0,20 M;
Considerando i volumi additivi, indicare quale volume della soluzione b) deve essere
aggiunto a 50 mL della soluzione a) per ottenere un sistema finale il cui pH valga 4,00
[V = 12,5 mL]
10) Si abbiano, alla temperatura di 25,0°C, 300,0 mL di una soluzione acquosa
contenente, contemporaneamente, 1,18g dell'acido debole monoprotico HA
(PMHA=47,0 dalton) e 3,45g del suo sale di sodio. A questa soluzione si aggiungano
10,0 mL di una soluzione 1,0 M di HCl. Si calcoli il pH del sistema prima e dopo
l'aggiunta dell'acido forte (si considerino i volumi additivi; per HA, Ka = 4,5·10−4 M).
[pH prima dell’aggiunta: 3,65; pH dopo l’aggiunta: 3,40]
11) Una soluzione acquosa di KOH presenta un pH pari a 13,18. 230,0 mL di questa
soluzione vengono aggiunti a 402,0 mL di una soluzione acquosa 0, 13M di cloruro di
ammonio. Si calcoli il valore assunto dal pH del sistema dopo il mescolamento delle
due soluzioni (considerare i volumi additivi; T = 298,0 K; per NH3: Kb=1,8·10−5)
[pH = 9,56]
Esercizi riassuntivi e integrativi
12) A 25,0°C , il pH di una soluzione acquosa 0,100M di acido fluoridrico (HF) è
pari a 2,24. Si calcoli, alla stessa temperatura, il valore del pH di una soluzione
acquosa 0,400 M di fluoruro di sodio NaF. [pH = 8,53]
13) Calcolare la variazione di pH che si ha in 2,00L di una soluzione contenente
contemporaneamente NaBrO2 (0,40M) e HBrO2 (0,50 M) per l’aggiunta di 10,00 g
di NaOH. (a T = 298 K; l’aggiunta dell’idrossido di sodio non causa variazioni nel
volume della soluzione; per l’acido bromoso, HBrO2, Ka= 2,04·10−6 M).
[pH iniziale: 5,59; pH finale: 5,84; ∆pH = 0,25]
14) Si abbiano, alla temperatura di 25,0°C, 250,0 mL di una soluzione acquosa
contenente, contemporaneamente, 1,72g di HClO2 e 5,33g di KClO2. A questa
soluzione si aggiungano 10,0 mL di una soluzione 1,0 M di NaOH. Si calcoli il pH
del sistema prima e dopo I'aggiunta della base forte (si considerino i volumi additivi;
per HClO2, Ka = 6,5 ·1 0−4 M) [pH iniziale: 3,49; pH finale: 3,78]
15) A 25,0°C, il pH di una soluzione acquosa 0,100 M di nitrito di potassio (KNO2)
è pari a 8,17. Si calcoli, alla stessa temperatura, il valore del pH di una soluzione
acquosa 0,250 M di acido nitroso (HNO2). [pH = 1,98]
Esercizi riassuntivi e integrativi
16) Una soluzione acquosa di HCl presenta un pH pari a 1,20. 115,0 mL di questa
soluzione vengono aggiunti a 90,0 mL di una soluzione acquosa 0,13 M di acetato di
sodio (CH3COONa). Si calcoli il valore assunto dal pH del sistema dopo il
mescolamento delle due soluzioni (considerare i volumi additivi; T = 298,0 K; per
CH3COOH, Ka=1,8·10-5 M). [pH = 4,53]
17) Alla temperatura di 25,0°C , a 100,0 mL di una soluzione acquosa 0,100 M di un
acido debole monoprotico vengono aggiunti 40,0 mL di una soluzione 0, 150 M di
idrossido di sodio. Calcolare il valore del pH della soluzione risultante, sapendo che,
per l’acido debole, Ka = 4,60·10−4 M. Si considerino i volumi additivi. [pH = 3,51]
18) La soluzione 0,10 M dell’acido debole monoprotico HA presenta, alla temperatura
di 298,0 K, un valore del pH pari a 2,65. Considerando i volumi additivi, calcolare il
volume di acqua che occorre aggiungere a 10,0 mL di tale soluzione perché il pH
assuma il valore di 3,50. [V = 431,2 mL di acqua]
19) 100,0 mL di una soluzione 6,25·10-2 M dell'acido monoprotico debole HA
(Ka=1,541·10−5 M) vengono aggiunte, a 25,0°C, due porzioni, ciascuna da 25,0 mL,
di una soluzione 0, 125M di idrossido di sodio. Considerando i volumi additivi, si
calcoli il pH del sistema prima e dopo l’aggiunta di ciascuna porzione della
soluzione basica. [pH1 = 3,02; pH2 = 4,84; pH3=8,73]
Esercizi riassuntivi e integrativi
20) A 100,0 mL di una soluzione acquosa di concentrazione 5,011·10−2 M dell'acido
monoprotico debole HA vengono aggiunti 100,2 mg di idrossido di sodio solido,
senza che si verifichino variazioni di volume. In tali condizioni, il sistema presenta, a
25,0°C, un valore del pH pari a 3,67. Si calcoli il valore del pH della soluzione
iniziale dell'acido. [pH = 2,50]
21) Una soluzione acquosa di concentrazione 6,227·10−2 M dell'acido monoprotico
debole HA presenta, a 25,0°C, un valore del pH pari a 2,94. A 50,0 mL di tale
soluzione vengono aggiunti 70,3 mg di idrossido di potassio solido, senza che si
verifichino variazioni di volume. Si calcoli il valore del pH del sistema in queste ultime
condizioni. [pH = 4,49]
22) A 100,0 mL di una soluzione acquosa 0,10 M del sale di potassio, KA, dell'acido
debole monoprotico HA (per HA: Ka = 5,0·10-6 M) vengono aggiunte due porzioni
successive, da 20,0 mL l’una, di una soluzione acquosa 0,25 M di HCl. Si calcoli il pH
del sistema prima dell'aggiunta dell'acido cloridrico e dopo ciascuna delle due
aggiunte, tenendo presente che tutte le operazioni vengono condotte alla temperatura T
= 298,0 K e considerando i volumi additivi. [pH1=9,15; pH3=5,30; pH3=3,22]
Esercizi riassuntivi e integrativi
23) Una soluzione acquosa di idrossido di sodio (NaOH) presenta, alla temperatura di
25,0°C, pH=10,50. Si calcoli la quantità in peso di acido acetico (CH3COOH) che è
necessario aggiungere a 125,0 mL di tale soluzione affinché il pH assuma il valore di
5,00. Si consideri invariato il volume del sistema dopo l'aggiunta dell'acido; per
l’acido acetico Ka=1,8·10−5 M. [3,68 mg]
24) A 1,00 L di una soluzione acquosa contenente contemporaneamente 0,10 mol di
NH3 e 0,100 mol di NH4Cl vengono aggiunte 10,0 mmol di HCl (il volume della
soluzione resta invariato). Calcolare il pH del sistema tampone prima e dopo
l’aggiunta dell’acido (Per NH3, Kb = 1,8·10−5 M; T = 298,0 K) [Prima pH=9,26;
dopo pH=9,17]
25) Alla temperatura di 298,0 K, una soluzione 0,20 M dell’acido HA presenta un
valore del pH pari a 2,40. A 15,0 mL di tale soluzione si aggiunge acqua fino ad avere
un volume finale pari a 350,0 mL. Si calcoli il valore del pH della soluzione diluita
dell'acido HA. [pH = 3,10]
Esercizi riassuntivi e integrativi
26) Calcolare il pH di una soluzione 0,001 M di idrogenosolfato di potassio
(KHSO4). La costante della seconda reazione di trasferimento protonico di H2SO4
vale Ka=1,2·10−2 M. [pH=3,03]
27) 200 mL di una soluzione di HCl 5,0 M vengono addizionati a 130 mL di una
soluzione di NH3 (Kb=1,8·10−5 M) al 32% in peso, d=0,89 g/mL. Si calcoli il pH del
sistema dopo il mescolamento. [pH=9,33]
28) Calcolare il volume di una soluzione 0,2M di NaOH che bisogna aggiungere a
100 mL di una soluzione 0,1 M di un acido debole monoprotico (Ka =2,6·10−5 M)
per ottenere una soluzione a pH =5,8. [V=47,1 mL]
29) Il pH di una soluzione 0,2 M di cianuro di potassio (KCN) è pari a 11,30.
Calcolare il volume di una soluzione concentrata di acido perclorico (HClO4, d=1,67
g/mL; 69,5% in peso) che bisogna aggiungere a 100 mL della soluzione di partenza
per portarne il pH al valore di 9,60. [V=0,58 mL]
Esercizi riassuntivi e integrativi
30) A 25,0 mL di una soluzione 0,2 M di un acido debole HA (pH = 2,78) vengono
aggiunte due porzioni successive, ciascuna da 25,0 mL, di una soluzione 0,1 M di
KOH. Si determini il valore del pH dopo ogni aggiunta della soluzione di base.
[pH=4,86; pH=8,84]
31) Si dispone di una soluzione di NH3 (Kb =1,8·10-5 M) di pH pari a 11,28 e di una
soluzione di HCl di pH=1,00. Si determini il rapporto dei volumi delle due soluzioni,
perché, una volta mescolatele, il sistema assuma pH =9,5. [VNH3 /VHCl=1,378]
32) 500 mL di una soluzione 0,2 M di un acido debole monoprotico HA vengono
addizionati di 800 mL di una soluzione 0,03 M di NaOH; il pH della soluzione
risultante è pari a 2,80. Si calcoli il valore della costante di dissociazione, Ka,
dell'acido debole. [Ka=5,00·10-4 M]
33) Mescolando campioni di stesso volume di soluzioni di pari concentrazione
(0,001 M) di un acido debole monoprotico HA e di idrossido di potassio si ottiene un
sistema il cui pH è pari a 8,70. Si calcolino: (a) la costante di dissociazione, Ka, di
HA; (b) il pH della soluzione iniziale di HA. [Ka = 1,97·10-7 M, pH=4,85]
34) Calcolare a quale volume occorre diluire 100 mL di una soluzione 0,1 M di
CH3COOH per ottenere una soluzione avente pH = 3,5. Calcolare inoltre la % in peso
di una soluzione di KOH (densità = 1,15 g/mL), sapendo che se ne devono usare 20
mL per portare il pH della soluzione di acido acetico, dopo la diluizione, a 6,3.
[Vdiluzione=1,8 L; %W KOH=2,37]
Esercizi riassuntivi e integrativi
35) I vari tipi di candeggina altro non sono che soluzioni diluite (all’incirca al 5%
in peso) di ipoclorito di sodio (NaClO). Qual è il pH di una soluzione di tale
candeggiante che contenga ipoclorito di sodio in quantità pari a 50,0 g/L? La
costante di dissociazione (Ka) dell’acido ipocloroso (HClO) è 3,1·10-8 M. [10,67]
36) Una soluzione di acetato di sodio (CH3COONa) ha pH=9,00. Calcolare quanta
acqua bisogna aggiungere a 0,5 litri di questa soluzione affinché il pH diventi
uguale ad 8,00. Per l’acido acetico (CH3COOH), Ka = 1,8·10−5 M.
[V H2O=49,5 L]
Chimica
(a.a. 2010/2011, 6CFU)
Equilibri ionici in soluzione acquosa (IV parte):
Equilibri di solubilità
Esercitazione
Esercizi integrativi
EQUILIBRI DI SOLUBILIT
SOLUBILITÀ
À
Alcuni elettroliti forti (cioè quelli che si dissociano
completamente in ioni) sono molto solubili:
NaCl(s) → Na+(aq) + Cl-(aq)
KOH(s) → K+(aq
+
OH
(aq
aq))
aq))
Alcuni elettroliti forti sono poco solubili:
AgCl(s) ⇄ Ag+(aq) + Cl-(aq
aq))
CaCO3(s) ⇄ Ca2+(aq) + CO32-(aq
aq))
Ni(OH)2(s) ⇄ Ni2+(aq) + 2 OH-(aq
aq))
3Ca3(PO4)2(s) ⇄ 3 Ca2+(aq
aq)) + 2 PO4 (aq
aq))
dando origine a soluzioni sature o sovrasature ove si
stabiliscono gli equilibri sopra riportati.
Esempio di soluzione satura
Si stabilisce l’equilibrio eterogeneo [solidoliquido (soluzione)]:
Ca(OH)2(s) ⇄ Ca2+(aq
+
2
OH
aq))
(aq
aq))
Ca2+(aq) + 2 OH-(aq)
Ca(OH)2(s)
All’equilibrio corrisponde una costante di equilibrio:
K=
2
a Ca 2+ ⋅ a OH
−
a Ca(OH)2
che assumendo comportamento ideale della soluzione
e attività unitaria per il solido diventa:
2+
− 2
K = [Ca ] ⋅ [OH ]
–6
3
K = 4,68 · 10 M
Visibile il corpo di fondo (il solido:
idrossido di calcio) della soluzione
Molti composti ionici sono, quindi, poco solubili o
praticamente insolubili e instaurano un equilibrio con gli
ioni costituenti nella soluzione satura.
Ad esempio per il cloruro di argento si ha:
AgCl(s)
Ag+(aq) + Cl-(aq)
cui corrisponde (ad
ad un data temperatura)
temperatura una costante di equilibrio Ks, detta
prodotto di solubilità:
+
È una costante di un equilibrio eterogeneo
dove assegniamo attività unitaria al solido
−
K s = [Ag ] ⋅ [Cl ]
(KS è anche indicata come
KPS o come KSP
(testi americani) e raramente come PS)
Altri esempi di sali poco solubili sono:
PbI2(s)
Ca3(PO4)2(s)
Pb2+(aq) + 2I-(aq)
K s = [Pb 2+ ] ⋅ [I − ]2 = 8,49 · 10 –9 M 3
3 Ca2+(aq) + 2 PO43-(aq)
2+ 3
3− 2
4
K s = [Ca ] ⋅ [PO ] = 2,07 · 10
–33
M
5
REGOLE QUALITATIVE DI SOLUBILITA’
NITRATI ED ACETATI di tutti i metalli sono SOLUBILI in
acqua. L’Ag acetato è poco solubile.
Tutti i Sali d’AMMONIO, POTASSIO e SODIO sono SOLUBILI
in acqua.
CLORURI, BROMURI e IODURI di tutti i metalli, ESCLUSO
PIOMBO, ARGENTO E MERCURIO(I), sono SOLUBILI in acqua. Lo
ioduro di mercurio(II), HgI2, è INSOLUBILE in acqua, mentre
PbCl2, PbBr2 e PbI2 diventano solubili in acqua molto calda. I
cloruri, bromuri e ioduri insolubili in acqua sono insolubili anche in
ACIDI diluiti.
i SOLFATI di tutti i metalli, ESCLUSO PIOMBO, BARIO,
CALCIO E MERCURIO(I), sono SOLUBILI in acqua. Il solfato di Ag
è poco solubile. I solfati insolubili in acqua sono insolubili anche in
ACIDI diluiti.
REGOLE QUALITATIVE DI SOLUBILITA’
CARBONATI, FOSFATI, BORATI, CROMATI ed ARSENIATI di
tutti i metalli, escluso sodio, potassio ed ammonio, sono
INSOLUBILI in acqua ma solubili in ACIDI diluiti.
i SOLFURI di tutti i metalli, escluso magnesio, bario, calcio,
sodio, ammonio e potassio, sono INSOLUBILI in acqua. BaS, CaS e
MgS sono moderatamente solubili.
IDROSSIDI di sodio, potassio e ammonio sono MOLTO SOLUBILI
in acqua. Gli IDROSSIDI di calcio e bario sono moderatamente
solubili. Ossidi e idrossidi di tutti gli altri metalli sono insolubili.
Per calcoli quantitativi dobbiamo usare
valori KS (prodotti di
solubilità) che generalmente sono tabulati ad una certa temperatura
(di solito quella standard 25°
25°C)
Per esempio nel libro Nobile-Mastrorilli trovate:.
TABELLA 15.3
Prodotti di
solubilità
dei principali sali
insolubili.
Altri esempi di sali poco solubili sono:
2CaCO3(s) ⇄ Ca2+(aq
+
CO
aq))
3 (aq
aq))
2+
2−
3
K s = [Ca ] [CO ]
a 25°C KS = 4,96 · 10–9 M2
2Ag2CO3(s) ⇄ 2 Ag+(aq
+
CO
aq))
3 (aq
aq))
+ 2
2−
3
K s = [Ag ] [CO ]
a 25°C KS = 8,45×10-12 M2
Fe(OH)3(s) ⇄ Fe3+(aq
aq)) + 3 OH (aq
aq))
3+
− 3
K s = [Fe ] [OH ]
a 25°C KS = 2,64 · 10–39 M4
Si intende con
solubilità il numero
di moli di sale che si sciolgono
per litro di soluzione.
Essa è indicata con s ed è legata alle concentrazione dei vari ioni in cui si
dissocia il sale dai coefficienti stechiometrici.
Solubilità = concentrazione (molare:
Solubilità
(molare: mol·
mol· L-1) del soluto che si scioglie nella
soluzione, all’equilibrio, ad una certa temperatura.
temperatura.
Solubilità
Solubilit
à (S, in mol
mol·· L-1) in acqua pura:
Ag2CO3(s) ⇄ 2 Ag+(aq) + CO32-(aq)
2S
S
K S = 8,45 ⋅10 −12 M 3 = [Ag + ]2 ⋅ [CO 32− ] = (2S) 2 ⋅ S = 4S3
S=3
−12
Ks
8,45
⋅
10
=3
= 1,283 ⋅10 − 4 M
4
4
a 25°C
Un altro esempio
Solubilità
Solubilit
à ((S
S, in mol·
mol· L-1) in acqua pura del carbonato di calcio:
CaCO3(s) ⇄ Ca2+(aq) + CO32-(aq)
S
S
2+
2−
3
−9
K S = [Ca ] ⋅ [CO ] = 4,96 ⋅10 [M ] = S
S = K S = 4,96 ⋅10
−9
2
−5
= 7,04 ⋅10 M
a 25°C
2
Un altro esempio
Solubilità
Solubilit
à (s, in mol
mol·· L-1) in acqua pura del carbonato di calcio:
Fe(OH)3(s) ⇄ Fe3+(aq) + 3 OH-(aq)
S
3S
KS=[Fe3+]·[OH-]3=2,64·10−39 M4
Solubilità a 25°C
in acqua pura:
K S = S ⋅ (3S) 3 = 27S4
−39
K
2,64
·10
S=4 S =4
= 9,94 ⋅10 −11 M
27
27
Solubilità a 25°C in
soluzione acida tamponata a
pH=4, cioè pOH=10 e
quindi [OH-]=10-10 M:
(
K S = S ⋅ (10 −10 ) 3 = S ⋅ 1 ⋅10 −30
)
KS
2,64 ⋅10 −39
−9
S=
=
=
2
,
64
⋅
1
0
M
−30
−30
1 ⋅10
1 ⋅10
Generalizzando
Per il generico elettrolita (sale) AaBb poco solubile, per ogni sua mole che si
dissocia in a mol di cationi Ab+ e in b mol di anioni Ba- abbiamo che :
A a Bb (s)
aA
b+
(aq)
+bB
a−
(aq)
Concentraz. iniziali
(Δ) Variaz. concentraz.
---
-+aS
-+bS
Concentraz. Equilibrio
--
aS
bS
S = solubilità molare (mol/L) di AaBb
b+ a
a− b
K s = [A ] ⋅ [B ] = (aS) ⋅ (bS)
a
Dato tabulato (false dimensioni: Ma+b) a
una certa temperatura (generalmente
quella standard: 298,15 k)
b
 mol  a + b K s
S
=
b
a

b ⋅a
 L 
Esercizio: Calcolo del Ks dalla solubilità – Calcolare il KS del PbI2
sapendo che la sua solubilità è di 1,285·10−3 mol/L.
−
PbI2(s) ⇄ Pb2+(aq
aq)) + 2 I (aq
aq))
Concentraz. iniziali
Variaz. concentraz.
Concentraz. Equilibrio
-
0
+S
S
0
+2 S
2 S
KS=[Pb2+]·[I-]2
[Pb2+]=S [I-]=2S
KS=[Pb2+]·[I-]2=S·(2S)2=4S3 KS=4S3 =4(1,285·10-3)3= 8,49·10-9 M3
Esercizio: Calcolo della solubilità dal KS – Calcolare la solubilità
dell’AgCl sapendo che il suo Ks vale 1,77·10-10M
−
AgCl(s) ⇄ Ag+(aq
+
Cl
aq))
(aq
aq))
Concentraz. iniziali
Variaz. concentraz.
Concentraz. Equilibrio
-
KS=[Ag+]·[Cl-]= 1,77·10-10 M2=S⋅⋅S=S2
S = K S = 1,77 ⋅10 -10 = 1,33 ⋅10 -5 M
0
+S
S
0
+S
S
S = KS
solubilità = 1,33 ⋅10 −5 M
Calcolo della solubilità dal Ks (un altro esempio)
Calcolare la solubilità del CaF2 sapendo che il suo Ks vale 1,46·10-10
M3.
CaF2(s) ⇄ Ca2+(aq) +2 F-(aq)
Concentraz. iniziali
Variaz. concentraz.
Concentraz. Equilibrio
-
0
+S
S
K S = [Ca 2+ ] ⋅ [F − ]2 = S·(2S)2 = 4S3 = 1,46 ⋅10 −10 M 3
Ks
S=
4
3
−10
K
1
,
46
⋅
10
S=3 s =3
≅ 3,32 ⋅10 −4 M
4
4
0
+2S
2S
EFFETTO DELLO IONE COMUNE
Consideriamo ora la solubilità di un sale poco solubile in una soluzione
contenente uno dei due ioni implicati nell’equilibrio di solubilità, ad
esempio, di PbI2(s) in una soluzione di NaI:
In base al principio di Le Chatelier, l’equilibrio viene spostato verso sinistra dalla
presenza di I- per cui possiamo prevedere che la solubilità in NaI sia inferiore a
quella dell’acqua pura.
Calcoliamo ad esempio la solubilità di AgBr, per il quale KS=5,56×10-13 M2 in una
soluzione di NaBr 0,10 M.
In soluzione l’NaBr (elettrolita forte) è dissociato completamente
NaBr(s) → Na+(aq) + Br-(aq)
per cui la soluzione è 0,10 M in Br- che uno ione in comune con l’ AgBr:
Le concentrazioni all’equilibrio vanno calcolate da:
AgBr(s)
Concentraz. iniziali
Variaz. concentraz.
Concentraz. Equilibrio
-
Ag+(aq) + Br-(aq)
0
+S
S
0,10
+S
0,10+S
K S = 5,56 ⋅10 −13 = [Ag + ]·[Br − ] = S·(0,10 + S)
Si noti che S è molto piccola per cui 0,10+S≈0,10
K S = S ⋅ 0,10
KS
5,56 ⋅10 −13
S=
=
= 5,8 ⋅10 −12 M
0,10
0,10
Si noti come la solubilità è inferiore a quella in acqua pura:
S = K S = 5,56 ⋅10 −13 = 7,46 ⋅10−7 M
EFFETTO DELLO IONE COMUNE
MgF2(s) ⇄ Mg2+(aq) +2 F-(aq)
K S = [Mg 2+ ] ⋅ [F − ]2 = S·(2S)2 = 4S3 = 7,42 ⋅10 −11 M 3
−11
K
7
,
42
⋅
10
S=3 s =3
≅ 2,65 ⋅10 − 4 M
4
4
Se aggiungo NaF la
solubilità a mano a mano
diminuisce ……
Per esempio [F-]=0,040 M
K S = [Mg 2+ ] ⋅ [F − ]2 =
S·(2S + 0,040) 2 ≅ S·(0,040)2 =
= 7,42 ⋅10 −11 M 3
KS
7,42 ⋅10 −11
S=
=
=
2
0,10
(0,040)
= 4,6375 ⋅10 −8 M
in acqua pura
EFFETTO DELLO IONE COMUNE
Soluzione
sovrassatura di AgCl
Soluzione
sovrassatura di AgCl
dove è stata aggiunta una
aliquota di una soluzione di
nitrato di argento (AgNO3
sale solubile di argento:
AgNO3 → Ag+ +NO3- )
La quantità di
precipitato aumenta
Precipitazione
Consideriamo due soluzioni di sali solubili contenenti ciascuna uno dei
due ioni che partecipano ad un equilibrio di solubilità di un sale poco
solubile.
Prendiamo ad esempio una soluzione di AgNO3 (che è solubile e
dissocia negli ioni Ag+ e NO3-) ed una di NaCl (che è solubile e
dissocia negli ioni Na+ e Cl- ): se le mescoliamo abbiamo nella
soluzione risultante la presenza degli ioni Ag+ e Cl – che partecipano
all’equilibrio di solubilità:
AgCl(s) ⇄ Ag+(aq) + Cl−(aq)
Se le concentrazioni [Ag+] e [Cl –] subito dopo il mescolamento sono
sufficientemente elevate si ha formazione immediata nel corpo della
soluzione di AgCl solido: la soluzione diventa improvvisamente torbida
per la presenza di particelle di AgCl in sospensione e solo dopo un
certo tempo il solido si deposita sul fondo lasciando in soluzione
concentrazioni [Ag+] e [Cl –] compatibili con l’equilibrio.
Tale fenomeno è noto come precipitazione
precipitazione.
Formazione di precipitati (Precipitazione
Precipitazione))
NaCl(s) → Na+(aq) + Cl-(aq)
Na+(aq)
Cl-(aq)
AgNO3(s) → Ag+(aq) + NO3-(aq)
AgCl(s) ⇄ Ag+(aq) + Cl-(aq)
Ks =1,77·10-10 M
Ag+(aq)
NO3-(aq)
Na+(aq)
Cl-(aq)
Ag+(aq)
NO3-(aq)
Na+(aq)
Cl-(aq)
Ag+(aq)
NO3-(aq)
AgCl((s) ⇄ Ag+(aq) + Cl-(aq)
AgCl
Esempio: aggiunta di una soluzione di NaCl ad una di AgNO3
NaCl
AgNO3
AgCl
NaCl(aq) + AgNO3(aq) → AgCl(s) + NaNO3(aq)
In forma ionica:
Ag+(aq
+
Cl
aq))
(aq
aq)) → AgCl(s)
Altro esempio: aggiunta di una soluzione di K2CrO4 ad una di Pb(NO3)2
Pb(NO3)2
K2CrO4
PbCrO4
Altro esempio: aggiunta di una soluzione di K2CrO4 ad una di Pb(NO3)2
K2CrO4 (aq) + Pb(NO3)2(aq) → PbCrO4 (s) + 2 KNO3 (aq)
In forma ionica:
2Pb2+(aq
+
CrO
aq))
4 (aq
aq)) → PbCrO4(s)
(s)
Altro esempio: aggiunta di una soluzione di Pb(NO3)2 ad una di NaI
Pb(NO3)2
NaI
PbI2
Altro esempio: aggiunta di una soluzione di Pb(NO3)2 ad una di NaI
2 NaI (aq) + Pb(NO3)2(aq) → PbI2 (s) + 2 NaNO3 (aq)
In forma ionica:
Pb2+(aq
+
2
I
aq))
(aq
aq)) → PbI2(s)
(s)
Per determinare se si ha o no precipitazione in seguito al mescolamento
delle due soluzioni, si fa uso del criterio generale per determinare in che
direzione procede una reazione per raggiungere l’equilibrio a partire da
concentrazioni iniziali note di reagenti e prodotti:
Se
QS > KS
la reazione procede verso sinistra
Se
QS < KS
la reazione procede verso destra
Se
QS = KS
la reazione è all’equilibrio
QS corrisponde ad un prodotto ionico che ha la stessa espressione del KS,
tuttavia le concentrazioni dei due ioni non sono quelle all’equilibrio ma
quelle della soluzione subito dopo il dal mescolamento. Ad esempio per la
solubilità di AgCl:
KS= [Ag+]eq[Cl-]eq
QS = [Ag+]0[Cl-]0
Questa situazione corrisponde a mescolare i due prodotti della
reazione di equilibrio di solubilità e determinare in che direzione si
sposta la reazione per raggiungere l’equilibrio.
Ad esempio per l’equilibrio di solubilità:
AgCl(s) ⇄ Ag+(aq) + Cl-(aq)
poiché solo uno spostamento a sinistra di tale reazione corrisponde
alla formazione di AgCl(s) cioè alla precipitazione, si deriva
immediatamente il seguente criterio:
Se
QS > KS
si ha precipitazione
Se
QS ≤ KS
non si ha precipitazione
Le concentrazioni da inserire in QS sono quelle dopo il mescolamento e
si ottengono a partire da quelle delle due soluzioni mescolate tenendo
conto della diluizione.
diluizione.
Esempio – Se mescoliamo 1,0 litri di una soluzione 0,10 M di Pb(NO3)2
e 1,0 litri di una soluzione 0,20 M di NaCl, si avrà precipitazione di
PbCl2? (Ks=1,6·10-5 M)
Poiché il PbCl2 dissocia secondo l’equazione:
PbCl2(s) ⇄ Pb2+(aq) + 2 Cl-(aq)
i due ioni da considerare nelle due soluzioni sono Pb2+ e ClIl Pb(NO3)2 è solubile e dissocia completamente negli ioni Pb2+ e NO3per cui nella prima soluzione [Pb2+]=0,10 M.
Analogamente nella seconda soluzione [Cl-]=0,20 M.
Per prima cosa calcoliamo le concentrazioni di questi due ioni nella
soluzione risultante dopo il mescolamento.
I volumi delle due soluzioni mescolate sono V1=V2=1,0 litri e quindi dopo
il mescolamento il volume finale è:
Vfin= V1+V2= (1,0+1,0) L= 2,0 L
Nella soluzione iniziale di Pb(NO3)2 la concentrazione degli ioni Pb2+ è
0,10 M e quindi ci sono 0,10 mol di tale ione. Dopo il mescolamento, lo
stesso numero di moli è diluito nel volume finale di 2,0 litri e quindi la
sua concentrazione sarà:
[Pb2+]=0,1 mol/2,0 L=0,05 M
Analogamente la concentrazione degli ioni Cl- dopo il mescolamento sarà:
[Cl-]=0,2 mol/2,0 L=0,1 M
Si calcola QS per la reazione di equilibrio di solubilità:
QS=[Pb2+][Cl-]2=(0,05)·(0,10)2=5,0·10-4 M2
e lo si confronta con il valore dato KS=1,6×10-5 M2.
Poichè QS>KS, la reazione è spostata verso sinistra e quindi si ha la
precipitazione di PbCl2.
Man mano che PbCl2 precipita le concentrazioni di Pb2+ e Cldiminuiscono fino a che il loro prodotto ionico diventa uguale a KS e
la precipitazione si arresta.
Può essere interessante stabilire quanto dello ione Pb2+ inizialmente presente
rimane in soluzione dopo la precipitazione e quanto invece è precipitato come
PbCl2.
Siccome Pb2+ e Cl- sono stati mescolati in quantità stechiometriche
nessuno dei due è in eccesso e si ha [Pb2+]=½[Cl-]=x=ovvero S e quindi
all’equilibrio:
KS=[Pb2+]·[Cl-]2=(S)·(2S)2=4S3
-5
K
1,6
⋅
10
[Pb 2+ ] = S = 3 S = 3
= 1,6 ⋅10 -2 M
4
4
che corrisponde ad un numero di moli pari a:
[Pb2+]×
×Vfin= 1,6·10-2 M·2 L=0,032 mol
Le moli di Pb2+ inizialmente presenti erano 0,1 per cui ne sono precipitate:
0,068
× 100 = 68%
0,1-0,032=0,068 mol
cioè il
0,10
La massa effettiva di PbCl2 precipitata è
m PbCl2 = n PbCl2 ⋅ PM PbCl2 = 0,068 mol ⋅ 278,1 (g/mol ) = 18,9108 g
Da un punto di vista pratico a che serve conoscere i
prodotti di solubilità (KS), ad esempio: intonaci e pietre
Risale ad oltre due millenni fa la scoperta delle capacità “adesive”
delle malte:
La reazione si fa avvenire a T=800-900˚C (è una
reazione endotermica) e poiché è una reazione di
equilibrio bisogna allontanare la CO2 gassosa per
ottenere una conversione completa
CaCO3
calore (T=800-900°C)
CaO + CO2
La calce viva (ossido di calcio, CaO)
lentamente!
anche 9-12 mesi
+CO2
la calce spenta reagisce con la CO2 dell’aria e si
ritrasforma in carbonato di calcio
+H2O
reazione molto esotermica
Ca(OH2)
calce spenta
(idrossido di calcio Ca(OH)2)
che può succedere?
• malte, intonaci, pietre calcaree, sono quindi
costituite di (o contengono) carbonato di calcio:
SO2 da combustione + ossidazione (aria: O2+N2)
CaCO3
SO3 in acqua
CaSO4 + CO2
+H2O
CaSO4·2H2O
gesso
che può succedere?
Il calcare (CaCO3) e il gesso (CaSO4·2H2O; cioè solfato di
calcio più due molecole di acqua di idratazione) hanno
solubilità diversa (il gesso è circa 100 volte più solubile del
calcare):
CaCO3(s) ⇄
Ca2+
(aq)
+
CO32-(aq)
K S = [Ca 2+ ] ⋅ [CO 32− ] = 4,96 ⋅10 −9 [M 2 ] = S2
S = K S = 4,96 ⋅10 −9 = 7,04 ⋅10 −5 M
CaSO4(s) ⇄ Ca2+(aq) + SO42-(aq)
K S = [Ca 2+ ] ⋅ [SO 24− ] = 7,1 ⋅10 −5 [M 2 ] = S2
S = K S = 7,1⋅10 −5 = 8,43 ⋅10 −3 M
perciò:
il gesso viene portato via dall’acqua piovana molto più
facilmente
che può succedere?
statua
danneggiata
gesso formatosi in una
matrice di marmo
(solfatazione del marmo)
il solfato di calcio (gesso) è meccanicamente fragile; inoltre assorbe acqua
causando una espansione dei volumi con seri danni alla struttura di marmo
Esercitazione
Dal libro Nobile-Mastrorilli (Cap 15: Equilibri in soluzione:
pH e prodotto di solubilità), oltre a studiare gli esercizi
svolti, dovete essere in grado di svolgere i seguenti
problemi: Ks e solubilità (pag. 541-543)
1, 2, 3, 4, 5, 6, 7, 8.
Inoltre studiare le dispense tratte dal libro
Stechiometria per la chimica generale
di Paola Michelin Lausarot e Gian Angelo Vaglio
Cap 17 e svolgere i relativi esercizi.
Infine svolgere gli esercizi integrativi riportati
alla fine di questa lezione.
Si dissocia in Cu+ e SCN− (anione isotiocianato)
Periodato di torio (lV)
Svolgimento (punto d):
Ag 2SO 4 (s)
Eq)
2 Ag + (aq) + SO 24- (aq)
2S
K S = [Ag + ]2 ⋅ [SO 24− ] = 1,20 ⋅10 −5
S
–5
K
1,2
·
10
K s = [2S]2 ⋅ [S] ⇒ S = 3 S = 3
≅ 1,442 ⋅10 − 2 [mol ]
L
4
4
 mol 
S' mg  = S
⋅ PM Ag 2SO 4

 L 
 L 
mg
 g 
⋅
1000
 mol 
g


mg
 mol 
 g 
mg 
1000
4497
S' mg  = 1,442 ⋅10 − 2 
⋅
311,7936
⋅
≅
 mol 
 L 
 L 
g
 L 
Terminare l’esercizio da soli (punti a,b,c,e,f,g) prendendo le KS dalla Tab.15.3
Calcolare la solubilità espressa in mol/L del diioduro di piombo (PbI2):
(a) in acqua pura;
(b) in una soluzione 0,06 M di ioduro di potassio (sale solubile)
-9
3
Sapendo che K S = 8,49 ⋅ 10 (mol/L) . Svolgimento:
PbI 2 ( s )
(punto a):
i)
→
←
Pb 2+ ( aq ) + 2I − ( aq )
-S
Eq)
-2S
K s = 8,49 ⋅ 10 (mol/L) = S ⋅ (2S)
-9
(punto b):
i)
Eq)
PbI 2(s)
3
→
←
K S = 8,49 ⋅ 10 -9 (mol/L)3
2
-9
K
8,49
⋅
10
⇒ S=3 s =3
= 1,285 ⋅10 −3 (mol/L)
4
4
Pb 2+ (aq) + 2I − (aq)
-S
0,06
0,06 + 2S
2S <<< 0,06 ⇔ 0,06 + 2S ≈ 0,06
K s = [Pb 2+ ] ⋅ [I − ]2 = 8,49 ⋅ 10 −9
[S] ⋅ [0,06]2 = 8,49 ⋅ 10 −9
8,49 ⋅ 10 −9
−6
⇔ S=
=
2,36
⋅
10
(mol/L)
2
[0,06]
L’approssimazione 2S << 0,06 (mol/L) è verificata.
Calcolare la solubilità del PbCl2 (espressa in g/L) in una soluzione 0,10 M di
AlCl3 (sale solubile) sapendo che K S, PbCl 2 = 1,17 ⋅ 10 -5 (mol/L)3
Svolgimento:
PbCl 2 ( s )
i)
Eq)
→
←
Pb 2+ ( aq ) + 2 Cl - ( aq )
N.B. :
--
ma
S
0,3
0,3 + 2S
[AlCl3 ] = 0,1 M = [Al3+ ]
[Cl ] = 3 ⋅ [Al ] = 0,3 M
−
2S <<< 0,3 ⇔
3+
0,3 + 2S ≈ 0,3
K s = [Pb 2+ ] ⋅ [Cl − ]2 = 1,17 ⋅ 10 −5 =
[S] ⋅ [0,3]2 = 1,17 ⋅ 10 −5
1,17 ⋅ 10 −5
−4
⇔ S=
=
1,3
⋅
10
(mol/L)
2
[0,3]
L’approssimazione 2S << 0,3 (mol/L) è verificata.
mol
mol
g
g
g
S   = 5,41 ⋅10 −3
⋅ PM PbCl 2 = 1,3 ⋅10 − 4
⋅ 278,106
≅ 3,6154 ⋅10 − 2  
L
L
mol
L
L
Svolgimento:
a)
Pb(IO 3 ) 2 (s)
2+
Pb (aq)
+ 2 IO 3−
S
K s = [S] ⋅ [2S]2
(aq)
K s = [Pb 2+ ] ⋅ [IO3− ]2
2S
–13
K
3,68
·
10
⇒ S=3 s =3
= 4,51 ⋅10 −5 [mol ]
L
4
4
mg
 mol 
 g 
mg


S'
= S
⋅ PM Pb(IO3 ) 2 
⋅1000
⋅


 mL
g
 L 
 mol 
1
ml
1000
L
=
mg
1
 mol 
 g 
mg

= 4,51⋅10 
⋅
557,0054
⋅
1000
⋅
≅
0
,
0251

 mol 
 mL
g 1000 ml
 L 


L
−5
b)
HIO3 a pH=2
significa che [H3O+]=[H+]=10-pH
HIO3 è un acido forte:
[H + ] = [IO3- ] = 10 − pH = 10 −2 = 0,01 M
2+
Pb (aq)
+ 2IO 3- (aq)
Pb(IO 3 ) 2 (s)
K s = [Pb + + ] ⋅ [IO3- ]2
i)
-
0,01
eq)
s
0,01+2s
S << 0,01 ⇒ 0,01 + 2S ≈ 0,01
K s = [S] ⋅ [0,01]
2
Ks
3,68 · 10 –13
– 9 mol
⇒ S=
=
=
3,68
·
10
[
]
2
–4
L
1 · 10
[0,01]
mg
 mol 
S' mg  = S
⋅
PM
⋅
1000
⋅
Pb(IO3 ) 2

 ml
g
 L 
1
mL
1000
L
=
mg
1
 mol 
 g 
−6
= 3,68 ⋅10 −9 
⋅
557,0054
⋅
1000
⋅
≅
2
,
05
⋅
10
 mol 
g 1000 ml
 L 
L
L’approssimazione S << 0,01 (mol/L) è verificata
mg

 mL
Svolgimento:
a)
Ag 2 Cr2 O 7 (s)
+
2 Ag (aq)
+ Cr2 O 72- (aq) K s = [Ag + ]2 ⋅ [Cr2 O 72- ] = ?
2S
S
K s = [2S] ⋅ [S]
2
 mg 
S' 
100 mL 
 mol 

S
=
=

mg
1
 g 
 L  PM
1000
⋅
⋅
Ag 2 Cr2 O 7 
g 1000 ml
 mol 
L
 mg 
12,96 
12,96
100 ml 
 mol 

=
=
= 3,002 ⋅10 − 4 
mg
1
431,7238 ⋅100
L 
 g 

431,7238 
⋅1000
⋅

g 1000 ml
 mol 
L
K s = [2S]2 ⋅ [S]
−4 2
−4
K s = [2 ⋅ 3,002 ⋅10 ] ⋅ [3,002 ⋅10 ] = 1,082 ⋅10
b)
Ag 2 Cr2 O 7 (s)
2 Ag
+
(aq)
+ Cr2 O
i)
0,1
eq)
0,1+2S
−10
 mol 
 L 
3
27 (aq)
-S
S << 0,1 ⇒ 0,1 + 2S ≈ 0,1
Ks
1,082 ⋅10 −10
−8
K s = [0,1] ⋅ [S] ⇒ S =
=
=
1
,
082
⋅
10
[mol/L]
2
–2
[0,1]
1 · 10
2
 mol 
S' g  = S 
⋅ PM Ag 2Cr2O7

 L 
 L 
= 1,082 ⋅10
−8
 g 
 mol  =


L’approssimazione S << 0,1 mol/L
è verificata
 mol 
 g 
−6
4
31
,
7238
4
,
671
10
⋅
=
⋅
 L 
 mol 




g
L
 
Calcolare la solubilità, in moli/litro, di Cr(OH)3 in acqua pura e in una
soluzione tamponata a pH = 4,0, sapendo che KS dell’idrossido di
cromo(III) è uguale a 1,0·10−30 M4.
Svolgimento:
K s = [Cr + ] ⋅ [OH − ]3 = 1,0 ⋅10 −30 M 4
In acqua pura
Cr(OH) 3(s)
←
→
3+
(aq)
Cr
+ 3 OH
S
3S
K s = [S] ⋅ [3S]3 = 27S4
−
(aq)
−30
4
⋅
K
1,0
10
M
s
=4
≅ 1,387 ⋅10 −8 M
S=4
27
27
In una soluzione tamponata a pH = 4,0
pH = 4 ⇒ pOH = 10 ⇒ [OH − ] = 1,0 ⋅10 − pOH = 1,0 ⋅10 −10 M
i)
eq)
Cr(OH) 3(s)
←
→
3+
−
Cr(aq)
+ 3 OH (aq)
-1,0·10−10
S
1,0·10−10
[S] ⋅ [1,0 ⋅10 −10 ]3 = 1,0 ⋅10 −30 M 4
La soluzione tampone fa
sì che rimanga costante
S = 1,0 M
Svolgimento (punto d):
Il problema esplicitamente ci dice che avremo un precipitato, tuttavia dimostriamolo
[ZnCl2 ] = 1,466  mol 
400 mL di cloruro di zinco 1,466 M
[Zn ]
2+
ZnCl2 (aq) → Zn 2+ (aq) + 2Cl − (aq)
 L 
 mol 
= 1,466 

 L 

[Cl ] = 2 ⋅1,466  mol
L 
−

 mol 
[KF] = 0,75  
 L 
600 mL di fluoruro di potassio 0,75 M

[K ] = 0,75  mol
L 
+
KF(aq) → K
+
(aq)
+F
−

(aq)



[F ] = 0,75  mol
L 
−


Formalmente è come se avvenisse la reazione:
ZnCl2 + 2 KF → ZnF2 + 2 KCl
Ma l’unico sale insolubile è il fluoruro di zinco (vedi tabella 15.3)
La reazione vera è quella in forma ionica :
Zn
2+
(aq)
+2F
−
(aq)
→ ZnF2 ( s )
Che è l’inverso dell’equilibrio di solubilità:
ZnF2 ( s )
→
←
Zn 2+ (aq) + 2 F− (aq)
Si ha precipitato se
K S = [ Zn 2+ ] ⋅ [F− ]2 = 3,04 · 10 –2 M 3
QS = [ Zn 2+ ]0 ⋅ [F− ]02 > K S = 3,04 · 10 –2 M 3
N.B.: Concentrazioni dopo la diluizione
Dobbiamo calcolarle con la formula delle diluizioni (Mi·Vi= Mf·Vf):
[Zn 2+ ]0 =
n Zn 2+
Vfinale,soluzione
=
VZnCl2 ⋅ [ ZnCl 2 ]
VZnCl2 + VKF
=
0,40 (L) ⋅1,466 (mol/L) 0,5864 mol
=
= 0,5864 (mol/L)
0,40 (L) + 0,60 (L)
1,00 L
[F− ]0 =
n F−
Vfinale,soluzione
=
VKF ⋅ [KF]
0,600 (L) ⋅ 0,75 (mol/L) 0,45 mol/L
=
=
= 0,45 (mol/L)
VKF + VZnCl2
0,60 (L) + 0,40 (L)
1,00 L
QS = [Zn 2+ ]0 ⋅ [F− ]02 = 0,5864 (mol/L) ⋅ [0,45 (mol/L)]2 = 1,18746 · 10 –1 M 3 > K S = 3,04 · 10 –2 M 3
Si ha formazione di precipitato …… ma quanto ne precipita?
Possiamo ragionare in moli o con le concentrazioni dopo la diluizione (visto che il
volume è lo stesso adesso: 1 litro)
Moli
I)
∆)
Tot)
Conc
I)
Eq)
Zn 2+ (aq) + 2 F− (aq) → ZnF2 ( s )
0,45
− 0,45
−
+ 0,225
0,3614
0
0,225
[Zn 2+ ] =
0,3614 mol
= 0,3614 M
L
0,5864
− 0,225
ZnF2 ( s )
→
←
Zn 2+ (aq) + 2 F − (aq)
0,3614
−
0,3614 + S
2S
Moli precipitate a cui
tuttavia dobbiamo
sottrarre quelle che si
risolubilizzano per
l’equilibrio
K S = [ Zn 2+ ] ⋅ [F− ]2 = 3,04 · 10 –2 M 3 = (0,3614 + S) ⋅ ( 2S)
2
Pongo in prima approssimazione:
Purtroppo S è
confrontabile con
0,3614
0,3614 + S ≅ 0,3614
3,04 · 10 –2
mol
S=
= 0,145
0,3614 ⋅ 4
L
3,04 · 10 –2 = (0,3614) ⋅ ( 2S)
2
Piuttosto che risolvere l’equazione di
3° grado in S scelgo di usare un
metodo iterativo
–2
3,04 · 10 = (0,3614 + 0,145) ⋅ ( 2S')
3,04 · 10 –2
mol
S' =
= 0,1225
(0,3614 + 0,145)⋅ 4
L
3,04 · 10 –2 = (0,3614 + 0,1225) ⋅ ( 2S' ')
3,04 · 10 –2
mol
S' ' =
= 0,1253
(0,3614 + 0,1225) ⋅ 4
L
2
2
3,04 · 10 = (0,3614 + 0,1253) ⋅ ( 2S' ' ')
–2
2
3,04 · 10 –2
mol
S' ' ' =
= 0,125
(0,3614 + 0,1253) ⋅ 4
L
n ZnF2 ridisciolt e = S' ' '⋅Vsoluzione = 0,125 (mol/L ) ⋅1[L] = 0,125 mol
converge
n ZnF2 precipitat e effettive = 0,225 mol − 0,125 mol = 0,100 mol
m ZnF2 precipitat o = 0,100 mol ⋅ PM ZnF2 = 0,100 mol ⋅103,39
g
= 10,339 g
mol
Terminare l’esercizio da soli (punti a,b,c) prendendo KS dalla Tab.15.3
Esercizi riassuntivi e integrativi
I) Il carbonato di calcio, CaC03, utilizzato dai sistemi viventi per costruire le conchiglie, si
deposita in strati calcarei che, dopo compressione e riscaldamento, portano alla formazione
del marmo. Determinare la solubilità in mg/L del carbonato di calcio sapendo che il suo KS è
pari a 8,7·10-9 M2. [R. 9,34 mg/L]
II) Calcolare la solubilità dell'idrossido rameico (in g/L) in soluzione acquosa tamponata a
pH 7,0. Il prodotto di solubilità dell'idrossido rameico è di 2,2·10-20. [2,1·10-4 g/L]
III) Calcolare la solubilità (in g/L) dell’idrossido ferroso Fe(OH)2 in una soluzione 0,1 M
di NaOH con KS=1,52·10−14 M3. [1,36·10-10 g/L ]
IV) Il solfato rameico è un efficace alghicida, e talora viene aggiunto all’acqua delle
piscine per evitare la crescita delle alghe. Quale deve essere il pH massimo dell’acqua di
una piscina per evitare la precipitazione dell'idrossido rameico (KS,Cu(OH)2 = 1,6·10-19
M3) quando si aggiungono 4,0 g di solfato rameico pentaidrato (CuSO4·5 H2O) ogni 10
litri d'acqua? [pH=6,0]
V) Il fosfato tricalcico (KS, Ca3(PO4)2= 1,3·10-32 M5) è uno dei componenti più comuni dei
calcoli renali (altri sali comuni in queste affezioni sono: carbonato di calcio, ossalato di
calcio, fosfato ammonico magnesiaco). Qual è la concentrazione, in grammi/litro, di
fosfato tricalcico nelle urine di un paziente che abbia calcoli renali di questo tipo?
[5,1·10-5 g/L]
Esercizi riassuntivi e integrativi
VI) Molte acque naturali contengono sali di ferro provenienti dai vari minerali ferrosi
attraverso cui le acque sono filtrate. Nella maggioranza dei casi le acque naturali sono
leggermente alcaline. L'idrossido ferrico (di colore giallastro) è talmente poco solubile
che lo ione ferrico è presente nelle acque naturali come idrossido ferrico solido
finemente disperso (stato colloidale). In zone dove il contenuto di ferro nell'acqua è
moderatamente elevato, non è raro trovare acque di colore giallognolo a causa della
torbidità dovuta all'idrossido ferrico. Quale valore massimo di pH dovrebbe avere
un’acqua naturale che contenga 33 mg/L di ione ferrico affinché non si formi precipitato
di idrossido ferrico? Il prodotto di solubilità dell'idrossido ferrico è di 6·10-38 M4. [2,67]
VII) L'applicazione dei raggi X in medicina è estremamente diffusa. L'osservazione
delle cavità interne del corpo richiede il riempimento di tali cavità con materiali di
contrasto più opachi o più trasparenti ai raggi X rispetto ai tessuti circostanti. Il
solfato di bario (BaSO4), che è un sale insolubile opaco ai raggi X (KS = 1,1·10-10 M2),
viene impiegato negli esami del tratto gastrointestinale. Lo ione bario però è tossico,
per cui è necessario, onde diminuirne la solubilità per effetto dello ione comune,
aggiungere alla sospensione di solfato di bario un eccesso di ioni solfato. Nella
preparazione di una sospensione acquosa di solfato di bario viene aggiunta una quantità
di epsomite (solfato di magnesio eptaidrato: MgSO4·7H2O, molto solubile), tale da
fornire una concentrazione 0,015 M in ioni magnesio. Qual è la concentrazione molare
di ioni bario liberi in questa sospensione? Quale sarebbe stata se non si fosse aggiunta
epsomite? [7,3·10-9 M; 1,0·10-5 g/L]
Esercizi riassuntivi e integrativi
1) Una soluzione satura di cloruro di piombo(II) contiene, a 20°C, 4,5 g di sale per litro. Si
calcoli il valore del prodotto di solubilità del cloruro di piombo a 20°C. [KS=1,69·1O−5 M3]
2) A 25°C, il prodotto di solubilità del cromato di argento (Ag2CrO4) vale KS=1,9·1O−12 M3. Si
calcoli la massa in grammi di cromato di argento che si scioglie in 2,8 L di a) acqua, b) una
soluzione 0,250 M di nitrato di argento (AgNO3) e c) una soluzione 0,250 M di cromato di
sodio (Na2CrO4).
[a) 7,25·1O-2 g, b) 2,824·1O-8 g, c) 1,281·1O-3 g]
3) Si calcolino le concentrazioni degli ioni stronzio e solfato presenti nella soluzione
ottenuta mescolando 2,0 L di una soluzione 0,10 M di cloruro di stronzio con 0,50 L di una
soluzione 0,40 M di solfato di sodio. Alla temperatura dell'esperienza, il prodotto di
solubilità del solfato di stronzio vale KS=7,6·1O−7M2. ([Sr2+]= [SO42-] =8,72·10-4 M)
4) Una soluzione viene preparata sciogliendo 1,00 g di nitrato di argento (AgNO3) e 1,50 g di
cromato di potassio (K2CrO4) in tanta acqua da avere un volume finale di soluzione pari a 25,0
mL. Sapendo che, alla temperatura dell'esperienza, il prodotto di solubilità del cromato di
argento vale KS=1,9·1O-12 M3, si calcoli la concentrazione di tutte le specie ioniche presenti
nella soluzione.
([NO3-]=0,235 M, [K+]=0,618 M, [CrO42-]= 0,191 M, [Ag+]=3,16·1O-6 M]
5) Ad una certa temperatura, il prodotto di solubilità del cloruro di piombo(II) vale
KS=1,70·10-5 M3. Si calcoli la solubilità del sale a) in acqua pura e b) in una soluzione 3,0 M di
acido cloridrico, esprimendola in g/L. [a) 4,51 g/L; b) 5,25·10−4 g/L]
6) La solubilità del carbonato di calcio in acqua vale S=7,04 mg/L, a 25°C. Si calcoli la perdita
in peso di un precipitato di carbonato di calcio se questa viene lavato a) con 1,0 L di acqua; b)
con 1,0 L di una soluzione 0,02 M di carbonato di sodio.
[a) 7,04 mg, b) 2,48·10−2 mg]
Esercizi riassuntivi e integrativi
7) Il prodotto di solubilità del bromato di argento vale, a 25°C, Ks = 5,8 . 1O−5M2. Si calcoli la
concentrazione degli ioni presenti in una soluzione ottenuta mescolando 40,0 mL di una
soluzione 0,02 M di nitrato di argento (AgNO3) con 60,0 mL di una soluzione 0,04 M di
bromato di potassio (KBrO3).
([K+]=2,4·1O-2 M; [NO3-]=8,0·10-3M; [Ag+]=3,03 ·10-3M; [BrO3-]=1,87·10-3M]
8) Quando 50,O mL di una soluzione 4,0·10-2M di LaCl3 sono mescolati con 50,0 mL di una
soluzione 9,6 ·10-2 M di NaIO3 si ottiene un precipitato di La(IO3)3 del peso di 663,6 mg. Si
calcoli il valore del prodotto di solubilità dello iodato di lantanio e la solubilità della sua
soluzione satura.
[Ks = 5,8·10-8 M4; sol. sat.: S= 6,81·10-3 M]
9) 500,0 mL di una soluzione 0,10 M di nitrato di argento vengono mescolati con 1500,0 mL di
una soluzione 0,10 M di cromato di potassio. Si ha la precipitazione di cromato di argento, il
cui prodotto di solubilità , alla temperatura dell'esperienza, vale Ks = 1,0·10-12M3. Si calcoli la
concentrazione dello ione argento rimasto nella soluzione. ([Ag+]=4·10-6 M)
10) Si mescolano 150 ml di una soluzione 0,4 M di MnCl2 con 230 ml di una soluzione 0,2 M di
K2S. Calcolare i grammi di MnS che precipitano e le concentrazioni degli ioni Mn2+ e S2− dopo il
mescolamento. Per MnS, KS = 3,2·10−11 M2.
[mMnS : 4,002 g; [ Mn2+]=0,037 M; [S2−]= 8,64 ·10−10 M]
11) Calcolare quanti grammi di Ca3(PO4)2 che ha KS=1,4 ·10−30 M5 si sciolgono in 100 mL di
una soluzione 0,1 M di CaCl2. [5,8·10−13g]
12) Si mescolano 120 mL di una soluzione 0,15 M di Pb(NO3)2 con 250 mL di una soluzione
0.,03M di K2CrO4. Sapendo che per PbCrO4 KS=1,77·10−14 M2, trovare i grammi di cromato di
piombo che precipitano e le concentrazioni residue di Pb2+ e di CrO42− dopo la precipitazione.
[mPbCrO4 =2,42 g;[ Pb2+] = 2,842 M; [CrO42−]=6,23·10−13 M]
Chimica
(a.a. 2011/2012, 6CFU)
Elettrochimica:
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
trasformazione di energia chimica in elettrica e viceversa (Elettrochimica)
brevi cenni sulla conducibilità degli elettroliti (conduttori di II specie)
il potere ossidante
la pila Daniell ed il ponte salino
schematizzazione di una pila
misura del potenziale di elettrodo e forza elettromotrice
potenziale standard di riduzione E°
la serie elettrochimica
l’equazione di Nernst
le pile da un punto di vista termodinamico
la f.e.m. e la dimostrazione della legge di Nernst
tipi di elettrodi :1a specie e 2a specie
le pile di concentrazione
Esercitazione sulle pile.
Esercizi riassuntivi e integrativi
ELETTROCHIMICA
TRASFORMAZIONE DELL’ENERGIA
CHIMICA
(PROVENIENTE
DA
REAZIONI SPONTANEE) IN ENERGIA
ELETTRICA (“ ELETTRICITÀ”).
TRASFORMAZIONE DELL’ENERGIA
ELETTRICA IN ENERGIA CHIMICA
(REAZIONI NON SPONTANEE)
PILE
ELETTROLISI
(CELLE GALVANICHE o VOLTAICHE )
(CELLE ELETTROLITICHE)
Brevi cenni sulla conducibilità degli elettroliti
Classificazione di
conduttore
Conduttori di I specie
(metallici)
Meccanismo di
conduzione
Spostamento di elettroni
All’aumentare della
temperatura la conducibilità
diminuisce
Conduttori di II
specie
(elettrolitici)
Spostamento di ioni
positivi e negativi
All’aumentare della
temperatura la conducibilità
aumenta
I sistemi
elettrochimici
Sono costituiti da (almeno) due elettrodi (conduttori di 1a
specie) e da un’elettrolita (conduttore 2a specie).
Quando il sistema elettrochimico è percorso da corrente
elettrica, questa è corrente elettronica negli elettrodi
e nel circuito esterno, ed è corrente ionica
nell’elettrolita.
• Nel primo caso i portatori di carica elettrica sono gli
elettroni, nel secondo sono ioni.
• Contemporaneamente, agli elettrodi avvengono reazioni
elettrochimiche (redox = ossidoriduzioni).
Due esperimenti:
(1)
Nessuna reazione
Cu
Cu(ss) + Zn2+(aq)
Cu(
aq) → Cu2+(aq)
aq) + Zn(
Zn(s)
Zn2+
(2)
Cu2+
Zn
D’altro canto, avviene
la seguente reazione :
Cu2+(aq
aq)) + Zn
Zn((s) → Cu(
Cu(ss) + Zn2+(aq
aq))
potere ossidante di Cu2+/Cu > potere ossidante di Zn2+/Zn
Cu
Zn
H2
H+
H+
2 H+(aq
aq)) + Cu(s
Cu(s) → H2(g) + Cu2+(aq
aq))
2 H+(aq
aq)) + Zn(s
Zn(s) → H2(g) + Zn2+(aq
aq))
pot. oss. Cu2+/Cu > pot. oss. H+/H2 > pot. oss. Zn2+/Zn
Cu
Ag+
Zn
Ag+
2 Ag+(aq
aq)) + Cu(s
Cu(s) → 2 Ag(s
Ag(s) + Cu2+(aq
aq))
Ag+/Ag
Cu2+/Cu
H+/H2
Zn2+/Zn
Scala qualitativa del potere ossidante
Cu2+(aq) + Zn(s) → Cu(s) + Zn2+(aq)
Zn(s) → Zn2+(aq) + 2 e-
ossidazione (zona anodica)
Cu2+(aq) + 2 e- → Cu(s)
riduzione (zona catodica)
Zn
e-
Zn2+
Cu
Cu2+
Se provo a collegare le due barrette metalliche si verifica un
flusso di elettroni e quindi una corrente elettrica (PILA). Tale
corrente, tuttavia, cesserà immediatamente di esistere.
Perché ?
Innanzitutto, dobbiamo tener conto che
(1) la
che è
(2) la
che è
soluzione di ioni Zn2+ è una soluzione di ZnSO4, elettrolita forte (α
α=1)
totalmente dissociata in Zn2+ e SO42soluzione di ioni Cu2+ è una soluzione di CuSO4, elettrolita forte (α
α=1)
totalmente dissociata in Cu2+ e SO42-
Quando gli elettroni passando dall’elettrodo di Zn a quello di Cu,
neutralizzano gli ioni Cu2+ della soluzione che istantaneamente si depositano
come atomi neutri sull’elettrodo stesso. D’altra parte all’elettrodo di Zn, al
quale sono stati sottratti elettroni, manda in soluzione altri ioni Zn2+ per
reintegrare gli elettroni perduti, ma anche questi nuovi elettroni passano
nell’elettrodo di Cu ove neutralizzano altri ioni Cu2+ , che si depositano; e
così via ………..
Il descritto meccanismo va però completato: infatti quanto detto
comporta che, appena chiuso il circuito esterno, la soluzione anodica sia
carica positivamente (formazione di ioni Zn2+ ) e quella catodica sia carica
negativamente (scomparsa di ioni Cu2+): ciò deve arrestare il
funzionamento della pila, perché risultano impedite, per azione
elettrostatica, sia l’ulteriore formazione di ioni Zn2+ che l’ulteriore
scarica di ioni Cu2+.
Zn
+ +
+ ++
Eccesso di cariche
positive dovute a ioni Zn2+
Cu
-- -Eccesso di cariche
negative dovute a ioni SO42-
In qualche modo, perché continui a fluire corrente (a funzionare la pila),
dobbiamo far in modo che gli ioni di Zn2+ migrino a destra e gli ioni SO42- a
sinistra. Ciò significa che dobbiamo mettere in contatto le due soluzioni: ma
così non avremmo più una pila perché si verificherebbe la reazione di
ossidoriduzione !!!!!
Questo fenomeno è aggirato tramite l’utilizzo di un setto poroso (membrana)
oppure un ponte salino. Quest’ultimo è costituito da una soluzione concentrata di
un sale, avente lo scopo di mantenere l’elettroneutralità delle due soluzioni
durante il funzionamento della cella galvanica.
Riassumendo: in assenza di un ponte salino una cella
galvanica (detta indifferentemente: cella voltaica o pila
voltaica o cella galvanica o semplicemente pila) non può
funzionare perché genererebbe due soluzioni non
elettroneutre:
difetto
di ioni SO42Zn(s) + Cu2+(aq)
eccesso
di ioni SO42Zn2+(aq) + Cu(s)
Una importante convenzione da ricordare
L’elettrodo dove avviene la riduzione si dice catodo ed in una
pila è il polo positivo (+)
L’elettrodo dove avviene la ossidazione si dice anodo ed in una
pila è il polo negativo (-)
Voltmetro
Zn
-
+
Cu
∆E = 0
Cu2+
Zn2+
Cl- ← ponte salino → K+
Il sistema (elettrochimico) costituito da due elettrodi immersi i due
opportune soluzioni separate fra loro da un setto poroso (o un ponte
salino), prende il nome di pila elettrica (o cella galvanica o cella voltaica)
ed ha una straordinaria importanza teorica e pratica.
UNA CELLA GALVANICA: la pila Daniell
Zn
voltmetro
semicella
semicella
Zn2+/Zn
Cu2+/Cu
2e- + Cu2+
Zn2+ + 2e-
catodo
anodo
Zn + Cu2+
Zn2+ + Cu
Cu
La pila Daniell:
ponte salino
Reazione all’anodo =
ossidazione:
Reazione al catodo =
riduzione:
Zn(s) → Zn2+(aq) + 2e-
Cu2+(aq) + 2e- → Cu(s)
La pila Daniell:
Setto poroso (membrana)
Riepilogando:le due versioni della Pila Daniell
e-
e-
V
V
(-)
Zn
Zn2+(aq) + SO42-(aq)
(+)
Setto
poroso
(-)
Cu
Zn
Cu2+(aq) + SO42-(aq)
Cu2+(aq) + 2 e- → Cu(s) Riduzione
Zn(s) → Zn2+(aq) + 2 eZn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s)
Zn2+(aq) + SO42-(aq)
Catodo (polo +)
Ossidazione
Ponte
salino
(+)
Cu
Cu2+(aq) + SO42-(aq)
Zn
Anodo (polo -)
Reazione totale della pila
Cu2+(aq)
Schematizzazione di una pila:
Indicare SEMPRE la polarità (+; -)
Metallo
M()
Composti
allo stato
solido e/o
gassoso
(indicare P)
M()
Composti
in
soluzione
(Cmolare)
ponte salino o membrana
Ad esempio, la Pila già incontrata (Daniell):
Zn(−)
Cu(+)
++
Zn + + (C Zn ++ ) Cu + + (CCu )
oppure
( −)
Zn
Composti
allo stato
solido e/o
gassoso
(indicare P)
Composti
in
soluzione
(Cmolare)
Zn(−)
oppure
(+)
[Zn + + ] = x M [Cu ++ ] = x M Cu
Cu(+ )
[Zn + + ] = x M [Cu + + ] = x M
oppure:
(−) Zn
[Zn + + ] = x M [Cu + + ] = x M Cu (+)
Misura del potenziale di elettrodo e Forza elettromotrice
Per misurare il potenziale di un elettrodo bisognerebbe disporre di uno strumento da
inserire all’interfaccia tra la fase solida (metallo) e quella liquida (soluzione): ciò è,
ovviamente, impossibile. Poiché il valore assoluto del potenziale dell’elettrodo (e della
relativa coppia redox) non può essere conosciuto, bisogna assegnargliene uno relativo,
riferito a una coppia alla quale viene attribuito arbitrariamente il valore zero: a tale
scopo si deve costruire una pila con l’elettrodo in esame e con quello della coppia di
riferimento e misurarne la differenza di potenziale, con uno strumento, il
potenziometro, che consente di ottenerne il valore senza che la pila eroghi corrente.
Questa differenza di potenziale è la massima che si possa ottenere tra i due
elettrodi e prende il nome di forza elettromotrice (f.e.m.): se durante la misura la
pila erogasse corrente, come avviene quando si usa un comune voltmetro, si avrebbe
una caduta di tensione e il valore misurato sarebbe inferiore alla fem. Indicando con
∆E la forza elettromotrice e con EC ed EA i potenziali del catodo (+) e dell’anodo (–),
si può scrivere
∆E = EC – EA
o, con la notazione che indica il segno dell’elettrodo:
∆E = E(+) – E(–)
Più tardi, torneremo sul significato termodinamico di forza elettromotrice.
Necessità di poter confrontare quantitativamente il potere
ossidante o riducente di una qualsivoglia coppia redox!
Elettrodo standard a idrogeno
Elettrodo di riferimento: è
stato deciso di misurare la
tendenza riducente o ossidante
di ciascuna coppia redox nei
confronti di questo elettrodo
standard.
Potenziale standard di riduzione E°:
Ox + ne
-
→ Red
Potenziale relativo alla semireazione di riduzione.
Si costruisce una scala di potenziali di riduzione
rispetto al potenziale dell’elettrodo standard a
idrogeno.
Condizioni standard: la temperatura è di 25°C
(298,15 K); tutte le specie in soluzione hanno
concentrazione 1 M; tutte le specie gassose hanno
pressione di 1 atm; tutti i solidi ed i liquidi puri
hanno attività unitaria.
Elettrodo standard di riferimento:
H+(aq) + e- → ½ H2(g)
E°H /H = 0 V
+
H2(1 atm)
2
Pt
25
25°°C = 298 K
[H+]= 1 M; pH=0
Potenziale standard di riduzione:
riduzione:
Cu2+(aq) + 2 e- → Cu(s)
E°= + 0,342 V
H2(1 atm)
Cu
Pt
25
25°°C
[Cu2+]=1,0 M
pH=0
H2(g) + Cu2+(aq) → 2 H+(aq) + Cu(s)
∆E = E C - E A = E°Cu 2+ /Cu − E°H + /H = 0,342V ⇒ E°Cu 2+ /Cu = ∆E + E°H + /H = 0,342V + 0V ⇒ E°Cu 2+ /Cu = +0,342V
2
2
Potenziale standard di riduzione:
Zn2+(aq) + 2 e- → Zn(s)
H2(1 atm)
pH=0
E°= - 0,762 V
Zn
Pt
25°
25°C
[Zn2+]=1,0 M
2 H+(aq) + Zn(s) → H2(g) + Zn2+(aq)
∆E = E C - E A = E° H + /H − E° Zn 2+ /Zn = 0,762V ⇒ E° Zn 2+ /Zn = E° H + /H − ∆E = 0V - 0,762V ⇒ E° Zn 2+ /Zn = −0,762V
2
2
Potenziale standard di riduzione:
NO3-(aq) + 3 e- + 4 H+(aq) → NO(g) + 2 H2O(l)
H2 (1 atm)
Pt
Pt
25°°C
25
pH=0
E°°= + 0,957 V
NO (1 atm)
[NO3-] = 1,0 M
pH = 0
2NO3-(aq) + 3H2 + 2 H+(aq) → 2NO(g) + 4 H2O(l)
∆E = E C - E A = E° NO - /NO − E°H + /H = 0,957V ⇒ E° NO - /NO = ∆E + E°H + /H = 0,957V + 0V ⇒ E° NO - /NO = +0,957V
3
2
3
2
3
La serie elettrochimica dei potenziali standard di riduzione (25°C)
Semireazione
E° (V)
Semireazione
E° (V)
F2(g) + 2e- ⇔ 2F-
+2,866
2H+(aq) + 2e- ⇔ H2(g)
+0,000
PbO2(s) + SO42-(aq) + 4H+ + 2e- ⇔ PbSO4(s) + H2O +1,691
Sn2+(aq) + 2e- ⇔ Sn(s)
-0,130
HClO2(aq) + 3H+(aq) + 3e- ⇔ Cl-(aq) + 2H20
+1,560
Ni2+(aq) + 2e- ⇔ Ni(s)
-0,257
+1,507
Co2+(aq) + 2e- ⇔ Co(s)
-0,280
+1,455
PbSO4(s) + 2e- ⇔ Pb(s) + SO42-(aq)
-0,360
+1,498
Cd2+(aq) + 2e- ⇔ Cd(s)
-0,403
Fe2+(aq) + 2e- ⇔ Fe(s)
-0,447
Cr3+(aq) + 3e- ⇔ Cr(s)
-0,744
Zn2+(aq) + 2e- ⇔ Zn(s)
-0,762
-
MnO4 (aq) +
8H+
5e-
(aq)
+
+
2e-
PbO2(s) +
4H+
(aq)
Au3+
3e-
⇔ Au(s)
(aq)
-
+
BrO3 (aq) +
Cl2 (g) +
O2(g) +
6H+
2e-
4H+
⇔
(aq) +
Cl-
(aq) +
⇔
⇔
5e-
Mn2+
Pb2+
(aq)
(aq)
+ 4H20
+ 2H2O
⇔ Br2(l) + 3H2O
(aq)
4e-
⇔ 2H2O
+1,482
+1,358
+1,229
Br2 (aq) + 2e- ⇔ 2Br-(aq)
+1,066
NO3-(aq) + 4H+(aq) + 3e- ⇔ NO(g) + 2H2O
+0,962
2H2O(aq) + 2e- ⇔ H2(g) + 2OH-(aq)
-0,828
Ag+(aq) + e- ⇔ Ag(s)
+0,800
Mg2+(aq) + 2e- ⇔ Mg(s)
-2,372
Fe3+(aq) + e- ⇔ Fe2+(aq)
+0,771
Na+(aq) + e- ⇔ Na(s)
-2,710
I2(s) + 2e- ⇔ 2I-(aq)
+0,536
Ca2+(aq) + 2e- ⇔ Ca(s)
-2,868
Cu+(aq) + e- ⇔ Cu(s)
+0,521
K+(aq) + e- ⇔ K(s)
-2,931
Cu2+(aq) + 2e- ⇔ Cu(s)
+0,342
Li+(aq) + e- ⇔ Li(s)
-3,040
Sul Nobile-Mastrorilli la trovate alla tabella 16.1 di pag. 558
0,268
Per la pila Daniell abbiamo,ad esempio, in condizioni standard:
∆E = E − E = 0,342 − (−0,762) = 1,104 V
o
+
o
−
-
+
Zn
[Zn2+]=1,0 M
Ossidazione
(anodo)
Cu
25
25°°C
[Cu2+]=1,0 M
Riduzione
(catodo)
Curiosità: la pila Daniell fu la prima cella galvanica ad essere prodotta su scala
industriale per essere utilizzata come generatore di energia elettrica necessaria
al funzionamento delle prime linee telegrafiche e telefoniche.
Per calcolare il potenziale di un elettrodo non allo stato standard (allo
stato attuale) si usa l’equazione di Nernst (legge di Nernst):
ν0xOx + ne– → νRedRed
Potenziale
attuale
Concentrazione
molare della specie
ossidata
Potenziale
standard
RT [Ox ]
E = E° +
ln
ν Red
nF [Red ]
ν Ox
Walter Hermann Nernst
Briesen 1864 – Berlino 1940
Premio Nobel per la Chimica 1920
A 25°C:
Numero degli
elettroni scambiati
nella semireazione
Costante di
Faraday
[
0,0591
Ox]
E = E° +
log 10
ν Red
n
[Red ]
ν Ox
Concentrazione
molare
della specie ridotta
νOx coefficiente stechiometrico di Ox; νRed coefficiente stechiometrico di Red
Vediamo le pile da un punto di vista termodinamico (interpretazione
termodinamica delle pile)
Zn
H2
[H+] =1 M
Zn ( s ) + 2 H + ( aq ) → Zn + + ( aq ) + H 2 ( g ) + Q
Zn( s ) → Zn + + (aq ) + 2e −
2 H + (aq ) + 2e − → H 2 ( g )
Se R → ∞ Q ≠ Q1
Zn ( s ) + 2 H + ( aq ) → Zn + + ( aq ) + H 2 ( g ) + Q1
Perché? Che significa da un punto di vista termodinamico?
Per la reazione di ossidoriduzione
Zn ( s ) + 2 H + ( aq ) → Zn + + ( aq ) + H 2 ( g ) + Q
∆U = Q − L
vale
Nella Pila
dove
L
é solo lavoro di tipo PV :
L = P∆V
Zn ( s ) + 2 H + ( aq ) → Zn + + ( aq ) + H 2 ( g ) + Q1
∆U = Q1 − L − Lutile dove Lutile = Lelettrico
Se R→∞ significa che I≈0, vale a dire circuito aperto: condizioni di
reversibilità, Q1 diventa un differenziale esatto
dQ1 = TdS
⇔
Q1 = T ∆ S
∆ U = T ∆ S − P ∆ V − Lelettrico
− Lelettrico = ∆ U + P ∆ V − T ∆ S
− Lelettrico = ∆ H − T ∆ S
− Lelettrico = ∆ G = − Lutile
Lelettrico = carica × differenza di potenziale = q ⋅ V
[Coulomb × Volt
= Joule ]
La costante di Faraday F è la carica
di una
mole di elettroni,
F=96485 C/mol di e-;
(F/NA)=(96485 C/mol/6,022·10+23 elettrone/mol)=1,602177·10-19C:
carica di un elettrone.
L’energia chimica massima della pila che può essere
convertita in energia (lavoro) elettrica è la variazione di
energia libera di Gibbs (∆
∆G):
∆G = – n·F·∆
∆E
dove n·F = q è la carica e ∆E è la differenza di potenziale
(V) a circuito aperto che è la cosiddetta
forza
elettromotrice (acronimo: f.e.m) e rappresenta la massima
d.d.p. ottenibile da una pila.
f.e.m.
(acronimo di forza elettromotrice)
Si definisce forza elettromotrice (f.e.m.) di
una pila la differenza di potenziale (d.d.p.)
MASSIMA che può esistere tra i due
elettrodi di una pila (a resistenza infinita,
cioè a circuito aperto: corrente zero).
Essa misura la tendenza della reazione ad
avvenire (SPONTANEITÀ).
Si può misurare con un opportuno strumento
che si chiama POTENZIOMETRO.
Dimostrazione della legge di Nernst:
Si considerino le due coppie redox Ox1/Red1 e Ox2/Red2; se il potenziale E1
della coppia 1 è maggiore di quello E2 della coppia 2, la reazione spontanea
tra la forma ossidata Ox1 della coppia ossidante e quella ridotta Red2 della
coppia riducente è
Ox1 + Red2 → Red1 + Ox2
Se n1 e n2 sono gli elettroni in gioco nelle due semireazioni, queste possono
essere scritte nella forma:
Ox1 + n1 e– → Red1
Red2 → Ox2 + n2 e–
e, indicando con n il minimo comune multiplo tra n1 e n2 e con a e b due numeri
primi tra loro tali che:
a n1 = b n2 = n
la reazione bilanciata è
a Ox1 + b Red2 → a Red1 + b Ox2
Dimostrazione della legge di Nernst:
a Ox1 + b Red 2 → a Red1 + b Ox2
∆G = ∆G ° + RT ln Q < 0
∆G = −nF∆E
Red 1 ] ⋅ [Ox 2 ]
[
Q=
[Ox1 ]a ⋅ [Red 2 ]b
a
b
∆G° = −nF∆E °
RT [Red 1 ] ⋅ [Ox 2 ]
∆E = ∆E ° −
ln
a
b
nF [Ox1 ] ⋅ [Red 2 ]
a
b
[
2,3 ⋅ RT
Red1 ] ⋅ [Ox 2 ]
∆E = ∆E° −
log 10
a
b
nF
[Ox1 ] ⋅ [Red 2 ]
a
b
[
0,0591
Red 1 ] ⋅ [Ox 2 ]
∆E = ∆E° −
log
n
[Ox1 ]a ⋅ [Red 2 ]b
a
b
0,0591
[
Red 1 ] 0,0591
[
Ox 2 ]
E1 − E 2 = (E°1 − E°2 ) −
log
−
log
a
b
n
n
[Ox1 ]
[Red 2 ]
a
a

0,0591
[
Ox1 ]
E1 − E 2 =  E°1 +
log
a
n
[
]
Red
1

0,0591
[
Ox1 ]
E1 = E°1 +
log
n
[Red 1 ]a
b
 
0,0591
[
Ox 2 ] 
 −  E° 2 +

log
b
 

n
[
]
Red
2
 

[
0,0591
Ox 2 ]
E 2 = E° 2 +
log
n
[Red 2 ]b
a
0,0591  [Ox1 ] 

E1 = E°1 +
log 
n
 [Red 1 ] 
b
b
a
0,0591  [Ox 2 ] 

E 2 = E° 2 +
log 
n
 [Red 2 ] 
b
[Ox1 ]
0,0591
E1 = E°1 +
log
[
Red 1 ]
n
 
a
[
Ox 2 ]
0,0591
log
E 2 = E°2 +
[
n
Red 2 ]
 
b
a n1 = b n2 = n
[
0,0591
Ox1 ]
E1 = E°1 +
log
[Red1 ]
n1
[
0,0591
Ox 2 ]
E 2 = E°2 +
log
[Red 2 ]
n2
Quindi, in generale, per la generica coppia RedOx:
il potenziale di riduzione attuale è:
Ox + ne– → Red
0,0591
[
Ox]
E = E° +
log
[Red ]
n e−
o ancor più in generale:
ν0xOx + ne– → νRedRed
dove
• n= numero di elettroni scambiati nella semireazione
• νOx coefficiente stechiometrico di Ox
• νRed coefficiente stechiometrico di Red
E = E°Ox/Red
a
0,0591
+
log 10
n
a
ν Ox
Ox
ν Red
Red
Come di solito, ai liquidi ed ai solidi puri assegniamo attività unitaria; per i
gas ammettiamo un comportamento ideale e, quindi, all’attività sostituiamo la
pressione; anche per le soluzioni ammettiamo un comportamento ideale e,
quindi, sostituiamo all’attività la concentrazione molare.
ν Ox
0,0591
[Ox]
E = E°Ox/Red +
log 10
ν Red
n
[Red]
Esempio di applicazione della legge di Nernst:
MnO4-(aq) + 8 H+(aq) + 5 e- → Mn2+(aq) + 4 H2O(l)
E MnO − /Mn 2+ = E°MnO − /Mn 2+
4
4
E MnO − /Mn 2+ = E°MnO − /Mn 2+
4
4
E MnO − /Mn 2+
4
E°°=1,491 V
a MnO − ⋅ a 8H +
0,0591
4
+
log10
5
a Mn 2+ ⋅ a 4H 2 O
= 1
0,0591
[MnO −4 ] ⋅ [ H + ]8
+
log 10
2+
5
[Mn ]
0,0591
[MnO 4− ] ⋅ [ H + ]8
= 1,491 +
log 10
2+
5
[Mn ]
Altri esempi di applicazione della legge di Nernst:
H+(aq) + e- → ½ H2(g)
E°= 0 V
[H + ]
[H + ]
E = 0 + 0,0591 ⋅ log 10 1/ 2 = 0,0591 ⋅ log 10 1/ 2
PH 2
PH 2
Cl2(g) + 2 e- → 2 Cl-(aq)
E°= + 1,358 V
PCl 2
0,0591
E = 1,358 +
log 10
2
[Cl − ]2
PbO2(s) + 4 H+(aq) + 2 e- → Pb2+(aq) + 2 H2O(l)
E°=1,460 V
0,0591
[H + ]4
E = 1,460 +
log 10
2
[Pb 2+ ]
NO3-(aq) + 3 e- + 4 H+(aq) → NO(g) + 2 H2O(l)
[NO 3− ][H + ]4
0,0591
E = 0,960 +
log10
3
PNO
E°= + 0,960 V
Un’altra utilità della legge di Nernst:
∆G° == −nF ∆E°
Nota la differenza di potenziale tra due
coppie coniugate redox è possibile
prevedere la variazione di energia libera
–∆
∆G°= RT ln K
∆G°/RT
K = e –∆
K = e nF∆∆E°/RT
sostituendo i valori delle costanti e passando dalla base naturale a quella decimale:
K = 10
n∆E °
0,0591
ove
n = m.c.m.
della reazione (globale) redox
Nota la differenza di potenziale standard tra due coppie coniugate
redox è possibile prevedere la condizione di equilibrio, cioè è possibile
calcolare la costante (K) termodinamica di equilibrio.
Tipi di elettrodi (semielementi)
Elettrodi di 1a SPECIE: se entrambe le forme (ossidata e
ridotta) della coppia redox, o almeno una di essa sono in soluzione.
Il potenziale attuale (E) di un tale elettrodo dipende dalla
concentrazione di entrambe le forme (o almeno da una delle due).
Elettrodi di 2a SPECIE: se entrambe le forme (ossidata e
ridotta) della coppia redox sono un solido oppure un liquido
insolubile; quasi tutte le coppie che vengono usate per questi
elettrodi sono costituite da un metallo (M), un suo sale poco
solubile (MmAn) e l’anione (Am-) di quest’ultimo introdotto in
soluzione da un elettrolita forte solubile. Il potenziale attuale (E)
di un tale elettrodo dipende dalla concentrazione dell’anione Anpoiché le concentrazioni (attività) di solidi puri o liquidi puri sono
poste per convenzione unitarie.
Elettrodi di 1a specie:
Un elettrodo è di prima specie se entrambe le
forme (ossidata e ridotta) della coppia redox, o
almeno una di esse, sono in soluzione.
Esempio, coppia redox costituita da un metallo e dai suoi ioni:
M
n+
(aq)
EM
n+
−
+ ne → M (s)
/M
= E° M
n+
/M
0,0591
n+
+
⋅ log [M ]
n
Elettrodi di 1a specie:
Un elettrodo è di prima specie se entrambe le
forme (ossidata e ridotta) della coppia redox, o
almeno una di esse, sono in soluzione.
Esempio, coppia redox che presenta sia la forma ossidata che quella
ridotta in soluzione:
Fe
3+
(aq)
−
+ e → Fe
2+
(aq)
E Fe3+ / Fe 2+ = E°Fe3+ / Fe 2+
Pt
2+
3+
Fe (C Fe 2+ ), Fe (C Fe3+ )
3+
0,0591
[Fe ]
+
⋅ log
1
[Fe2+ ]
Altri esempi di elettrodi di 1a specie: gli elettrodi a gas
possiamo considerarli come elettrodi di prima specie
Pt
H +(aq) + e - →
1
H 2 (g)
2
E° = 0 V
(P in atm) H 2 (g) H + (C H + )
[H + ]
[H + ]
E = E° + 0,0591 ⋅ log 10 1 / 2 = 0,0591 ⋅ log 10 1 / 2
PH 2
PH 2
1
2
Cl2(g) + e - → Cl-(aq)
E = E° + 0,0591 ⋅ log 10
1
2
Pt
E° = 1,358 V
(P in atm) Cl2 (g) Cl− (CCl − )
PCl1 22
−
[Cl ]
O 2 + 2 H + + 2 e – → H 2O
= 1,358 + 0,0591 ⋅ log 10
E° = 1,229
PCl1 22
[Cl − ]
Pt
(P in atm) O2 (g) H + (C H + )
0,0591
0,0591
12
+ 2
⋅ log PO 2 ⋅ [H ] = 1,229 +
⋅ log PO1 22 ⋅ [H + ]2
E = E° +
2
2
Elettrodi di 2a specie
Un elettrodo è di seconda specie se sia la forma ossidata che quella
ridotta è un solido insolubile; quasi tutte le coppie che vengono usate
per questi elettrodi sono costituite da un metallo (M), un suo sale
poco solubile (MmAn) e l’anione (Am-) di quest’ultimo introdotto in
soluzione da un elettrolita forte solubile.
Esempio 1: l’elettrodo ad argentoargento-argento cloruro
−
AgCl (s) + e → Ag (s) + Cl
E AgCl/Ag,Cl − = E°AgCl/Ag,Cl −
Ag
−
(aq)
0,0591
1
+
⋅ log
1
[Cl− ]
AgCl (s) Cl− (C Cl − )
−
E AgCl/Ag,Cl − = 0,222 − 0,0591 ⋅ log [Cl ]
In una soluzione satura di KCl:
E AgCl/Ag,Cl − = 0,198 V
Esempio 1: l’elettrodo ad argentoargento-argento cloruro
Ag
AgCl (s) Cl− (C Cl − )
Dato che il potenziale varia
al variare della
concentrazione di KCl (cioè
Cl-), questa deve essere nota
(solitamente soluzione
satura circa 4,6M)
Elettrodi di 2a specie
Esempio 2: l’elettrodo a calomelano
1
2
−
Hg 2Cl2 (s) + e → Hg (s) + Cl
E Hg Cl
2
2 /Hg,Cl
E Hg Cl
2
-
= E°Hg Cl
2
−
(aq)
2 /Hg,Cl
-
Hg
−
Hg 2Cl2 (s) Cl (C Cl − )
0,0591
1
+
⋅ log
1
[Cl− ]
−
2 /Hg,Cl
= 0,268 − 0,0591 ⋅ log [Cl ]
In una soluzione satura di KCl:
E Hg Cl
2
2 /Hg,Cl
-
= 0,244 V
Esempio 2: l’elettrodo a calomelano
Nelle misure potenziometriche raramente è utilizzato un elettrodo a idrogeno
(difficoltà operative). Un elettrodo di riferimento ideale deve avere un potenziale
noto, costante e indipendente dalla soluzione da analizzare. Un elettrodo di
riferimento ideale deve inoltre essere robusto e facile da assemblare.
Hg
Hg 2Cl2 (s) Cl− (C Cl − )
Ponte salino nelle pile con un elettrodo di 2a specie
In una pila con entrambi gli elettrodi di seconda specie, la forma
ossidata della coppia ossidante e quella ridotta della coppia riducente,
entrambe solide e confinate ai due elettrodi, non possono venire a
contatto diretto tra loro: in questi casi non è, quindi, necessario il
ponte salino per separare fisicamente le due semicelle.
Se dei due elettrodi uno è di seconda specie e l’altro di prima, invece, il
ponte salino può essere necessario o inutile: ciò dipende dalla
possibilità, legata al loro stato fisico, che la forma ossidata della
coppia ossidante e quella ridotta della coppia riducente vengano o meno
a contatto tra loro e si scambino direttamente gli elettroni mettendo in
corto circuito la pila. Per verificare quale delle due circostanze si
verifica e, quindi, per determinare se occorre o meno usare il ponte
salino, bisogna scrivere la reazione di ossidoriduzione nella direzione in
cui avviene spontaneamente, partendo dai potenziali delle due coppie.
Ponte salino nelle pile con un elettrodo di 2a specie
Esempio 1.
Pila costruita con le coppie
H+/H2 (E° = 0,000 V)
AgCl / Ag, Cl- (E° = 0,222 V)
−
(+) AgCl (s) + e − → Ag (s) + Cl(aq)
1
(−
−)
H 2 (g) → H + (aq) + e −
2
1
−
+
+ H (aq)
AgCl (s) + H 2 (g) → Ag (s) + Cl(aq)
2
Pt (−)
H 2 (g) (PH 2 = 1 atm ) H + (pH = 0)
Ponte salino
NON
NECESSARIO
Ag (+)
−
Cl(aq)
(1,0 M) AgCl (s)
Ponte salino nelle pile con un elettrodo di 2a specie
Esempio 2.
Pila costruita con le coppie
H+/H2 (E° = 0,00 V)
AgI / Ag, I- (E° = -0,15 V)
(−
−)
−
Ag (s) + I (aq)
→ AgI (s) + e −
(+
+)
1
H (aq) + e → H 2 (g)
2
+
−
Ag (s) + I
−
(aq)
+ H
+
(aq)
I
−
(aq)
1
→ AgI (s) + H 2 (g)
2
Pt (+)
Ag (−)
AgI (s)
Ponte salino
NECESSARIO
(1,0 M)
H + (pH = 0) H 2 (g) (PH 2 = 1 atm)
Noi,tuttavia, considereremo sempre l’uso del
ponte salino nei nostri esercizi
esercizi..
Un caso particolare: Pile di concentrazione
(+)
M n + (s) + n e − → M (s)
E C = E° M n+ /M +
( −)
[ ]
0,0591
0,0591
⋅ log M n + = E° M n+ /M +
⋅ log C1
n
n
M (s) → M n + (s) + n e −
E A = E° M n + /M +
M (−)
M n + (C 2 )
[
]
0,0591
0,0591
⋅ log M n + = E° M n + /M +
⋅ log C 2
n
n
M (+)
M n+ (C1 )
∆E = E C − E A = E°M n+ /M +
0,0591
0,0591
C

 0,0591
⋅ log C1 −  E°M n+ /M +
⋅ log C 2  =
⋅ log 1
n
n
n
C2


0,0591
C1
∆E = E C − E A =
⋅ log
n
C2
Le pile di concentrazione, ad esempio:
0,059
E = Eo +
log10 [ Ag + ]
1
[ Ag + ]1
C1
∆E = 0,0591 ⋅ log10
= 0,0591 ⋅ log10
+
C2
[ Ag ] 2
C1 = C2 pila scarica
C1 > C2 catodo a destra
C1 < C2 catodo a sinistra
Un particolare esempio: pila di concentrazione con elettrodi ad
idrogeno in cui [H+]1> [H+]2 (vale a dire pH1 < pH2)
Il pH-metro
• Il pH-metro misura il
pH di una soluzione
usando un elettrodo che
risponde
alla
concentrazione di H+.
• L’elettrodo produce un
voltaggio proporzionale
alla conc. di H+.
• Il
voltaggio
viene
convertito in misura di
Deve essere calibrato prima
pH su un display.
dell’uso utilizzando soluzioni
standard a pH noto (vale a
dire: soluzioni tampone).
Il pH-metro
Esercitazione
Dal libro Nobile-Mastrorili, oltre agli esercizi svolti e
commentati, potete risolvere gli esercizi:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15
alle pagine 617-621
N.B. Per la risoluzione degli esercizi del libro Nobile-Mastrorili utilizzare anche i
dati riportati nella tabella 16.1. Si considerino i volumi additivi e le pressioni dei
gas che gorgogliano sugli elettrodi pari a 1 atm.
Infine svolgere gli esercizi riassuntivi e integrativi
riportati alla fine di questa lezione. Considerare i volumi additivi
invece le pressioni dei gas che gorgogliano sugli elettrodi sono indicate volta
per volta. I potenziali standard sono indicati esercizio per esercizio
Esercizio N.2 di pagina 617
Anodo:
E A = E° Fe 2 +
Catodo:
E°Fe 2+
Fe → Fe 2 + + 2e −
+
Fe
[
= −0,447 V
Fe
]
0,0591
0,0591
log 10 Fe 2+ = −0,447 +
log 10 [0,20] = −0,468 V
2
2
−
IO3 + 4e − + 2H 2O → IO− + 4OH − E° IO − ,OH−
= 0,15 V
IO3-
−
[IO 3 ]
0,0591
0,0591
0,8
E C = E° +
log 10
=
0,15
+
log
= 0,168 V
10
−
− 4
4
4
4
[IO ] ⋅ [OH ]
(0,8) ⋅ (0,5)
fem = ∆E = E C − E A = 0,168 − (−0,468) = +0,636 V
Fe → Fe 2 + + 2e −
×2
IO 3 + 4e - + 2H 2 O → IO - + 4OH −
-
2Fe + IO 3 + 2H 2 O → 2Fe 2+ + IO - + 4OH −
-
Esercizio N.3 di pagina 618
Prima di disegnare lo schema della pila vediamo dall’equazione di Nernst quale
semielemento si comporta da anodo o da catodo:
2H + + 2e − → H 2
E° H +
=0V
H2
[ ]
0,0591
[H + ]2 0,0591
10−3
E =0+
log 10
=
log 10
2
PH 2
2
1
Hg 2Cl 2 + 2 e – → 2 Hg + 2 Cl –
Quindi:
anodo (-) :
catodo (+ ) :
E° Hg Cl
2
2
2
0,0591
=
⋅ (−6) ≅ −0,177 V
2
= +0,268 V ≡ E attuale
Hg,Cl -
H 2 → 2H + + 2e −
Hg 2 Cl 2 + 2 e – → 2 Hg + 2 Cl –
E A = −0,177 V
E C = +0,268 V
reazione complessiva : H 2 + Hg 2 Cl 2 → 2H + + 2 Hg + 2 Cl –
fem = ∆E = E C − E A = 0,268 − ( −0,177) = +0,445 V
….prosieguo dell’esercizio N.3 di pagina 618
Lo schema della pila:
Non è necessario il ponte salino (||) perché la specie ridotta (H2) della
coppia riducente non viene a contatto con la forma ossidata della coppia
ossidante (Hg2Cl2):
+
H 2 + Hg 2Cl 2 → 2H + 2 Hg + 2 Cl
Esercizio simile il N.7 di pagina 619
Noi,tuttavia, considereremo sempre l’uso
del ponte salino nei nostri esercizi
esercizi..
–
Esercizio N.10 di pagina 619
H+
−
3
−
IO + H 2 O 2 → I + O 2
E° IO − /I- = 1,085 V E°O 2 /H2O 2 = 0,695 V
3
(-) H 2 O 2 → O 2 + 2H + + 2e −
×3
mcm = 6 = n
(+) IO3− + 6e − + 6H + → I − + 3H 2 O
−
3
−
IO + 3H 2 O 2 → I + 3O 2 + 3H 2 O K = 10
K = 10
n∆E °
0,0591
= 10
6⋅(1, 085− 0 , 695)
0 , 0591
= 10
6⋅0 , 39
0 , 0591
n∆E °
0,0591
= 10 +39,594 ≅ 3,92 ⋅10 +39
….prosieguo dell’esercizio N.10 di pagina 575
Lo schema della pila:
0,0591
PO2 ⋅ [H + ]2
0,0591
1 ⋅ [0,10]
+
log 10
= 0,695 +
log 10
= 0,665 V
2
[H 2 O 2 ]
2
[0,10]
2
E A = E°O 2 /H2O 2
E C = E°IO − /I3
−
[IO 3 ] ⋅ [H + ]6
0,0591
0,0591
[0,10] ⋅ [0,10]6
+
log 10
= 1,085 +
log 10
= 1,026 V
−
6
[I ]
6
[0,10]
fem = ∆E = E C − E A = 1,026 − 0,665 = +0,361 V
Esercizi sulle applicazioni dell’equazione di Nernst
Usando l’equazione di Nernst è possibile da misure di f.e.m. delle pile
risalire alle concentrazioni di specie in soluzione. Questo approccio è
particolarmente utile quando si tratta di determinare concentrazioni
particolarmente basse come nel caso della misura del pH o della
solubilità di sali poco solubili.
Misure di pH
Supponiamo di avere una soluzione acquosa di cui si voglia misurare il
pH: a tale scopo si costruisce una cella voltaica costituita da un
elettrodo ad idrogeno in cui una barra di platino è immersa nella
soluzione di cui si vuole misurare il pH e in cui gorgoglia H2 gassoso ad
1 atmosfera ed un altro elettrodo quale ad esempio l’elettrodo
standard di zinco
Zn(-)
Pt(+)
|Zn2+(aq)(1M)||H+(aq)([H+] incognita)|H2(1atm)
La f.e.m. di questa pila dipende dalle concentrazioni degli
ioni H+ tramite l’equazione di Nernst
∆E = E + − E − = EH0 2
0,0591
[H + ]2
0,0591
0
+
⋅ log 10
− EZn −
⋅ log 10 [Zn + + ]
2
PH 2
2
in cui:
E 0H 2 = 0 V
E 0Zn = − 0,76 V PH 2 = 1 atm
[Zn + + ] = 1,0 M
si ha, quindi,
0,0591
[H + ]2
0,0591
∆E = 0 +
⋅ log 10
+ 0,76 −
⋅ log 10 1
2
1
2
da cui si ricava
0,76 − ∆E
pH =
0,0591
Determinazione del Ks
Lo stesso principio permette di determinare la concentrazione di uno
ione implicato in un equilibrio di solubilità in una opportuna soluzione
satura del sale poco solubile (in genere in acqua pura o in una
soluzione a concentrazione nota dell’altro ione) e da questa risalire
poi al Ks. Generalmente si fa uso di pile di concentrazione che
semplificano l’equazione di Nernst.
Esempio – Determinare il Ks di AgCl sapendo che la f.e.m. della
seguente pila
Ag(-)
Ag(+)
AgCl | Cl-(1M) || Ag+(aq)(1M) |
, è di 0,58V a 25°C.
La “reazione” di cella è
Ag+(aq)(1M) → Ag+(aq)(incogn.)
, in cui Ag+(incogn.) è la concentrazione di ioni Ag+ nella soluzione
satura di AgCl(s) contenente Cl- 1M.
[Ag + ]+
1
∆E = 0,0591 ⋅ log 10
= 0,0591 ⋅ log 10
+
+
[Ag ]−
[Ag ]−
+
0,58 = −0.0591 ⋅ log 10[Ag ]−
+
[Ag ] = 10
− 9,80
= 1,58 ×10
+
log 10 [Ag ]− = −9,80
−10
Dall’espressione per Ks
AgCl(s)
Ag+(aq) + Cl-(aq)
K s = [Ag + ] ⋅ [Cl − ]
, segue
K s = (1,58 ⋅10
−10
) ⋅ (1) = 1,58 ⋅10
−10
 mol 
 L 
2
Esercizio riassuntivo
Determinare la costante di dissociazione Ka dell’ acido formico HCOOH
sapendo che la f.e.m. della pila schematizzata di seguito è 0,358V e che il
potenziale standard dell’elettrodo a cloruro di argento è 0,222 V:
Ag( + )
Pt(-)
H 2(g)(1atm) [HCOOH] = 0,14 M
[Cl - ] = 1,0 M AgCl (s)
+ 2
1
0,0591
[H
]
0
0
∆E = E + − E − = E AgCl,Cl − /Ag + 0,0591⋅ log − − E H + /H −
⋅ log
2
[Cl ]
2
PH 2
0,358V
0,222 V
1
0,358 − 0,222
log x = −
0,0591
0,0591
0,358 = 0,222 −
⋅ 2 ⋅ log x
2
x = [H + ] ≡ [H 3O + ] = 10
−
0,358−0,222
0,0591
= 10 −2,30 = 5,0 ⋅10 −3 M
x
HCOOH(aq) + H2O(l) ⇄ HCOO- (aq) + H3O+ (aq)
(i)
(eq)
0,14
0,14-x
--x
~0
x
[HCOO − ] ⋅ [H 3O + ]
x2
(5 ⋅10 −3 ) 2
Ka =
=
=
=
−3
[HCOOH]
0,14 − x 0,14 − 5 ⋅10
(5 ⋅10 −3 ) 2
2,5 ⋅10 −5
−4
Ka =
1,85
10
=
≅
⋅
−3
0,14 − 5 ⋅10
0,135
 mol 
 L 
Esercizio riassuntivo
Calcolare KS a 25°C del AgBrO3, essendo noto che a questa temperatura, la
f.e.m. della pila:
Ag(-)
Ag(+)
| soluzione satura di AgBrO3 || Ag+(0,0734M) |
è uguale a 0,066 V.
[Ag + ]+
0,0734
∆E = 0,066 = 0,0591 ⋅ log
=
0,0591
⋅
log
[Ag + ]−
[Ag + ]−
log
0,0734 0,066
0,0734
=
⇔
= 10
+
+
[Ag ]− 0,0591
[Ag ]−
0,066
0,0591
⇒ [Ag + ]− =
0,0734
10
0,066
0,0591
= 5,61⋅10 −3 M
+
−
AgBrO 3(s) →
← Ag ( aq ) + BrO 3 ( aq )
S
+
S
−
(
K S = [Ag ] ⋅ [BrO 3 ] = S = 5,61⋅10
2
)
−3 2
= 3,14 ⋅10 −5 M 2
Esercizio (riassuntivo) N.12 di pagina 620
Questa non è altro che una pila di concentrazione al [Ag+]:
Ag + (aq ) + e − → Ag(s)
[Ag + ]1
[Ag + ] +
∆E = 0,0591 ⋅ log
= 0,0591 ⋅ log
= E+ − E+
+
[Ag ] 2
[Ag ]Adesso dobbiamo capire quale
semielemento è il catodo (C+:
ovvero concentrazione maggiore
per Ag+)
La traccia dell’esercizio
ammette implicitamente che vi
sarà precipitazione del Ag2CrO4
2AgNO 3 ( aq) + Na 2 CrO 4 (aq ) → Ag 2 CrO 4 ( s ) + 2NaNO 3 (aq )
i)
c)
f)
tot)
Volume finale = 2,0 L ⇔ [CrO 24− ] =
Ag 2 CrO 4 ( s )
→
←
2Ag + ( aq ) + CrO -24 ( aq )
2S
0,3 + S
0,2
0,2
0
0,7
0,1
0,6
0,1
0,1
0,2
0,2
0,6 mol
= 0,3 M
2,0 L
⇒ K S = [Ag + ]2 ⋅ [CrO -24 ] = ?
S << 0,3
[Ag + ] = 2S
K S = [Ag + ]2 ⋅ [CrO -4 ] = [2S]2 ⋅ 0,3
….prosieguo dell’esercizio N.12 di pagina 620
A questo punto è chiaro che il catodo è quello dove è presente la soluzione
0,1 M di AgNO3
[Ag + ]1
[Ag + ] +
0,1
∆E = 0,0591 ⋅ log
=
0,0591
⋅
log
=
0,0591
⋅
log
2S
[Ag + ] 2
[Ag + ]-
0,1
0,278 = 0,0591 ⋅ log
2S
0,278
0,1
 0,1 
= log
⇔ 
 = 10
0,0591
2s
 2S 
+ 2
0,278
0,0591
⇒ 2S =
10
[
K S = [Ag ] ⋅ [CrO ] = [2S] ⋅ 0,3 = 1,977 ⋅ 10
4
2
0,1
0,278
0,0591
= 1,977 ⋅ 10 −6
] ⋅ 0,3 ≅ 1,17 ⋅10
−6 2
−12
M3
Esercizio riassuntivo
Per la seguente pila a 25°C:
Pt
Cl2(g)
(1 atm)
Pt
ClO3- (1·10-3 M)
MnO4- (1·10-3 M)
H+ (1·10-1 M)
H+ (? M)
Mn2+ (1·10-1 M)
Calcolare a quale pH dell’elettrodo di destra la pila risulta scarica (f.e.m.=0)
sapendo che, per le coppie ClO3-,H+/Cl2 e MnO4−,H+/Mn2+, i potenziali standard di
riduzione valgono, rispettivamente, 1,470 V e 1,507 V.
Svolgimento:
f.e.m. = 0
⇔
f.e.m. = E sinistra − E destra = E destra − E sinistra = 0
⇒
E sinistra = E destra
È indifferente scegliere il polo di destra o sinistra come anodo o catodo.
La semireazione a sinistra scritta nel senso della riduzione è
( +5)
−
3
−
(0)
+
2 Cl O + 10 e + 12 H → Cl 2 + 6 H 2 O
da cui il potenziale è ricavabile mediante l’equazione di Nernst:
E sinistra
[
] [ ]
2
0,0591
ClO3− ⋅ H +
log
= E° ClO− ,H + /Cl +
3
2
10
PCl2
= 1,470 +
[
]
12
[
]
0,0591
1⋅10 −3 ⋅ [0,1]
log
= 1,470 +
10
1
0,0591
0,0591
log 1⋅10 −18 = 1,470 +
⋅ (− 18)
10
10
2
12
=
La semireazione a destra scritta anch’essa nel senso della riduzione è
( +7)
−
4
−
+
( +2)
Mn O + 5 e + 8 H → M n + + + 4 H 2 O
e permette di impostare l’equazione di Nernst così:
E destra
[
][ ]
[ ]
0,0591  MnO 4− ⋅ H +
= E° MnO− ,H + /Mn ++ +
log
4

5
Mn + +

= 1,507 +
E sinistra
([
][ ] )
0,0591
log 1 ⋅10 − 2 ⋅ H +
5
= E destra
1,470 +
8
[
][ ]

 1 ⋅10 −3 ⋅ H +
0,0591
 = 1,507 +
log


5
[0,1]


0,0591
8
= 1,507 +
⋅ (− 2 ) + 0,0591⋅ log H +
5
5
8
[ ]
[ ]
0,0591
0,0591
8
⋅ (− 18) = 1,507 +
⋅ (− 2 ) + 0,0591 ⋅ log H +
10
5
5
[ ]
14,70 − 1,0638 = 15,07 − 0,2364 + 0,9456 ⋅ log H +
[ ]
log H + =
− 1,1974
≅ −1,267
0,9456
pH ≅ 1,27
⇔
[H ] = 10
+
−1,267
≅ 0,0542 M
8

=


Esercizio riassuntivo (simile)
Sapendo che, per le coppie Co3+/Co2+ e MnO4−,H+/Mn2+, i potenziali standard
di riduzione valgono, rispettivamente 1,30 V e 1,51 V, stabilire per quale
valore del pH è nulla la forza elettromotrice (f.e.m.) della seguente pila:
Pt
Pt
3+
-3
-
-3
Co (1·10 M)
MnO4 (1·10 M)
Co2+ (1·10-1 M)
H (? M)
+
2+
-1
Mn (1·10 M)
Prova tu!!
Risultato: pH=3,22
Esercizio riassuntivo
Sapendo che la costante di dissociazione dell'ammoniaca vale Kb=1,810-5M e
che il potenziale standard di riduzione della coppia O2/OH− vale E0= 0,40 V,
calcolare la fem della pila: Pt
Pt
H2(g)
P = 1 atm
NH4Cl
-3
(1·10 M)
-4
NH4Cl (5·10 M)
NH3 (1,5·10-3 M)
O2(g)
P = 1 atm
e il pH delle due soluzioni elettrodiche.
Svolgimento:
Semielemento di sinistra:
NH4+(aq) + H2O(l) ⇄ NH3(aq) + H3O+(aq)
CS
--~0
NH4Cl(aq) →NH4+(aq)+ Cl−(aq)
CS – x
x
x
K W [NH 3 ] [H 3O + ]
costante d' idrolisi = K i = K a =
=
Kb
[NH 4+ ]
−14
K W 1,0 ⋅10
x
−10
=
= 5,56 ⋅10 =
−5
K b 1,8 ⋅10
(CS − x)
2
Cs
1 ⋅10 −3
=
> 380 ⇒
−10
K a 5,56 ⋅10
C S − x ≅ CS
[H 3O + ]2
Ka =
CS
[H 3O + ] = K a ⋅ CS = 5,56 ⋅10 −10 ⋅1 ⋅10 −3 = 7,45 ⋅10 −7 M ≡ [H + ]
pH = −log 10[H 3O + ] = −log 10[7,45 ⋅10 −7 ] ≅ +6,13
2 H + (aq) + 2e − → H 2 (g)
E sinistra = E 0H + /H2
0,0591
[H + ]2
0,0591
[7,45 ⋅10 −7 ]2
+
log
= 0+
log
= −0,362 V
2
PH 2
2
1
Semielemento di destra:
[OH − ] = K b ⋅
C b 1,5 ⋅10 −3 M
0,1 <
=
= 3 < 10 ⇒ tampone
−4
Cs
5 ⋅10 M
Cb −x
C
≅ Kb ⋅ b
Cs + x
Cs
⇒ [H 3O + ] =
KW
C
Kb ⋅ b
Cs
K W Cs
1 ⋅10 −14 5 ⋅10 − 4
−10
[H 3O ] =
⋅
=
⋅
=
1,852
⋅
10
M
−5
−3
K b C b 1,8 ⋅10 1,5 ⋅10
+
(
)
pH = −log 1,852 ⋅10 −10 ≅ +9,73
O 2 (g) + 4e − + 2 H 2 O → 4 OH −
E destra
PO 2
0,0591
0,0591
[H + ]4
= E° +
⋅ log
⋅ = 0,40 +
⋅ log
=
− 4
4
4
[OH ]
4
[KW ]
0,0591
[1,852 ⋅10 −10 ]4
= 0,40 +
⋅ log
= 0,652 V
−14 4
4
[1 ⋅10 ]
E destra = 0,652 V
E sinistra = −0,362 V
Catodo (+)
Anodo (-)
O 2 (g) + 4e − + 2 H 2 O → 4 OH −
H 2 (g) → 2 H + (aq) + 2e −
2 H 2 (g) + O 2 (g) → 2 H 2O
fem = E destra − E sinistra = E + − E − = 0,652 V − (− 0,362 V ) = +1,014 V
x 2
Esercizio riassuntivo
Assegnata la seguente pila a 25°C:
Pt (+)
[MnO4-]=0,1 M
[Mn++] = 0,1 M
[H+] = 0,001 M
Ag (-)
Ag3PO4
soluzione satura
calcolarne la f.e.m. sapendo che i potenziali standard di riduzione del
catodo ( E° MnO −4 ,H + /Mn ++ ) e delll’anodo ( E° Ag+ /Ag ) valgono rispettivamente
1,507 V e 0,800 V e che il prodotto di solubilità (KS) del Ag3PO4 a 25°C è
uguale a 8,88·10–17 (mol/L)4.
Svolgimento:
Semielemento di sinistra (catodo +):
E + = E°MnO− ,H + /Mn 2+
4
MnO 4− + 5e − + 8H + → Mn 2+ + 4H 2O
0,0591
[MnO 4− ] ⋅ [H + ]8
0,0591
0,1⋅ [0,001]8
+
log
= 1,507 +
log
≅ 1,223 V
2+
5
[Mn ]
5
[0,1]
Semielemento di destra (anodo -):
Ag → Ag + + e -
E − = E° Ag + /Ag + 0,0591 ⋅ log[Ag + ] = 0,800 + 0,0591 ⋅ log[Ag + ]
[Ag + ] = ?
Ag 3 PO 4 (s)
+
3 Ag (aq)
+ PO34− (aq)
3S
S
K s = [ Ag + ]3 ⋅ [PO 34- ] = 8,88·10–17 (mol/L) 4
K S = [3S] ⋅ [S] = 27S4
3
Nota bene:
–17
K
8,88·10
⇒S=4 S =4
= 4,258·10– 5 M
27
27
[Ag + ] = 3 S = 3 ⋅ 4,258·10–4 M
E − = 0,800 + 0,0591⋅ log[3 ⋅ 4,258·10–5 ] ≅ 0,570 V
fem = ∆E = E + − E − = 1,223 V − 0,570 V = 0,653 V
Esercizio riassuntivo (effetto delle pressioni sugli elettrodi)
La pila:
Pt (-)
H2(g)
P= 2 atm
Pt (+)
[HA] = 1,0 M
[HCl]=1·10-4 M
H2
P= 1 atm
ha una fem pari a 0,068V a 25°C. Determinare il pH della soluzione di HA e
la costante di equilibrio dell’acido.
Svolgimento:
∆E = E + − E − = E 0H 2 + 0,0591⋅ log
[H + ]+
PHcatodo
2


+
[H
]
- 
−  E 0H 2 + 0,0591⋅ log
anodo 


P
H
2


anodo 

+
P
[H ]+
[H ][H ]+
H2

∆E = 0,0591 ⋅ log
− 0,0591 ⋅ log
= 0,0591 ⋅ log 
⋅
+

catodo
anodo
catodo
[H
]

PH 2
PH 2
P
 H2

anodo 
 [H + ]
−4
P

⋅
1
10
2
H


2
+

fem = 0,068 = ∆E = 0,0591⋅ log 
⋅
= 0,0591⋅ log 
⋅ +
+

catodo
[H ]- 
[H ] PH
 1
2


+
+
calcolare




 1 ⋅10 −4 ⋅ 2 
0,068

= log 

0,0591
x


 1 ⋅10 −4 2 

⋅
0,068 = 0,0591 ⋅ log 
x 
 1
 2 ⋅10 −4 

1,1506 = log 

x


(
1,1506 = log
(
)
2 ⋅10 −4 − log x
)
log x = log 2 ⋅10 −4 − 1,1506 = −3,8495 − 1,1506 = 5,0001
x = [H + ] = [H 3O + ] = 10 −5, 0001 ≅ 1 ⋅10 −5 M
pH = 5
HA(aq) + H2O(l) ⇄ A− (aq) + H3O+ (aq)
(i)
(eq)
1,0
1,0-x
x
x
[A − ] ⋅ [H 3O + ]
x2
(1 ⋅10 −5 ) 2
Ka =
=
=
=
−5
[HA]
1 − x 1 − 1 ⋅10
(1 ⋅10 −5 ) 2
−10
Ka =
≅
1
⋅
10
[mol/l]
−5
1 − 1⋅10
Esercizio riassuntivo (effetto delle pressioni sugli elettrodi)
La forza elettromotrice (f.e.m.) della seguente pila:
Pt (+)
Ag (-)
Cl2(g)+Ne(g)
PTOT= 1atm [HCl] = 0,01 M [AgNO ]=0,10 M
3
vale ∆E= 0,735V a 25,0°C. Sapendo che E0Ag+/Ag= 0,800V e E0Cl2/Cl=1,360V, si calcoli la frazione molare di Ne nella miscela gassosa che
gorgoglia sull'elettrodo di platino. [χ
χNe=0,164]
Svolgimento:
Semielemento di sinistra (catodo +): Cl2 + 2e − → 2Cl−
[Cl− ] ≡ [HCl] = 0,01 M
E + = E°Cl /Cl− +
2
PCl 2
PCl 2
0,0591
0,0591
log
1
,
360
log
=
+
2
[Cl − ]2
2
[0,01]2
Semielemento di destra (anodo -):
Ag → Ag + + e -
[Ag + ] ≡ [AgNO 3 ] = 0,1 M
E − = E° Ag + /Ag + 0,0591 ⋅ log[Ag + ] = 0,800 + 0,0591 ⋅ log[ 0,1]
fem = 0,735V = ∆E = E + − E PCl 2
0,0591
0,735 = 1,360 +
log
− (0,800 + 0,0591⋅ log[ 0,1])
2
2
[0,01]
( )
0,0591
0,0591
0,735 = 1,360 +
log PCl 2 −
log[ 0,01]2 − 0,800 − 0,0591 ⋅ log[ 0,1]
2
2
( )
0,0591
0,735 = 1,360 +
log PCl 2 + 0,1182 − 0,800 + 0,0591
2
0,0591
log PCl 2 = 0,735 − 1,360 − 0,1182 + 0,800 − 0,0591 = −0,0023
2
0,0023⋅2
−
0,0023 ⋅ 2
log PCl 2 = −
⇒ PCl 2 = 10 0, 0591 ≅ 0,836 atm
0,0591
( )
( )
χ Ne
PNe PTOT - PCl 2 1 atm - 0,836 atm
=
=
=
= 0,164
PTOT
PTOT
1 atm
Esercizio riassuntivo
Determinare di quanto varia la f.e.m. della pila:
Fe
Ag
| [Fe+2]=5,0·10-2 M | | Ag2CrO4 sol. satura |
se nel semielemento di destra, il cui volume è 0,5 litri, si aggiungono 81 mg di
Na2CrO4 solido (elettrolita forte e completamente solubile). Sono noti i valori
dei potenziali standard di riduzione delle coppie Fe+2/Fe e Ag+/Ag (-0,44 V e
+ 0,80 V) e quello del prodotto di solubilità di Ag2CrO4 (9·10-12 M3 ).
[R. ∆fem=∆
∆E2-∆
∆E1=-0,025 V]
Svolgimento:
Semielemento di sinistra:
E sinistra = E° Fe 2+ /Fe +
Fe 2 + + 2e − → Fe
0,0591
0,0591
log[Fe 2 + ] = −0,44 +
log[ 5 ⋅10 − 2 ] ≅ -0,478 V
2
2
È molto probabile (quasi certo) che sia l’anodo (ossidazione):
Fe → Fe 2+ + 2e −
Ag + + e − → Ag
Semielemento di destra
?
E destra = E° Ag + /Ag + 0,0591 ⋅ log[Ag + ] = 0,800 + 0,0591 ⋅ log[Ag + ]
Prima dell’aggiunta
Ag 2CrO 4 (s)
2 Ag
+
(aq)
2S
+ CrO
S
2−
4 (aq)
K S = [Ag + ]2 ⋅ [CrO 24− ] = 9 ⋅10−12 M 3
[Ag + ] = 2S
−12
9
⋅
10
K S = [2S]2 ⋅ [S] = 9 ⋅10 −12 ⇒ S = 3
= 1,31⋅10 − 4 M
4
[Ag + ] = 2 ⋅1,31⋅10−4 M = 2,62 ⋅10−4 M
E destra = 0,800 + 0,0591 ⋅ log[2,62 ⋅10 −4 ] ≅ 0,588V
È il catodo (riduzione):
Ag + + e − → Ag
fem = E destra − E sinistra = ∆E1 = 0,588 − (− 0,478 ) = 1,066 V
81 mg di Na2CrO4 solido aggiunto in 0,5 litri
n Na 2CrO 4 =
[CrO ] =
24
n CrO 24
V
Ag 2CrO 4 (s)
i)
m Na 2CrO 4
PM Na 2CrO 4
0,081 g
≅ 5 ⋅10 −4 mol ≡ n CrO 24
161,9732(g/mol )
5 ⋅10 −4 mol
=
= 1 ⋅10 −3 M
0,5 L
+
2 Ag (aq)
+ CrO 24− (aq)
--
eq)
=
2S
1·10-3
1·10-3+S
K S = [2S]2 ⋅ [0,001] = 9 ⋅10 −12
K S = [Ag + ]2 ⋅ [CrO24− ] = 9 ⋅10−12 M 3
[Ag + ] = 2S
S < 0,001 ⇒ 0,001 + S ≈ 0,001
9 ⋅10 −12
⇒S=
= 4,743 ⋅10 −5 M
4 ⋅ 0,001
[Ag + ] = 2 ⋅ 4,743 ⋅10−5 M = 9,486 ⋅10−5 M
E destra = 0,800 + 0,0591 ⋅ log[9,486 ⋅10 −5 ] ≅ 0,563 V
Ag + + e − → Ag
fem = E destra − E sinistra = ∆E 2 = 0,563 − (− 0,478 ) = 1,041 V
È ancora ancora il catodo (riduzione):
∆fem = ∆E 2 − ∆E1 = 1,041 V − 1,066 V = −0,025 V
Esercizi riassuntivi e integrativi
1. Calcolare la f.e.m. di una pila formata da un elettrodo standard ad idrogeno
e da un elettrodo di cromo immerso i una soluzione 1,0·10−3M dello ione Cr3+
(E°Cr+3/Cr =-0,742 V). Scrivere, inoltre, la reazione complessiva e calcolarne la
costante di equilibrio. [R. f.e.m.=0,801 V]
2. Una pila di concentrazione è formata da due semicelle nelle quali gli
elettrodi di platino sono immersi in due soluzioni, una 0,100 M di HCl e
l’altra 0,100 M di CH3COOH (Ka=1,8 10-5). H2 alla pressione di 1 atm è fatto
gorgogliare sui due elettrodi e la temperatura è di 298 K. Calcolare la forza
elettromotrice della pila. [R. f.e.m.=0,111 V]
3. Una pila è formata da un elettrodo a idrogeno (PH2= 1 atm) immerso in una
soluzione di acida e da un elettrodo di rame immerso in una soluzione di
CuSO4 0,100 M. La f.e.m. della pila è 0,400V a 298 K. Calcolare [H+] nella
semicella a idrogeno. [R. [H+]= 3,31·10-2M]
4. Un elettrodo standard a idrogeno è collegato a un elettrodo a idrogeno
(PH2= 1 atm; T=298K) immerso in una soluzione 0,105 M di un acido debole
monoprotico (HA). La f.e.m. della pila è 0,170V. Calcolare Ka dell’acido
debole. [R. Ka= 1,75·10-5 M]
5. Calcolare la f.e.m. della seguente pila a concentrazione:
Ag
Ag
| Ag2SO4 (soluzione satura) | | Ag+(0,100 V) |
sapendo che il prodotto di solubilità di Ag2SO4 è 1,6 10-5 M3. [R=0,029 V]
Esercizi riassuntivi e integrativi
6. A 25°C, la f.e.m. della pila
Pt(+)
Pt (-)
(1 atm) H2 | [HCl]= ? M | | [HA]=0,10 M | (1 atm) H2
vale 0,0677 V. Si calcoli la concentrazione di HCl al catodo. Per l’acido
debole monoprotico (HA) la costante di acidità Ka è pari a 5,10·10-5 (mol/L).
[R. [HCl] =0,096 M]
7. Determinare la costante di equilibrio della reazione
Zn + 2Ag+ = Zn2+ + 2Ag
sapendo che la f.e.m. della pila
Zn(-)
Ag(+)
| [ZnSO4]=5·10-3 M | | [AgNO3]=0,01 M |
è pari a 1,51 V a 25°C.
[R. K=6,3·10+52]
8. Si calcoli la f.e.m., a 25°C, della pila
Cu(-)
Pt(+)
| [Cu2+]=0,1 M | | [Fe3+]=0,1M; [Fe2+]=0,1M |
sapendo che la costante di equilibrio della reazione:
2Fe3+ + Cu = 2Fe2+ + Cu2+
alla temperatura di 25° C, vale 4,86·10+14. [R. f.e.m.=0,464 V]
Esercizi riassuntivi e integrativi
9. Sapendo che la costante di equilibrio dell'acido debole HA vale KA= 5,0 ·1 0-4M,
si calcoli la forza elettromotrice della pila:
Pt
Pt
H2(0,5 atm)| [KCl]=0,10 M | | [HA]=0,10 M |H2(1 atm)
Si calcoli anche la forza elettromotrice della pila quando, nella soluzione del
semielemento di destra (di volume pari a 1 litro), si aggiungono 5,0 ·1 0-2mol di
KOH solido.
[Prima dell'aggiunta: ∆E=0,277V; dopo dell'aggiunta: ∆E=0,209V]
10. La costante di equilibrio della reazione:
Hg2+ + 2Fe+2 = Hg + 2Fe+3
vale K=5,66 M-1 a 25°C. Si determini la f.e.m della pila:
Pt
Hg
| [Fe+2]=1·10-2 M; [Fe+3]=5·10-3 M | | [Hg+2]=0,1 M |
[R. f.e.m.=0,01049 V]
Esercizi riassuntivi e integrativi
11. A 25,0°C, la forza elettromotrice della seguente pila :
Pt(+)
Pt(-)
H2 (1 atm) | [HCl]= x M | | [HA] =0,01 M | H2 (1 atm)
vale ΔE=67,7 mV. Si calcoli la concentrazione di HCl nella soluzione del
semielemento positivo della pila. Per HA Ka = 5,10·10-4M. [ R.: [HCl]=0,096M]
12. Sapendo che i potenziali standard delle coppie: Fe3+/Fe2+ e Cr2072-,H+/Cr3+
valgono, rispettivamente, +0,77 V e + 1,33V, si stabilisca per quale valore del
pH è nulla la forza elettromotrice della pila:
Pt
Pt
| [Fe3+]=0,05 M, [Fe2+]=0,10 M | | [Cr2O72-] =0,02 M,[Cr3+]=0,10M, [H+]=?M |
[ R.: pH=4,21]
13. Sapendo che i potenziali standard delle coppie Au3+/Au+ e Mn04-,H+/Mn2+
valgono, rispettivamente, +1,29V e +1,51V, si stabilisca per quale valore del pH è
nulla, alla temperatura di 25,0°C, la forza elettromotrice della pila:
Pt
Pt
| [Au3+] = 0,05M, [Au+] = 0,10 M | | [Mn04-] = 0,02M, [Mn2+] = 0,1 M, [H+]=?M |
[R.: pH = 2,33]
Esercizi riassuntivi e integrativi
14. La forza elettromotrice della seguente pila:
Pt(-)
Cu(+)
(Ptot=1,0 atm) (H2 + Ar) | [HCl]=0,001 M | | [CuSO4]=0,01 M |
vale M = 0,454 V a 25,0°C. Sapendo che: E°Cu2+/Cu=0,340V, si calcoli la frazione
molare di Ar nella miscela gassosa che gorgoglia sull'elettrodo di platino.
[χ
χAr=0,279]
15. Il potenziale di un elettrodo di idrogeno (PH2=1 atm) immerso in una soluzione
0,74 M di cianuro di potassio (KCN) vale E=-0,68 V, a 25°C. Determinare il valore
della costante di dissociazione dell'acido cianidrico (HCN), alla stessa temperatura.
[Ka=7,20·10-10M]
16. La fem della pila, a 25°C,
Pt(-)
Ag(+)
(1,0 atm) H2 | [NaCl]=0,10 M | | [AgNO3]=0,30 M |
vale 1,183V. Se si aggiungono, nel semielemento di destra (V=1000 mL), 0,10 mol di
K3PO4, si ha la precipitazione di Ag3PO4 e la fem nella nuova situazione (polarità
degli elettrodi invariate) diventa pari a 0,958V. Si calcoli il valore del prodotto di
solubilità di Ag3PO4. [KS=1,646·10-18 M4]
Esercizi riassuntivi e integrativi
17. Sia data la pila, a 25°C:
Ag
Ag
| Ag2CrO4 soluzione satura | | [AgNO3]=0,10 M |
Nella soluzione del semielemento di destra (V = 1000 mL) si aggiungono 0,1 mol di
NaCl solido. Sapendo che i prodotti di solubilità di Ag2CrO4 e di AgCl valgono,
rispettivamente, 1,9·10-12M3 e 1,032·10-10 M2,calcolare la fem della pila prima e
dopo l’aggiunta di NaCl. [∆Eprima=0,166 V; ∆Edopo=0,070 V ]
18. A 25°C, la fem della pila:
Pt
Pt
(1,0 atm) H2 | [NaNO3]=0,10 M | | [NaNO2]=0,01 M | H2 (1,0 atm)
vale 0,040 V. Si determini il valore della costante di dissociazione acida (Ka) di
HNO2. [Ka=4,43·10-4 M]
Da gennaio 2012 a settembre 2012
potrete trovarvi ogni venerdì mattina
(salvo esami o impegni istituzionali)
presso la stanza 125 (primo piano).
Per comunicazioni telematiche la mia
e-mail è [email protected]
(specificare sempre l’oggetto:
STUDENTE TARANTO).
Solo per comunicazioni urgenti
telefonare al numero 080-5963601
oppure 080-5963600 chiedendo
del Dott. Giuseppe Romanazzi.
Gli appelli degli esami di profitto per l’anno solare 2012
relativi all’insegnamento di Chimica (6 cfu) per il Corso di
Laurea (interfacoltà) in Ingegneria per l’Ambiente e il
Territorio (DM 270/2004) seguiranno il seguente calendario:
Le date potranno subire variazioni (ovviamente piccole posticipazioni)
“In bocca al lupo per
la prova di esame e
per il prosieguo dei
vostri studi”
THE END