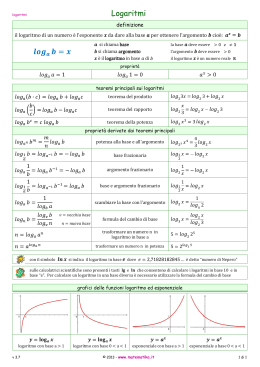
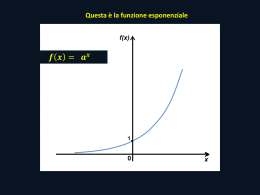
Classificazione di funzione
Luca Cuniberti
Classe: IV E
Anno Scolastico 2007/2008
IPSIA “A. CASTIGLIANO” ASTI
ORGANIGRAMMA DELLE
FUNZIONI
FUNZIONE
Dati due insiemi non vuoti A e B si dice FUNZIONE
da A a B una relazione tra i due insiemi che AD
OGNI x ∈ A fa corrispondere UNO E UN SOLO y
∈ B.
FUNZIONI ALGEBRICHE
Dati due insiemi non vuoti A e B si dice FUNZIONE
da A a B una relazione tra i due insiemi che AD
OGNI x ∈ A fa corrispondere UNO E UN SOLO y
∈ B.
La sua espressione matematica ha una
rappresentazione di tipo algebrico.
FUNZIONI ALGEBRICHE
RAZIONALI
La sua espressione matematica ha una rappresentazione di tipo
algebrico con polinomi di vario grado. Le funzioni possono essere
INTERE o FRATTE
Esempi:
yx
INTERA
2
1
y
x 1
FRATTA
FUNZIONI ALGEBRICHE
IRRAZIONALI
 La sua espressione matematica ha una rappresentazione di
tipo algebrico con radicali che contengono l’incognita. Le
funzioni possono essere INTERE o FRATTE.
 Esempi:
x  2x  3
2
INTERA
x 1
2
x2
FRATTA
FUNZIONI TRASCENDENTI
 Le funzioni trascendenti sono tutte quelle
funzioni che NON sono algebriche. Le
funzioni trascendenti si dividono in:
 - ESPONENZIALI
 - LOGARITMICHE
 - GONIOMETRICHE
FUNZIONI ESPONENZIALI
 Quando una funzione è espressa mediante un numero
elevato all’esponente la funzione è detta funzione
esponenziale , ha come base un numero e come
esponente la variabile indipendente espressa da un
numero reale (R).
ESEMPIO DI FUNZIONE
ESPONENZIALE
3
# : f ( x) : y   
2
x
FUNZIONI LOGARITMICHE
 La funzione logaritmo in base a è la funzione inversa
rispetto alla funzione esponenziale in base a.
 Si dice, cioè, logaritmo in base a di un numero x
l'esponente da dare ad a per ottenere x (x viene chiamato
argomento del logaritmo). In altre parole, se
– X=ay
 segue che:
– Y = loga x
 (si legge: y è il logaritmo in base a di x).
 Per esempio, log3 81 = 4 perché 34 = 81.
ESEMPIO DI FUNZIONE
LOGARITMICA
FUNZIONI GONIOMETRICHE
 Le funzioni nelle quali la variabile indipendente è un angolo
(o un arco) vengono dette goniometriche o circolari.
Per definire le funzioni goniometriche elementari si
consideri fisso il lato di origine degli angoli (identificato, nel
caso del riferimento cartesiano ortogonale xOy, col
semiasse positivo delle ascisse) e variabile il secondo.
Si consideri ora nella seguente figura l'angolo orientato b il
cui primo lato coincide appunto col semiasse positivo delle
ascisse e il secondo è la semiretta r
Sia P un generico punto della semiretta
r,siano xp e yp le sue coordinate e sia
OP la distanza assoluta di P dall'origine
O. I quattro rapporti:
Yp/Op; Xp/Op; Xp/Yp; Yp/Xp
ESEMPIO DI FUNZIONE
GONIOMETRICA