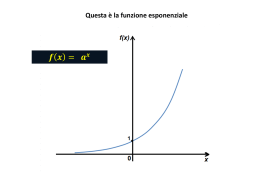
Questa è la funzione esponenziale
Questa è la funzione esponenziale
Consideriamo
f(x) =
a=2
2x
Se diamo alla x il valore X = 1, otteniamo per la funzione
Mentre se diamo alla x il valore X = 10, otteniamo per la funzione
Aumentando il valore della x di 10 volte il valore della funzione
aumenta di più di 1000 volte
Questo fatto può essere molto scomodo quando si
devono eseguire calcoli
e poiché le funzioni esponenziali, in modo più o meno
complicato, sono usatissime in vari campi, questo capita
molto spesso
Per aggirare l’ostacolo dovuto alla scomodità del calcolo si ricorre
ad un «trucco»:
Poiché, in una funzione esponenziale, la base è sempre la stessa, è
possibile utilizzare nei calcoli i valori degli esponenti e solo
successivamente il valore della funzione
f(x) = ax
CONCENTRIAMOCI SULL’ESPONENTE X
X è il valore da dare all’esponente della base a
per ottenere il valore della funzione
Esempio 1:
6 è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
X è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
Esempio 2:
4 è il valore dell’esponente della base a = 3 che ci
permette di ottenere il valore della funzione
X è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
Esempio 3:
- 4 è il valore dell’esponente della base a = 5 che ci
permette di ottenere il valore della funzione
X è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
Invertiamo i ruoli tra l’esponente e la funzione esponenziale
in modo da ottenere il valore dell’esponente conoscendo la
funzione
X è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
Invertiamo i ruoli tra l’esponente e la funzione esponenziale
in modo da ottenere il valore dell’esponente conoscendo la
funzione
X , il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione, si chiama
LOGARITMO IN BASE a DI x
x = loga(ax)
X , il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione, si chiama
LOGARITMO IN BASE a DI x
x = loga(ax)
Invertiamo i ruoli tra l’esponente e la funzione esponenziale in modo
da ottenere il valore dell’esponente conoscendo la funzione
E' una funzione biunivoca, perché
ad ogni valore di f(x)
corrisponde un solo valore di x
Quindi è una funzione invertibile, cioè
esiste una funzione tale che
x = f -1 (y)
da y = ax si passa a x = f-1 (y)
Funzione inversa
x = f-1 (y)
Per ottenere la funzione inversa è
sufficiente che l’asse delle x con tutti i
valori della x (ESPONENTI) prenda il
posto dell’asse delle y (VALORI DELLA
FUNZIONE) e viceversa
x
1
f(x)
1
x
f(x)
f(x) = logax
a>1
1
x
f(x) = ax
0<a<1
f1(x) = loga x
f2(x) = logb x
f1(x) = loga x
f2(x) = logb x
0<a<1
a>1
Le due funzioni
f(x) = loga x
e
f(x) = a x
Sono simettriche
rispetto alla bisettrice
del I e del II quadrante
f(x) = loga x
X è il valore dell’esponente della base a che ci permette di
ottenere il valore della funzione
PROPRIETA’ DEI LOGARITMI
IL LOGARITMO DI UN PRODOTTO E’ UGUALE ALLA
SOMMA DEI LOGARITMI
PROPRIETA’
IL LOGARITMO DI UN RAPPORTO E’ UGUALE ALLA
DIFFERENZA DEI LOGARITMI
PROPRIETA’
IL LOGARITMO DI UNA ESPONENZIALE E’ UGUALE AL
PRODOTTO DELL’ESPONENTE PER IL LOGARITMO DELLA
BASE