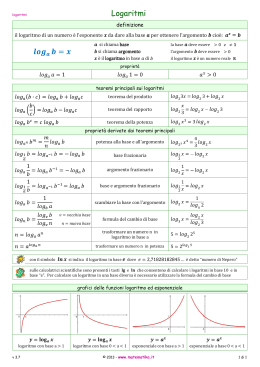
ITCS E. Bona
1
Biella
Definizione di logaritmo
Per ogni numero reale positivo a 6= 1, per ogni numero reale positivo b, il
logaritmo in base a di b, indicato con loga b, è l’esponente a cui elevare la
base a per ottenere b:
c := loga b ⇐⇒ ac = b,
∀a, b ∈ R, b > 0, a > 0 e a 6= 1.
Ad esempio, il logaritmo in base 2 di 1024, che si indica con log2 1024, è
uguale a 10 perché 210 = 1024.
Con i logaritmi risolviamo le equazioni esponenziali. Ad esempio, la
soluzione dell’equazione esponenziale
3x = 11
è il valore dell’esponente x a cui elevare 3 per ottenere 11, per la definizione
di logaritmo:
x = log3 11 = 2, 1826 . . .
Osserva che, come in questo caso, il logaritmo può assumere valori irrazionali.
Link a un video con la definizione di logaritmo.
1
ITCS E. Bona
2
Biella
Proprietà dei logaritmi
Dalla definizione si ricavano immediatamente le seguenti proprietà: ∀a, k ∈
R, a > 0 e a 6= 1,
• loga a = 1, perché a1 = a;
• loga 1 = 0, perché a0 = 1;
• loga (ac ) = c, perché con loga (ac ) stiamo chiedendo qual è l’esponente
a cui elevare a per ottenere ac .... un po’ come chiedere di che colore è
il cavallo bianco di Napoleone.
Le seguenti proprietà non sono immediate e non le dimostriamo ma ci limitiamo ad osservare, con degli esempi, che corrispondono alle proprietà
delle potenze: sono le proprietà delle potenze scritte dal punto di vista degli
esponenti.
Logaritmo di un prodotto ∀a, b1 , b2 ∈ R, con a > 0 e a 6= 1, b1 > 0 e
b2 > 0,
loga (b1 · b2 ) = loga b1 + loga b2
Esempio: log5 (25 · 625) = log5 25 + log5 625. Infatti, calcoliamo separatamente il valore dei due membri dell’uguaglianza:
• log5 (25 · 625) = log5 (52 · 54 ) = log5 (52+4 ) = 6 perché log5 56 = 6
• log5 25 + log5 625 = log5 52 + log5 54 = 2 + 4 = 6
La chiave di questo esempio sta nell’uguaglianza 52 · 54 = 52+4 . Questa
proprietà dei logaritmi è equivalente alla nota proprietà delle potenze
an · am = an+m .
Logaritmo di un quoziente ∀a, b1 , b2 ∈ R con a > 0 e a 6= 1, b1 > 0 e
b2 > 0,
b1
= loga b1 − loga b2
loga
b2
27
Esempio: log3
= log3 27 − log3 81. Infatti, calcoliamo separata81
mente il valore dei due membri dell’uguaglianza:
27
1
1
• log3
= log3
= −1 perché 3−1 =
81
3
3
• log3 27 − log3 81 = log3 33 − log3 34 = 3 − 4 = −1
2
ITCS E. Bona
Biella
Logaritmo di una potenza ∀a, b, k ∈ R con b > 0, a > 0 e a 6= 1,
loga bk = k · loga b
Esempio: log2 (163 ) = 3 · log2 16 infatti
h i
3
= log2 23·4 = 3 · 4 = 3 · log2 24
log2 163 = log2 24
Formula del cambiamento di base ∀a, b, c ∈ R, con a > 0 e a 6= 1, b > 0,
c > 0 e c 6= 1,
logc b
loga b =
logc a
Con le calcolatrici è possibile calcolare il soltanto il logaritmo con base
10 (logaritmo decimale indicato con log) e con base il numero di Nepero
e (logaritmo naturale indicato con ln). Il valore di un logaritmo in
una qualsiasi altra base si calcola trasformandolo in base 10 o base e:
Esempi:
• log3 7 =
log 7
' 1.77
log 3
2
ln
2
• log5 = 3 ' −0.252
3
ln 5
Link a un video sulle proprietà dei logaritmi (I parte).
Link a un video sulle proprietà dei logaritmi (II parte).
3