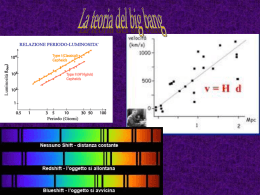
Corso di Astrofisica I
Lezione n. 1:
Cosmologia
La legge di Hubble
Le galassie hanno spettri le cui righe sono
sistematicamente spostate verso il Rosso. Questo
fatto e’ interpretato come effetto Doppler. Un
maggior spostamento verso il rosso indicherebbe
una maggire velocita’ di allontanamento. Hubble
scopri’ che esiste una relazione lineare tra tale
velocita’ e la distanza delle galassie.
Quindi, l’Universo si sta espandendo
Oggi
mB e’ la magnitudine assoluta nella banda B
che cresce con la distanza, mentre z e’ il
redshift che e’ proporzionale alla velocita’ di
espansione.
L’equazione di Friedman-Lamaitre
l  a ( t )l
dl
 al
dt
0
0
2
1  dl  GM 1
GM
E   
 a l 
2  dt 
l
2
al
2
2
0
0
2E
GM
 a  2
l
al
2
2
3
0
0
8G
a 
 k
3a
2
0
4
M
l
3
3
0
Universi Possibili
La costante k nella cosmologia
Newtoniana rappresenta l’energia
totale (invariante). Nella cosmologia
relativistica e’ legata alla curvatura
dello spazio.
8G 

a 1 
  k
3aa 

2
0
2


a
0
3
8G 8G 



a
3
H

3
a
3H
 
 10 g  cm
8G
2
2
C
2
2
 29
C
3
Universi Possibili:
E 0

 1


c
k=0  Universo piatto
8G
aa 
3
1
2
a t
3

0

2
  (6G )
a  da  cos t  dt
1
2
a  t
2
3
1
3
0
1
a 3 t
3
H 
 t
a 2t
2
3
2
2

2
t
3H
Universi possibili:
a
E0

 1

k>0  Universo chiuso
8G
a 
k
3a
8G
a 
3k
2
0
0
MAX
a

c
Universi possibili:
E0

 1


c
k<0  Universo aperto
8G
a 
 ( k )
3a
t  
a   k
2
0
2
( finito
a
a (t )  t
a (t )  t
2
3
(t   0)
(t   )
positivo)
Dominio della radiazione
Per a0 (t0) la densita’ di energia a
riposo della materia (E=c2) diventa
molto grande. La pressione associata
non puo’ piu’ essere trascurata nelle
equazioni dinamiche.
1
 c 
a (t )
2
M
3
Anche la densita’ di energia della
radiazione deve essere tenuta in
conto. In questo caso, pero’, bisogna
considerare l’effetto del redshift, che
induce un ulteriore 1/a.
1
c 
a (t )
2
R
4
L’Universo primordiale era, quindi,
dominato dalla radiazione
In questo caso: a%t1/2 invece che t2/3.
Essendo:
E   c  T
2
R
4
R
1
4
T    1 / a (t )
R
R
10
10
T 
t (sec)
R
t=1 sec KT=1 MeV
g  e- e+
Le componenti dominanti nei
primi secondi sono state:
Radiazione + coppie + neutrini