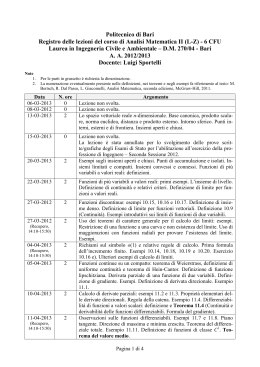
probabilità
• Probabilità totale
• Probabilità delle
prove bernoulliane
• Teorema di Bayes
Probabilità totale o completa
La formula della probabilità totale o completa permette di
calcolare la probabilità di un evento A somma logica di n
elementi incompatibili a due a due, eventi che sono ognuno
prodotto logico di due eventi.
Se {H1, …, Hn}è partizione di U:
P(A) = P(H1)·P(A/H1)+P(H2)·P(A/H2)+…+P(Hn)·P(A/Hn) =
i=n
= ∑P(Hi)·P(A/Hi)
i=1
esempio
esempio
Probabilità delle prove bernoulliane
Per ogni prova sia p la probabilità che la prova dia esito
positivo e sia q=1-p la probabilità contraria.
Vogliamo calcolare la probabilità che su n prove
indipendenti, k e solo k abbiano successo.
Il numero degli eventi formati da k successi e da n-k
fallimenti è dato da tutte le combinazioni delle n prove a k a
k e quindi è ( nk ).
La probabilità che, su n prove bernoulliane, k e solo k
abbiano successo è data da:
Pk=( nk )pk·qn-k
0kn
esempio
Teorema di Bayes
Dal teorema si rileva che le probabilità «a posteriori» P(Hi/A) delle
cause, sono proporzionali alle corrispondenti probabilità «a priori»
P(Hi) corrette con il fattore P(A/Hi).
In soldoni, se è alta la probabilità che l’evento A sia effetto della
causa Hi, il fatto che l’evento A si sia verificato aumenta la
probabilità, anche se non dà la certezza, che a produrlo sia proprio
la causa Hi. Viceversa, se è bassa la probabilità che l’evento A sia
effetto della causa H1, il fatto che l’evento A si sia verificato
diminuisce la probabilità che a produrre A sia stata proprio la
causa Hi.
P(Hi)·P(A/Hi)
P(Hi/A) = –––––––––––––––
i=n
∑ P(Hi)·P(A/Hi)
i=1
esempio