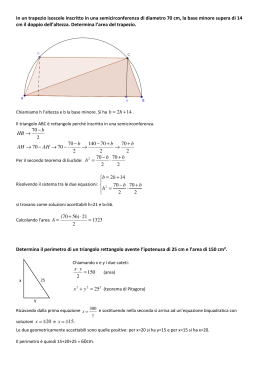
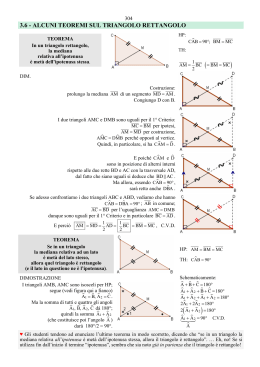
II Teorema di Euclide
In un triangolo rettangolo il quadrato costruito sull’altezza relativa
all’ipotenusa è equivalente al rettangolo avente come lati le proiezioni
dei cateti sull’ipotenusa.
Dimostrazione:
Si costruiscano i quadrati di lati
rispettivamente AB e AH e si effettui la
costruzione del rettangolo di lati BC e BH,
così come fatta nella dimostrazione del
primo teorema di Euclide. Da quest’ultimo
rettangolo si tolga il quadrato di lato BH.
In riferimento alla figura a destra, per il
primo teorema di Euclide si ha:
D
A
Q1
E
Q2
B
Q3
G
Considero il triangolo ABH e per il teorema
di Pitagora si ha che:
F
R
M
Per la proprietà transitiva dell’equivalenza
segue che:
Sottraendo
Erasmo Modica
www.galois.it
H
ad ambo i membri dell’uguaglianza ottenuta, si ha:
L
C