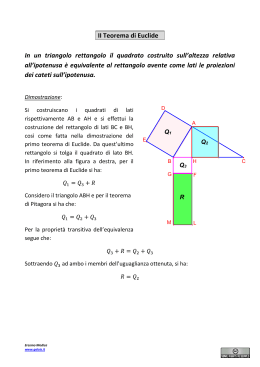
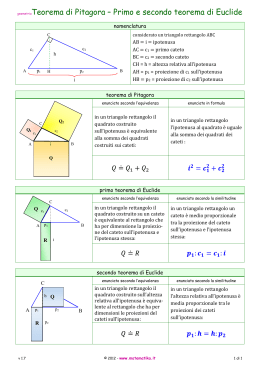
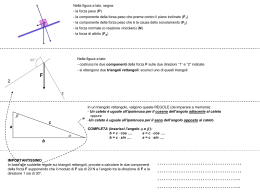
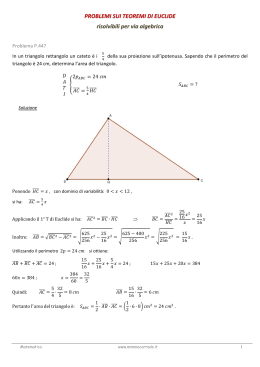
PRIMO TEOREMA DI EUCLIDE
Teorema:
In ogni triangolo rettangolo, ciascun cateto è medio proporzionale tra l’ipotenusa e la
proiezione del cateto sull’ipotenusa.
Dimostrazione grafica:
è una proporzione continua, quindi il prodotto dei medi
è uguale al prodotto degli estremi:
quindi il quadrato costruito sul cateto è EQUIVALENTE (stessa area) al rettangolo
che ha per base l’ipotenusa e per altezza la proiezione del cateto stesso sul’ipotenusa.
Analogamente per l’altro cateto:
SECONDO TEOREMA DI EUCLIDE
In ogni triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra
le proiezioni dei cateti sull’ipotenusa.
Dimostrazione grafica:
il prodotto dei medi è uguale al prodotto degli estremi:
Quindi il quadrato costruito sull’altezza è EQUIVALENTE (stessa area) al
rettangolo che ha per base una proiezione e per altezza l’altra proiezione
sull’ipotenusa.