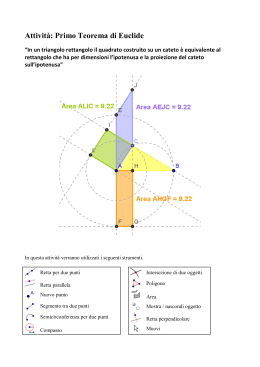
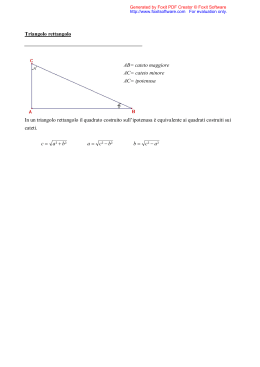
PROBLEMI SUI TEOREMI DI EUCLIDE
risolvibili per via algebrica
Problema P.447
In un triangolo rettangolo un cateto è i
della sua proiezione sull’ipotenusa. Sapendo che il perimetro del
triangolo è 24 cm, determina l’area del triangolo.
2
= 24 = = ?
Soluzione
Ponendo = , con dominio di variabilità: 0 < < 12 ,
si ha:
= Applicando il 1° T di Euclide si ha:
Inoltre:
∙ = .
-
⇒
625 - 25 625 − 400 225 15
= 5
- = 7
.
. - − − =7
=7
=
.
256
16
256
256
16
Utilizzando il perimetro 2
= 24 si ottiene:
+ .
+ = 24 ;
.
60 = 384 ;
Quindi:
25
- 16 - 25
=
.
=
=
16
=
=
384 32
=
60
5
5 32
∙
= 8 4 5
Pertanto l> area del triangolo è:
Matematica
15
25
5
+ + = 24 ;
16
16
4
=
=
.
15 + 25 + 20 = 384
15 32
∙
= 6 16 5
1
1
∙ = B ∙ 6 ∙ 8C - = 24 - .
⋅ .
2
2
www.mimmocorrado.it
1
Problema Z.G323]
In un triangolo rettangolo la proiezione di un cateto sull’ipotenusa è i
del cateto stesso, mentre la
D
proiezione dell’altro cateto sull’ipotenusa ha lunghezza 65 cm. Determina il perimetro del triangolo.
= 65 . = .
D
2
= ?
Soluzione
EFGHGIF . = , con dominio di variabilità: > 0 ,
4
4
= + 65
= H
.
.
9
9
Applicando il I Teorema di Euclide al triangolo ABC si ha:
PQ ℎS:
;
- = .
∙ .
.
81 - = 16 - + 2340 ;
4
4
- = ∙ B + 65C ;
9
9
65 - − 2340 = 0 ;
4
∙ 36 = 16 9
Applicando il Teorema di Pitagora al triangolo ABC si ha:
EHYZSGZF: . = 36 =
.
- =
16 - 260
+
;
81
9
- − 36 = 0 ;
H
∙ U − 36V = 0 ;
= 0 WX
= 36 = U16 + 65V = 81 .
.
= 5
- = 581- − 36- = √6561 − 1296 = √5265 = 9√65 . - − .
EHYZSGZF è:
Matematica
+ = \36 + 81 + 9√65] = \117 + 9√65] .
2
= . + .
www.mimmocorrado.it
2