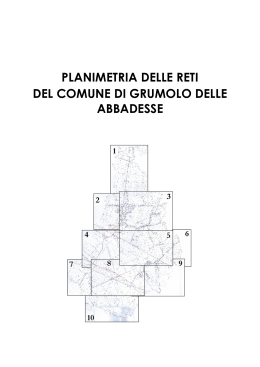
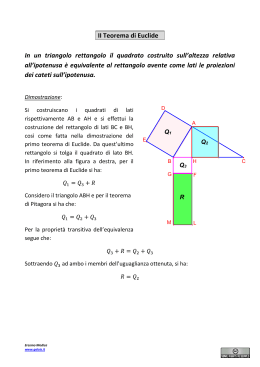
Le scale di riduzione
Le dimensioni di un oggetto, quando sono troppo grandi perché siano riportate sul
foglio da disegno, si riducono in scala.
Scala 1 a 200 (si scrive 1 : 200) rappresenta una divisione. In scala 1: 200, il valore
che riporterai sulla carta sarà il valore reale della lunghezza diviso per 200, in scala
1:50 sarà diviso per 50, in scala 1:1000 sarà diviso per 1000.
Per esempio, partiamo da una misura sul terreno di 8,40 m.
Trasformiamo prima in centimetri, (perché si disegna in centimetri).
8,40 m => 840 cm e riduciamo in scala 1: 200 => 840 : 200 = 4,2 cm
Abbiamo ottenuto che una lunghezza di 8,40 m, corrisponde a un segmento di 4,2
cm sulla carta, in un disegno in scala 1:200.
Se poi dovremo passare dal valore misurato su carta al valore reale, faremo
l'operazione inversa, cioè moltiplicheremo la lunghezza del segmento misurato sul
disegno per 200, o per 50, o per 1000, per ottenere la lunghezza nella realtà.
Andiamo ora a vedere le formule generali.
Abbiamo detto che per passare dalla misura reale a quella del disegno si divide la
misura reale per la scala:
𝐿𝐷 =
𝐿𝑅
𝑁
dove LD è la lunghezza sul disegno, LR quella reale e N è il denominatore della scala
(1:N).
Quindi 840 cm : 200 = 4,2 cm (lunghezza sul disegno).
Se conosco la misura reale dell’oggetto e la sua misura sul disegno, posso ricavare la
scala con cui è stato eseguito il disegno dalla formula:
𝑁=
𝐿𝑅
𝐿𝐷
840 cm : 4,2 cm = 200 => la scala è quindi 1:200.
Se si vuole la misura reale, nota la misura del disegno e la scala:
𝐿𝑅 = 𝐿𝐷 𝑥 𝑁
4.2 cm x 200 = 840 cm (lunghezza reale)
Altro esempio: 320 m => scala 1:2000
LD =320 m / 2000 = 0.16 m
LR = 0.16 x 2000 = 320 m
N = 320 m / 0.16 m = 2000
Calcolo dell’area su un disegno
b
h
Facciamo riferimento a un rettangolo, ma il ragionamento vale per tutte le figure.
 In un disegno, eseguito in scala 1:2000, un terreno di forma rettangolare ha
dimensioni h = 4.3 cm e b =7.2 cm. Determinare l'area reale del terreno.
Per determinare l'area di una figura in scala bisogna prima di tutto trovare le
dimensioni reali e poi, in seguito, calcolare l'area.
L’area del rettangolo, com’è noto, si determina con la formula:
A=bxh
Trasformiamo prima i lati in metri:
7.2 cm / 100 = 0.072 m e 4.3 cm / 100 = 0.043 m
Poi troviamo le misure reali (quelle del terreno) moltiplicando i lati per la scala:
0.072 m x 2000 = 144 m e 0.043 m x 2000 = 86 m
Il terreno avrà quindi queste dimensioni:
144 m
86 m
e la sua area varrà : A = 86 m x 144 m =12 384 m2
E’ sbagliato calcolare l’area con le dimensioni del disegno e poi moltiplicare per la
scala:
0.072*0.043*2000=6.192 m2
bisogna invece moltiplicare per la scala al quadrato
2
0.072*0.043*2000 =12 384 m2
Altri esercizi:
 Un terreno rettangolare, disegnato in scala 1:2000, sul disegno misura 12 cm
di base e 5.5 cm di altezza. Calcolare l’area reale del terreno.
12 cm
5,5 cm
1: 2000
12 cm x 2000 = 24000 cm = 240 m
5,5 cm x 2000 = 11000 cm = 110 m
Area rettangolo = 240 m x 110 m = 26 400 m2
 Un rettangolo ha l’area A = 500 000 m2 e la larghezza b = 1000 m .
Determinare l’altezza h del rettangolo e la scala da utilizzare per disegnare il
rettangolo in un foglio formato A4
b
h
A=bxh
=>
h = A/b = 500 000 / 1000 = 500 m
Proviamo, ad esempio, con una scala 1:2000
b=1000 m / 2000 = 0,50 m = 40 cm [eccessiva per il formato A4 (max 29,7 cm)]
h=500 m / 2000 = 0,25 m = 25 cm
[eccessiva per il formato A4 (max 21 cm)]
Proviamo allora con la scala 1:5000
1000 m / 5000 = 0,2 m
=>
20 cm => b
500 m / 5000 = 0,1 m
=>
10 cm => h
Si eseguirà quindi il disegno in scala 1:5000
Invece di procedere a tentativi potevamo calcolare un valore approssimato della
scala da arrotondare poi tra i valori delle scale più utilizzati.
Usiamo la formula:
𝑁=
𝐿𝑅
𝐿𝐷
LR1 = 1000 m
LR2 = 500 m
Per LD prendiamo le dimensioni del foglio (21 cm x 29,7 cm) e troviamo due valori
della scala:
𝑁1 =
1000 𝑚
= 3367
0,297 𝑚
𝑁2 =
500 𝑚
= 2380
0,21 𝑚
e
Ovviamente utilizzeremo una riduzione in scala maggiore di 3367 per verificare le
due condizioni. Arrotondiamo la scala 1: 3367 alla scala più prossima 1: 5000.
Lo studente può poi controllare, per esercizio, che il disegno eseguito in scala 1:2000
non entra nel foglio formato A4
 Dello stesso rettangolo si vuole staccare un triangolo con base B =240 m e
area 10000 m2. Calcolare l’altezza h che avrà il triangolo e rappresentarla sul
disegno.
Area triangolo => A = B x h/ 2 = 240 x h / 2 = 10000 m2
Ricaviamo h dalla formula inversa dell’area:
h = 2 x A /B = 2x10000/240 = 83,33 m =8333 cm
e poi calcoliamo la misura in scala 1:2000:
h = 8333 cm/2000 = 4,16 cm
h
Le scale maggiormente utilizzate sono:
Disegno tecnico e meccanico

Scala 2:1 = Scala ingrandita: serve per ingrandire gli oggetti;

Scala 1:1 = Scala reale: serve per rappresentare gli oggetti in misura naturale

Scala 1:2 = Scala rimpicciolita;

Scala 1:2,5

Scala 1:5

Scala 1:10

Scala 1:20
Disegno architettonico e urbanistico

Scala 1:5 (dettagli di particolari)

Scala 1:10 (dettagli di particolari)

Scala 1:20 (particolari costruttivi e di arredamento)

Scala 1:50 (progetto esecutivo, arredamento)

Scala 1:100 (progetto architettonico)

Scala 1:200 (progetto preliminare, planimetrie catastali di immobili)

Scala 1:500 (Planimetria)
Cartografia



Scala 1:500 (Planimetria catastale, Carta Tecnica Comunale)
Scala 1:1000 (Planimetria catastale, Carta Tecnica Comunale)
Scala 1:2000 (Planimetria catastale, Carta Tecnica Comunale)

Scala 1:5000 (Carta Tecnica Regionale)

Scala 1:10000 (Carta Tecnica Regionale)

Scala 1:25000 (Carta IGM)

Scala 1:50000 (Carta IGM)

Scala 1:100000 (Carta IGM)

Scala 1:200000/250000 (Carta stradale di dettaglio)

Scala 1:500000 (Carta stradale)