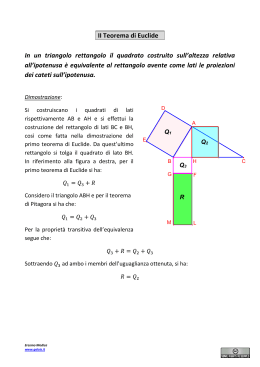
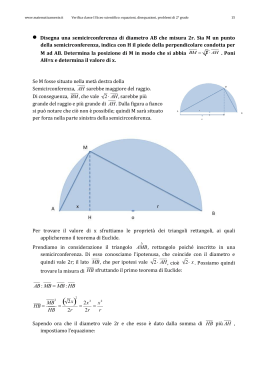
In un trapezio isoscele inscritto in una semicirconferenza di diametro 70 cm, la base minore supera di 14
cm il doppio dell’altezza. Determina l’area del trapezio.
Chiamiamo h l’altezza e b la base minore. Si ha b = 2h + 14 .
Il triangolo ABC è rettangolo perché inscritto in una semicirconferenza.
HB →
70 − b
2
70 − b 140 − 70 + b
70 + b
→
→
2
2
2
70 − b 70 + b
Per il secondo teorema di Euclide: h 2 =
⋅
2
2
AH → 70 − AH → 70 −
b = 2h + 14

Risolvendo il sistema tra le due equazioni:  2 70 − b 70 + b
h = 2 ⋅ 2
si trovano come soluzioni accettabili h=21 e b=56.
Calcolando l’area A =
(70 + 56) ⋅ 21
= 1323
2
Determina il perimetro di un triangolo rettangolo avente l’ipotenusa di 25 cm e l’area di 150 cm².
Chiamando x e y i due cateti:
x
25
x⋅ y
= 150
2
(area)
x 2 + y 2 = 25 2 (teorema di Pitagora)
y
Ricavando dalla prima equazione x = 300 e sostituendo nella seconda si arriva ad un’equazione biquadratica con
y
soluzioni x = ±20 e x = ±15 .
Le due geometricamente accettabili sono quelle positive: per x=20 si ha y=15 e per x=15 si ha x=20.
Il perimetro è quindi 15+20+25 = 60cm.