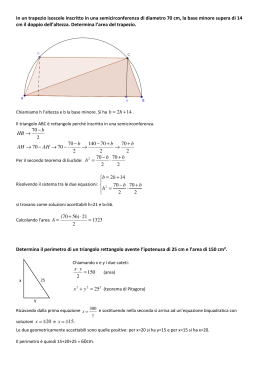
Nome………………………….Cognome……………………….. classe 4D
26 Febbraio 2013
Problema n. 1
E’ data una semicirconferenza di diametro AB = 2r . Inscrivi in essa il triangolo ABC e traccia la bisettrice
dell’angolo CAˆ B che interseca la circonferenza in D e il lato CB in T.
Indicato con 2x l’angolo CAˆ B , determina al variare di x, il rapporto
AT
1
−2
sin 2 x
TD
AT
a) determina per quale valore di x
=1
TD
b) traccia il grafico di y = f (x)
f ( x) =
C
. Verificato che f ( x) =
D
T
x
x
A
B
Problema n. 2
E’ dato un trapezio ABCD rettangolo in  e in D̂ , con base maggiore AB e lato obliquo CB. Sono noti i
seguenti elementi: CD = CB = 3 e ABˆ C =
π
. Sia P un punto del segmento CB, tale che CDˆ P = x . Esprimi
3
la funzione: f ( x) = DP + CP , indicando i limiti entro i quali va considerata. Dopo aver verificato che
3
2 , senza riferimento ai limiti geometrici risolvi la disequazione f ( x) ≥ 0
f ( x) = 3 ⋅
π

sin  − x 
3

sin x +
Nome………………………….Cognome……………………….. classe 4D
26 Febbraio 2013
Problema n. 1
E’ data una semicirconferenza di diametro AB = 2r . Inscrivi in essa il triangolo ABC e traccia la bisettrice
dell’angolo CAˆ B che interseca la circonferenza in D e il lato CB in T.
C
Indicato con 2x l’angolo CAˆ B , determina al variare di x, il rapporto
AT
1
−2
sin 2 x
TD
AT
a) determina per quale valore di x
=1
TD
b) traccia il grafico di y = f (x)
f ( x) =
. Verificato che f ( x) =
D
T
x
x
A
Problema n. 2
E’ dato un trapezio ABCD rettangolo in  e in D̂ , con base maggiore AB e lato obliquo CB. Sono noti i
seguenti elementi: CD = CB = 3 e ABˆ C =
π
. Sia P un punto del segmento CB, tale che CDˆ P = x . Esprimi
3
la funzione: f ( x) = DP + CP , indicando i limiti entro i quali va considerata. Dopo aver verificato che
3
2 , senza riferimento ai limiti geometrici risolvi la disequazione f ( x) ≥ 0
f ( x) = 3 ⋅
π

sin  − x 
3

sin x +
B
Soluzioni
Problema n. 1
E’ data una semicirconferenza di diametro AB = 2r . Inscrivi in essa il triangolo ABC e traccia la
bisettrice dell’angolo CAˆ B che interseca la circonferenza in D e il lato CB in T. Indicato con 2x
AT
1
. Verificato che f ( x) =
−2
l’angolo CAˆ B , determina al variare di x, il rapporto f ( x) =
sin 2 x
TD
AT
a) determina per quale valore di x
=1
TD
b) traccia il grafico di y = f (x)
C
D
T
x
x
A
B
Limitazioni:
π
π
0 < 2 x < quindi 0 < x <
2
4
Osserva che:
per x = 0 il triangolo è degenere e TD = 0 , quindi f(x) non è definita.
π
per x = il triangolo è degenere e AT = 0 , TD = r 2 , quindi f(x)=0
4
π
è quindi opportuno non includere l’estremo x=0, mentre x = può essere compreso oppure no, a
4
scelta.
Dal triangolo rettangolo ACB: AC = 2r cos(2 x)
2r cos(2 x)
AC
=
cos x
cos x
Dal triangolo rettangolo ADB: AD = 2r cos x
2r cos(2 x) 2r (cos 2 x − cos(2 x)) 2r (sin 2 x)
TD = AD − AT = 2r cos x −
=
=
cos x
cos x
cos x
2r cos(2 x)
cos(2 x) 1 − 2 sin 2 x
AT
1
f ( x) =
= cos x2
=
=
=
−2
2
2
2r sin x
sin x
sin x
sin 2 x
TD
cos x
1
1
− 2 =1 ⇒
= 3 C.E. sin x ≠ 0 x ≠ kπ
a)
2
sin x
sin 2 x
Dal triangolo rettangolo ACT: AT =
3
, tenendo conto delle limitazioni geometriche, l’unica
3
3
soluzione accettabile è x = arcsin
≈ 35°
3
⇒ sin 2 x =
1
3
⇒ sin x = ±
b) Il grafico si può ottenere da:
1
1
e infine traslazione in basso di 2 y =
−2
2
sin x
sin 2 x
1 − cos(2 x)
1
1
= − cos(2 x) +
Per tracciare y = sin 2 x bisogna abbassare di grado y =
2
2
2
y = sin 2 x ,
y=
reciproca
y
1
x
−5π/4
−π
−3π/4
−π/2
−π/4
π/4
π/2
3π/4
π
5π/4
−1
Quindi il grafico di f ( x) =
1
π
− 2 con 0 < x < è:
2
4
sin x
y
2
1
x
−π/4
π/4
−1
π/2
3π/4
π
Problema n. 2
E’ dato un trapezio ABCD rettangolo in  e in D̂ , con base maggiore AB e lato obliquo CB. Sono noti i
seguenti elementi: CD = CB = 3 e ABˆ C =
π
. Sia P un punto del segmento CB, tale che CDˆ P = x . Esprimi
3
la funzione: f ( x) = DP + CP , indicando i limiti entro i quali va considerata. Dopo aver verificato che
3
2 , senza riferimento ai limiti geometrici risolvi la disequazione f ( x) ≥ 0
f ( x) = 3 ⋅
π

sin  − x 
3

sin x +
D
3
x
C
120°
3
60°-x
P
60°
B
A
Osservazione: DCˆ B =
Limitazioni: 0 ≤ x ≤
π
6
2π
π
poiché supplementare di ABˆ C =
3
3
quando P coincide con C x = 0
quando P coincide con B x =
π
6
Dal teorema di seni sul triangolo DCP:
3
3⋅
DP
DC
2
⇒ DP =
=
2π
π

π

sin
sin  − x 
sin  − x 
3
3

3

CP
DC
3 sin x
=
⇒ CP =
sin x
π

π

sin − x 
sin  − x 
3

3

3
2
f ( x) = DP + CP = 3 ⋅
π

sin  − x 
3

3
sin x +
2 ≥ 0 si risolve studiando numeratore e denominatore:
La disequazione: 3/ ⋅
π

sin  − x 
3

sin x +
3
2
π
2π
1
π

sin  − x  > 0 ⇒ 2kπ < − x < π + 2kπ ⇒ −
+ 2kπ < x < π + 2kπ
3
3
3
3

sin x ≥ −
La soluzione è quindi: −
π
π
+ 2kπ ≤ x < + 2kπ
3
3
+
-