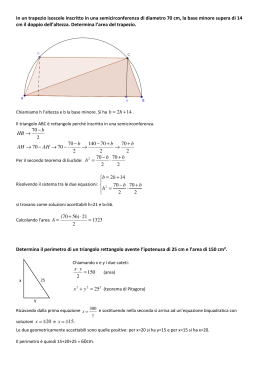
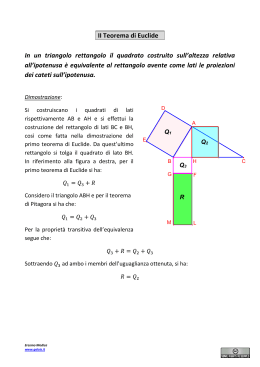
Risoluzione algebrica dei problemi geometrici
La risoluzione algebrica di un problema geometrico avviene in generale secondo i
seguenti passi:
1° passo: Leggere attentamente il testo, cercando di capire bene come rappresentarlo
attraverso una costruzione geometrica e scrivere i dati del problema.
2° passo: Accertarsi di conoscere tutte le proprietà delle figure geometriche
coinvolte (se, ad esempio, il problema riguarda un parallelogramma, occorre conoscere
tutte le sue proprietà) e tutte le espressioni metriche dei teoremi fondamentali.
3° passo: Tracciare una figura seguendo le indicazioni del testo del problema,
segnando sulla figura stessa tutti gli elementi che per ipotesi sono congruenti e
scrivendo le misure note accanto agli elementi cui si riferiscono (ad esempio la misura
di un lato o di un angolo). La figura deve essere generica, per evitare errori nella
risoluzione (se, ad esempio, il problema riguarda un triangolo qualsiasi, occorre evitare
di rappresentare un triangolo isoscele).
4° passo: Scegliere un’incognita (o più incognite) e indicarla sulla figura.
5° passo: Tradurre l’enunciato del problema nel linguaggio algebrico, scrivendo
un’equazione (o un sistema di equazioni) che esprimano una relazione (o più relazioni)
fra i dati del problema e l’incognita (o le incognite).
6° passo: Risolvere l’equazione (o il sistema di equazioni).
7° passo:Discutere il problema per stabilire se le soluzioni trovate sono accettabili (ad
esempio, se l’incognita è un angolo di un triangolo qualunque, la sua misura deve essere
minore di 180°).
•
Nei problemi più semplici l’equazione risolvente è già espressa in forma
algebrica (ad esempio trovare il punto P, in modo che AP+AC+CB=2a). Per
risolvere questo tipo di problemi si devono determinare, in funzione
dell’incognita scelta, tutti gli elementi presenti nell’equazione risolvente che non
sono già noti.
Per esprimere un elemento in funzione dell’incognita si deve individuare la
relazione che intercorre tra l’incognita e l’elemento. Tale relazione può essere
algebrica (ad esempio, se l’incognita è AC=x e AB è uguale al triplo di AC
aumentato di 2 → AB=3AC+2=3x+2) o può essere geometrica (ad esempio, se
l’incognita è AB=x e AC=2, inoltre, il triangolo ABC è rettangolo in A, si può
applicare il teorema di Pitagora e dedurre che BC2=AB2+AC2 =x2+4).
Esempio
Dato il quadrato ABCD, prolungare la diagonale AC dalla parte di A di un segmento
AP=a. Determinare il lato del quadrato in modo che sia verificata la relazione
PC2+PB2+PD2= 51a2.
Risoluzione
1°- 4° passo:
PC2+PB2+PD2= 51a2
AP=a
AB=x
(equazione risolvente)
5° passo: Per risolvere il problema si devono determinare PC, PB e PD in funzione di x.
PC=PA+AC=a+ 2 x (ricordando che la diagonale di un quadrato è uguale al lato
per 2 );
Per determinare PB e PD, si può tracciare la diagonale DB. In tal modo, detto O il
punto di incontro delle diagonali e ricordando che le diagonali di un quadrato sono
uguali e si dimezzano scambievolmente, si ha
che:
DO=OB=AO=OC=x
2
.
2
I triangoli POD e POB sono uguali e rettangoli,
dunque applicando il teorema di Pitagora si ha:
PB2=PD2=OP2+OD2=(a+x
2 2
2 2
) +( x
)
2
2
Sostituendo le espressioni di PC, PB e PD
nell’equazione risolvente si ha:
PC2+PB2+PD2= 51a2
(a+ 2 x)2+2(a+x
2 2
2 2
) +2(x
) =51a2
2
2
6° passo:
(a+ 2 x)2+2(a+x
2 2
2 2
) +2(x
) =51a2 ⇒ a2+2x2+2 2 ax+2a2+x2+2 2 ax+x2=51a2 ⇒
2
2
4x2+4 2 ax-48a2=0 ⇒ x2+ 2 ax-12a2=0 ⇒ x=
− 2 ± 50 − 2 ± 5 2
a=
a ⇒
2
2
x= −3 2 a e x= 2 2 a
7° passo:
La soluzione x= −3 2 non è accettabile, perché la misura di un segmento non può
essere negativa. Dunque il problema ammette come unica soluzione AB= 2 2 a.
•
Nei problemi più complessi l’equazione risolvente è da determinare. Per
individuare l’equazione risolvente è sufficiente individuare una relazione tra gli
elementi coinvolti nel problema, dopo averli espressi in funzione dell’incognita
(ad esempio, il triangolo ABC è rettangolo in A, inoltre AC=4x, BC=3x e
AB=2x+1. Per il teorema di Pitagora si ha (5x+1)2= (4x)2+(3x)2, che rappresenta
l’equazione risolvente). Oppure si può cercare di esprimere la stessa quantità in
due modi diversi, in funzione dell’incognita (ad esempio, applicando il teorema di
Pitagora al triangolo ABC si ottiene che AC=4x+1, invece applicando il primo
teorema di Euclide si ottiene AC=6x-3, dunque l’equazione risolvente è
4x+1=6x-3).
Esempio
Un trapezio isoscele ABCD, di cui AB è la base maggiore, è circoscrivibile a un cerchio.
Il trapezio ABCD è inscritto in una semicirconferenza di diametro AB=2r.
Determinare la base minore CD =2x, il lato BC e il raggio del cerchio inscritto nel
trapezio.
Risoluzione
1°- 4° passo:
AB=2r (per simmetria AH=HB=r)
CD =2x (per simmetria DL=LC=x)
BC=?
OH=?
5° passo: Per risolvere il problema innanzitutto si devono determinare BC e OH in
funzione di x.
Ricordando che i segmenti di tangente
condotti da un punto esterno a una
circonferenza sono congruenti si ha che:
AH=AN=r=KB=BM
ND=DL=x=LC=CM
Pertanto:
BC=BM+CM=r+x
Osservando la figura, è evidente che CK=LH e OH=
1
LH.
2
Poiché il triangolo CKB è rettangolo in K, per il teorema di Pitagora si ha:
CK2=CB2-KB2
Dal momento che:
KB=HB-HK=r-x (perché HK=LC=x)
si ha che:
CK2=CB2-KB2= (r+x)2-(r-x)2=4rx ⇒ CK=2 rx ⇒ OH= rx
A questo punto tutti gli elementi della figura sono stati espressi in funzione di x,
quindi occorre determinare l’equazione risolvente.
Tracciata la diagonale AC, si ha che il triangolo ACB è rettangolo, in quanto inscritto
in una semicirconferenza. Di esso sono noti, in funzione di x, il cateto CB, l’ipotenusa
AB e l’altezza CK.
A tale triangolo si possono dunque applicare il primo e il secondo teorema di Euclide.
Se si sceglie di applicare il primo teorema di Euclide si ha:
CB2=KB ⋅ AB ⇒ CB2=(r+x)2r
Ma CB=BM+CM=r+x, dunque CB2=(r+x)2
Eguagliando le due espressioni di CB2 si ha:
(r+x)2=(r-x)2r ⇒ x2+4rx-r2=0
6° passo:
x2+4rx-r2=0 ⇒ x=-2r ± 5 r
Se si sceglie di applicare il secondo teorema di Euclide si ha:
CK2=KB ⋅ AK
Sostituendo a CK, KB e AK le loro espressioni in funzione di x si ha:
4rx=(r-x)(r+x) ⇒ x2+4rx-r2=0 ⇒ x=-2r ± 5 r
Ovviamente le soluzioni trovate con i due teoremi sono uguali!
7° passo:
La soluzione x=-2r- 5 r non è accettabile, perché la misura di un segmento non può
essere negativa. Dunque x=(-2+ 5 )r e il problema ammette come unica soluzione:
CD=2x=2(-2+ 5 )r, BC=(-1+ 5 )r, OH= r
2
( −2 + 5 ) = r
−2 + 5 .
Problemi
1. Nel triangolo ABC, isoscele sulla base AB, sia AH l’altezza relativa al lato CB.
Determinare CH e HB sapendo che AB e il lato AC sono rispettivamente lunghi 6a e
5a. Determinare, inoltre, sul prolungamento di AH, dalla parte di H, un punto P in
modo che sia verificata la relazione PB² = 2/5 PA².
(CH = 7/5 a; HB = 18/5 a; PH = 6/5 a, 26/5 a)
2. E’ data una semicirconferenza di centro O e diametro AB = 2r. Determinare sul
segmento AB un punto P in modo che, detto C il punto di incontro della
perpendicolare, condotta da P ad AB, con la semicirconferenza, sia verificata la
seguente relazione: 2AC2 + 5CP2 +CB2 = 8r2.
(AP=2r,2/5r)
3. L’area di un triangolo equilatero è di 64 3 cm2. Si prolunghi ogni lato, nello stesso
senso, di un segmento uguale alla quarta parte del lato stesso. Si congiungano gli
estremi di tali segmenti e, dopo aver dimostrato che il triangolo così ottenuto è
ancora equilatero, determinarne perimetro e area.
(2p=12 31 cm; Area=124 3 cm2)
4. Nel trapezio rettangolo ABCD la proiezione HB del lato obliquo CB sulla base
maggiore AB misura a ed è congruente all’altezza. Determinare la misura della base
minore sapendo che è verificata la relazione (CA2+AB2)/CD2=37/8.
(CD=4/3a)
5. Determinare sui lati AB, BC, CD e DA del quadrato ABCD, di area 25a2, i punti M,
N, P, Q in modo che i segmenti AM, BN, CP, DQ siano rispettivamente proporzionali
a 1, 2, 3, 4 e l’area del quadrilatero MNPQ sia 12a2.
(AM=a, 13/12a)
6. Dividere un segmento a in due parti tali che la differenza dei loro quadrati sia d2.
((a2+d2)/2a, (a2-d2)/2a)
7. In un rettangolo ABCD si ha AB=5a e AD=2a. Determinare un punto R su AD e un
punto S su AB in modo che sia DR=
1
1
RS= SB.
2
4
(DR=a(22- 107 )/13)
8. Determinare i cateti AC e BC di un triangolo rettangolo ABC, sapendo che un
cateto differisce dall’altro di
(
)
3 + 1 a e che la differenza tra il doppio del
quadrato dell’ipotenusa e il quadrato della somma dei cateti è equivalente all’area
del triangolo.
(
(
) (
3 + 1 a, 2
)
3 + 1 a)
9. Due corde parallele di una circonferenza misurano rispettivamente 126 cm e 112
cm, e stanno da una stessa parte rispetto al centro. Sapendo che la loro distanza è
di 17 cm calcolare le misure delle loro distanze dal centro e la misura del raggio
della circonferenza.
(33 cm, 16 cm, 65 cm)
10. Calcolare la misura del lato del quadrato inscritto in un triangolo avente la base di
80 cm e l’altezza di 45 cm
(28,8 cm)
11. La base di un triangolo isoscele è i 3/2 dell’altezza e il perimetro misura 64 dm. Dal
centro della circonferenza inscritta nel triangolo si conduca la parallela alla base.
Calcolare l’area dei due poligoni in cui il triangolo dato risulta diviso dalla parallela.
(75 dm2, 117 dm2)
12. Nella circonferenza di centro O e raggio r e’ data la corda AB, lato del quadrato
inscritto. Si conduca per B la retta t perpendicolare ad AB e sia H la proiezione
ortogonale di O su t. Preso un punto P su t nel semipiano, di origine AB, non
contenente il centro O, si determini la lunghezza di PB in modo che il quadrato
costruito sul segmento AP sia equivalente a 8/9 del quadrato costruito sul
segmento PH.
( r 2 ,7r 2 )
13. Sui lati dell’angolo MON di 120° sono dati i segmenti OA = a su OM e OB = 2a su
ON. Si prenda sulla bisettrice dell’angolo MON un punto P e si determini la sua
distanza da O in modo che sia verificata la relazione PO²+PA²=7/4 PB².
(PO = 2a)
14. Sia data una circonferenza di raggio r e sia t una retta a essa tangente. A quale
distanza dalla retta t si deve tracciare una corda PQ della circonferenza, parallela
alla retta t stessa, affinché, dette R ed S le proiezioni ortogonali di P e Q su t, il
rettangolo PQSR abbia perimetro 6r?
(r, 9/5r)
15. Calcola il perimetro e l’area di un triangolo rettangolo ABC, sapendo che la somma
delle proiezioni (BH+CH) dei cateti sull’ipotenusa BC è di 25 cm e che la differenza
delle proiezioni (BH-CH) dei cateti sull’ipotenusa è di 7 cm.
(60 cm, 150 cm2)