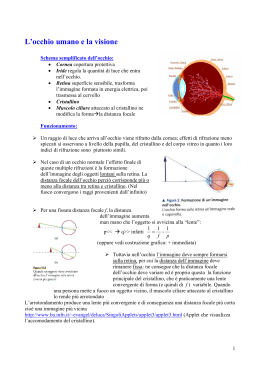
LENTE DI INGRANDIMENTO
¾ Abbiamo visto che la dimensione dell’immagine formata sulla retina aumenta tenendo
l’oggetto sempre più vicino all’occhio .
Consideriamo un oggetto di grandezza h0 che si trovi a distanza N dall’occhio. L’immagine
sottende un angolo θ sulla retina dell’occhio. Se l’angolo è piccolo possiamo approssimarlo con la
tangente dell’angolo stesso (tanθ ≈θ per piccoli angoli) perciò θ ≈h0/N. Se l’oggetto viene spostato
più vicino all’occhio ad una distanza N’, l’angolo sotto cui è vista l’immagine è maggiore, le
dimensioni apparenti dell’oggetto aumentano perché l’immagine copre una maggiore porzione di
retina.
¾ Ricordiamo tuttavia che l’occhio umano non è in grado di mettere bene a fuoco un oggetto
che si trova a distanza inferiore rispetto al punto prossimo. Si usa perciò la lente di
ingrandimento: si tratta di una lente convergente di piccola distanza focale, disposta in modo
tale che l’oggetto da osservare venga a trovarsi fra la lente ed il primo fuoco, producendo
così una immagine virtuale, ingrandita e diritta. (se l’oggetto è posto esattamente nel fuoco,
l’immagine si forma all’infinito). L’occhio utilizza questa immagine ingrandita come
oggetto, l’immagine che si viene a formare sulla retina corrisponde a quella che si
otterrebbe si mettesse sul punto prossimo un ingrandimento dell’oggetto stesso. L’immagine
ottenuta sulla retina inoltre è molto più grande di quella che si otterrebbe osservando
l’oggetto a occhio nudo.
Ingrandimento angolare Se l’altezza dell’oggetto è h0, l’ampiezza angolare sulla retina a occhio
nudo è circa θ = h0/N.
Ora poniamo una lente convessa con distanza focale f<N davanti all’occhio. Se l’oggetto è posto
nel fuoco di questa lente, la sua immagine sarà infinitamente lontana, dove può essere messa a
fuoco con facilità. L’ampiezza angolare dell’immagine è circa θ’ =h0/f da cui risulta un
ingranduimento totale I = θ’/θ = N/f.