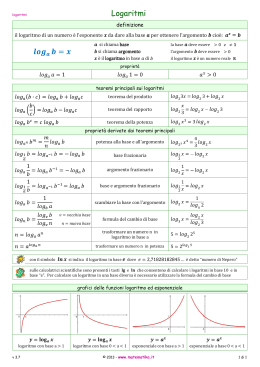
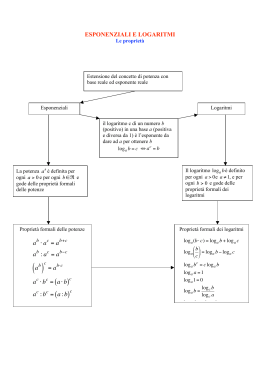
NECESSITÀ DEI LOGARITMI
Nelle equazioni esponenziali che abbiamo risolto sinora era sempre possibile ridursi a equazioni in cui si
aveva la stessa base, l’equazione diventava algebrica semplicemente uguagliando gli esponenti. Ma non
tutte le equazioni sono esponenziali sono riducibili, nei casi non riducibili è necessario introdurre il
concetto di logaritmo.
Un semplice esempio di equazione non riducibile è il seguente: 2 x = 5
Cosa possiamo dire della soluzione di quest’equazione? 5 non è una potenza diretta di 2 , però dato che
2 2 < 5 < 2 3 possiamo dire che sarà 2 2 < 2 x < 2 3 e quindi che 2 < x < 3
Quindi avremo x = 2 ,.... in cui conosciamo almeno la parte intera.
Nella figura qui sotto si vede come individuare graficamente il valore di x
y = 2x
2x = 5
x
Dalla figura si vede che c’è una sola soluzione x all’equazione e che 2 < x < 2 ,5
Con una calcolatrice scientifica è possibile calcolare il valore di x sino a 10 cifre, con la calcolatrice di un
PC si ottiene: x = 2,3219280948873623478703194294894…
Nei calcoli matematici si introduce una nuova operazione: il logaritmo proprio per rappresentare in
modo esatto tale valore.
Si dice quindi che:
IL LOGARITMO IN BASE 2 DI 5 È QUEL NUMERO x TALE CHE 2 x = 5
equivale
x = log 2 5 ←

→ 2 x = 5
In questo esempio la base del logaritmo è 2 , l’argomento del logaritmo è 5 . Si può generalizzare il
ragionamento fatto introducendo una base qualunque a e un argomento qualunque b, cosa che porta alla
definizione più generale di logaritmo data nella pagina seguente.
I logaritmi parte prima – pag. 1 di 3
DEFINIZIONE DI LOGARITMO
IL LOGARITMO IN BASE a DI b
x
È QUEL NUMERO x TALE CHE a = b
equivale
x = log a b ←

→ a x = b
La base a deve soddisfare alle condizioni 0 < a < 1 ∨ a > 1
L’argomento b deve soddisfare la condizione b > 0
………………………………………………………………………………………………………………
Dalla definizione data dovrebbe essere chiaro che il logaritmo è un esponente. Alcuni logaritmi possono
essere calcolati semplicemente passando dalla equazione logaritmica a quella esponenziale.
Esempi:
x = log 3 9 → 3 x = 9 → 3 x = 32
→
x=2
Possiamo quindi dire che log 3 9 = 2 , dato che 32 = 9
………………………………………………………………………………………………………………
1
1
x = log 5
→ 5x =
→ 5 x = 5 − 2 → x = −2
25
25
1
1
Quindi log 5
= −2 , dato che 5−2 =
25
25
………………………………………………………………………………………………………………
3
x = log 6 5 216
→ 6 x = 5 216
→ 6 x = 5 63
→
6x = 65
→
x=
3
5
3
3
, dato che 6 5 = 5 216
5
………………………………………………………………………………………………………………
Quindi log 6 5 216 =
Esercizi per lo studente diligente:
sul libro di testo pag. 71
o numeri 24-25-26-27
o numeri 33-34-35-36-37
o numeri 41-42-43-44
………………………………………………………………………………………………………………
I logaritmi parte prima – pag. 2 di 3
PRIME PROPRIETÀ DEI LOGARITMI
Dalla definizione di logaritmo seguono immediatamente le proprietà seguenti, da
ricordare a memoria.
………………………………………………………………………………………………………………
1a PROPRIETÀ DEI LOGARITMI
log a 1 = 0
DIMOSTRAZIONE
x = log a 1 → a x = 1 → a x = a 0
→
x=0
ossia
log a 1 = 0
QED♦
………………………………………………………………………………………………………………
2a PROPRIETÀ DEI LOGARITMI
loga a = 1
DIMOSTRAZIONE
x = log a a → a x = a → a x = a 1
→
x =1
ossia
log a a = 1
QED
………………………………………………………………………………………………………………
3a PROPRIETÀ DEI LOGARITMI
loga a n = n
DIMOSTRAZIONE
x = log a a n
→ ax = an
→ a x = an
→
x=n
ossia
log a a n = n
QED
………………………………………………………………………………………………………………
♦
Quod Erat Demonstrandum
I logaritmi parte prima – pag. 3 di 3