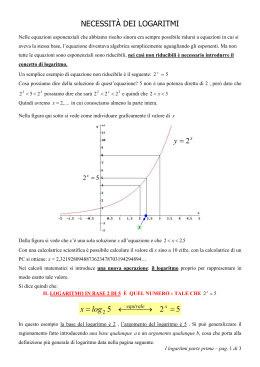
SCALE LOGARITMICHE
Se si vogliono rappresentare su una retta numeri (reali positivi) che hanno un campo di
variazione molto vasto (per esempio le frequenze di udibilità del suono o le distanze
interstellari) si ricorre a una scala logaritmica, ovvero si considera, al posto del numero, il suo
logaritmo decimale.
Infatti, se un numero è maggiore di 10, il suo logaritmo decimale è molto più piccolo del
numero stesso:
se 0 < x < 1
log x < 0
se 1 ≤ x < 10
0 ≤ log x < 1
se 10 ≤ x < 100
1 ≤ log x < 2
se 100 ≤ x < 1000
2 ≤ log x < 3 …………..
Per costruire una scala logaritmica sulla retta dei numeri, si fissano un punto O come origine e
un segmento u come unità di misura. Nella figura seguente, in blu sono rappresentati i numeri
e in rosso i loro logaritmi decimali.
Al punto O si fa corrispondere 1 (=100), perché log 100 = log 1 = 0 . A destra di O, al punto che
si trova a distanza 1 da O si associa la potenza 101=10, perché log101 = 1 , al punto che si
trova a distanza 2 da O si fa corrispondere la potenza 102=100, perché log102 = 2 e si
prosegue così. A sinistra di O si procede in modo analogo, ma con le potenze ad esponente
negativo di 10. Per i valori intermedi si calcola in modo approssimato il corrispondente valore
del logaritmo.
Nel sistema di riferimento cartesiano, si può fissare una scala logaritmica su entrambi gli assi e
si parla in questo caso di coordinate logaritmiche. Tra le coordinate logaritmiche (X,Y) di un
generico punto P del piano e le sue coordinate cartesiane (x,y) ci sono le relazioni X=logx e
Y=logy.
Vediamo come l'uso delle coordinate logaritmiche modifichi la rappresentazione grafica di
alcune funzioni.
2
Se ad esempio vogliamo rappresentare la curva di equazione y = x 3
coordinate cartesiane è mostrata nel grafico seguente
con x>0, che in
prendiamo i logaritmi decimali dei due membri e otteniamo
2
log y = log x 3
log y =
2
log x
3
e infine, ponendoci in un sistema di coordinate logaritmiche,
2
Y = X , che è l'equazione di una retta passante per l'origine.
3
Se invece partiamo da una retta non passante per l'origine che in coordinate logaritmiche ha
equazione Y = −X + 1 e vogliamo rappresentarla in coordinate cartesiane, sostituiamo logx al
posto di X e logy al posto di Y, ottenendo:
log y = − log x + 1
log y = log x −1 + log10
log y = log
10
x
E quindi, eguagliando gli argomenti, y =
10
, che è l'equazione di una iperbole equilatera.
x
Si possono utilizzare anche coordinate semilogaritmiche, cioè un sistema di riferimento in cui
su uno degli assi, per esempio quello delle ascisse, si mantiene una scala lineare e sull'altro si
fissa una scala logaritmica; dunque X = x e Y = log y
In queste coordinate, per esempio, la funzione y = 100 ⋅ 3 x diventa
log y = log(100 ⋅ 3 x )
log y = log 100 + log 3 x
Y = 2 + X log 3
Mentre la funzione Y = X log 6 + log 3 diventa log y == log(3 ⋅ 6 x ) cioè y = 3 ⋅ 6 x .
ESERCIZI
1. Fissare un sistema di riferimento logaritmico, ponendo 0, 1, 2, 3, 4, 5 sull'asse delle
ascisse e 1, 10, 100, 1000, 10000 sull'asse delle ordinate. Individuare i punti A(2, 90) e
B(4, 6000). La retta passante per A e B rappresenta il grafico della funzione esponenziale
y = b ⋅ ax . Trovare i valori di a e di b.
2. In un grafico con scala semilogaritmica sono rappresentate le rette di equazioni:
a.
Y = − log 2 + (log 3)X
b.
Y = − log 3 + (log 4)X
Trovare il legame funzionale tra x e y dove X=x e Y=logy.
Determinare il coefficiente angolare della retta che rappresenta, su tale scala, la funzione
x
1
y=  .
3
3. In un grafico con scala logaritmica sono rappresentate le rette di equazioni
a.
Y = −3X + 5
b.
Y = log 5 +
3
X
2
Trovare in entrambi i casi il legame funzionale tra x e y.
4. Rappresentare graficamente lo spettro di frequenze elettromagnetiche, a partire dalle onde
radio fino alla radiazione γ .