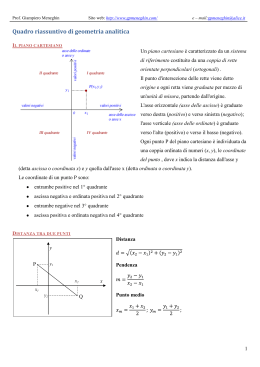
Cosa è un luogo?
Si definisce luogo geometrico l’
insieme di tutti e soli i punti
che godono di una certa
proprietà detta proprietà
caratteristica del luogo
Se in un piano è assegnato un
R.C.O., al luogo geometrico si
associa in modo biunivoco un’
equazione algebrica in x ed y che
rappresenta il legame tra l’ ascissa
e l’ ordinata di ciascun punto del
luogo
Consideriamo in un piano un riferimento
cartesiano ortogonale xOy.
Una retta del piano può assumere
diverse posizioni rispetto al sistema di
riferimento.
Analizziamo i casi in cui la retta sia
parallela agli assi
RETTA PARALLELA ALL’ ASSE DELLE ASCISSE
Y
Consideriamo
A(0,h)
una retta r
parallela all’ asse delle ascisse
e sia A(0,h) il punto in cui essa
interseca l’ asse delle ordinate.
Osserviamo che
che è quindi il luogo geometrico dei punti del
piano di ordinata h.
Ne segue che tutti i punti di r hanno coordinate
che soddisfano l’ equazione y=h.
RETTA PARALLELA ALL’ ASSE DELLE ORDINATE
y
Analogamente, nel caso in
cui
la
retta
risulti
parallela all’ asse delle
ordinate ed intersechi l’
asse delle ascisse in un
punto B(k,0), tutti i suoi
punti avranno la stessa
ascissa K e viceversa un
punto del piano di ascissa
K deve necessariamente
appartenere alla retta.
B(k,0)
x
L’ equazione di tale retta
sarà quindi
In particolare l’ asse delle
ordinate avrà equazione
RETTA IN POSIZIONE GENERICA
Consideriamo ora una retta non parallela agli assi. Su tale
retta prendiamo due punti distinti A(xA,yA) e B(xB,yB)
y
x
Condizione necessaria e sufficiente affinché un punto P(x,y)
appartenga alla retta AB è che esso sia allineato con A eB
cioè se e solo se i triangoli ABH e APH risultano simili , cioè
yP  yA yB  yA

xP  xA xB  xA
Condizione di allineamento di tre punti
yP-yA
yB-yA
xB-xA
xP-xA
Sostituendo le coordinate di P:
yP  y
yB  yA

xP  xA xB  xA
y  yA
x  xA

O anche
xB  xA yB  yA
Nell’ equazione
y  yA
yB  yA

x  xA xB  xA
Moltiplicando a croce, semplificando i termini opposti e
portando tutto al primo membro si ottiene
(yA-yB)x+(xA-xB)y+xAyB-yAxB=0
Ponendo:
a=(yA-yB)
b=(xA-xB)
e c= xAyB-yAxB
L’equazione precedente diventa ax+by+c=0
L’ equazione
y  yA
x  xA

xB  xA yB  yA
Permette di determinare l’ equazione della retta
passante per due punti A e B note le coordinate dei
punti
Si può dimostrare anche che ogni
equazione in due variabili
(con a  b  0)
2
2
rappresenta una retta i cui punti hanno
coordinate che soddisfano l’ equazione
stessa