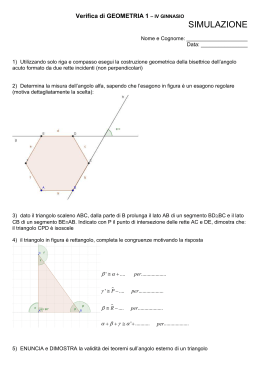
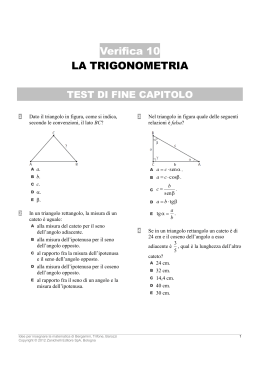
Teoremi sulle disuguaglianze dei triangoli
In un triangolo a lato maggiore si oppone angolo maggiore
A
HP
AC>AB
TH
β>δ
β
α
B
D
α
δ
C
Poiché AC>AB prendiamo un segmento AD=AB sul lato AC, otteniamo un triangolo
isoscele ABD sulla base BD.
L’ angolo ADB>DCB perché ADB è angolo esterno del triangolo BDC, pertanto α>δ
Ma β>α perché è una sua parte segue che β>δ per la proprietà transitiva.C.V.D.
In un triangolo un lato è minore della somma degli altri due ed è
maggiore della loro differenza.
D
α
HP
ABC triangolo
TH
BC<AB+AC
AB>BC-AC
A
β
α
B
C
L’ angolo β>α perché α è una sua parte ,pertanto per il teorema precedente il lato
CD> BC , infatti CD si oppone all’ angolo maggiore.
CD > BC, ma CD=AC+AD, sostituiamo con segmenti congruenti e otteniamo AC+AD>BC
e sostituendo ancora otteniamo AC+AB>BC. C.V.D.
Esiste un triangolo con lati di misura : 4cm,5cm,8cm?
Esiste un triangolo con lati di misura : 3cm,5cm,9cm?
Esiste un triangolo con lati di misura : 3cm,5cm,6cm?