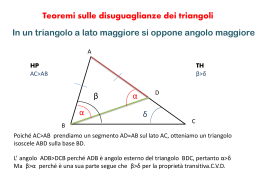
Problema n. 46 pag. 190
Nel triangolo ABC si sa che cos(BAC)=cos=7/25 e tg(ABC)=tg =4/3 , CM=a, essendo CM l’altezza relativa
ad AB.
Determinare:
a)
b)
c)
d)
e)
Le funzioni goniometriche di , e quelle di ACB=;
Le misure dei lati del triangolo ABC
Le altezze relative ai lati AC e CB
La distanza dell’ortocentro H dal lato AB
Le funzioni goniometriche di MBH
a) cos  
cos  
1
1
16
9
49 24
49 24
7
sin   1 

tg  1 

25
625 25
625 7

3
5
sin   1 
9 4
4

tg  
3
5 5
cos   cos(180  (   ))   cos(   )   cos  cos   sin  sin   
sin   1 
9 4
9 4

tg  1  
5 5
5 3
b) AC 
AM 
21 96
75 3



125 125 125 5
CM
a 25
CM
a 5


a CB 
  a
24
sin 
24
sin  4 4
25
5
CM
a
7


a
tg 24 24
7
BM 
CM a 3
  a
tg  4 4
3
AB 
7
3
25
a a 
a
24
4
24
25 24
25 4
5
a  a AE  AB sin  
a a
24 25
24 5
6
CM
a
7
7
1
7 1 7
d) AM 


a HM  AM  tg (90   )  a
 a  a
tg 24 24
24 tg  24 4 32
7
3
e) cos HBM  cos(90   )  sin  sin HBM  sin(90  )  cos 
c)
BD  AB sin  
tgHBM  tg (90   ) 
1
tg
Problemi n. 47 pag. 190
Dato il trapezio ABCD, avente:
A=D=90°, cos(BCD)=-3/5 ; BC=20; DC=10
Determinare il perimetro 2p e l’area S.
cos   
4
9 4
3
tg  
sin   1 

3
5
25 5
4
CH  CB sin(180   )  CB sin   20  16
5
3
BH  CB cos(180   )  CB cos   20  12
5
AB  BH  AH  12  10  22
P  22  20 10 16  68
Area 
22  10
16  256
2
Problemi n. 51 pag. 191
Data la semicirconferenza di centro O e diametro AB=2r, condurre per O la perpendicolare ad AB e
prendere su di essa un punto C e tale che OC=2r. Condurre da C le tangenti alla circonferenza fino a
incontrare in E ed F i prolungamenti di AB. Detto T il punto di tangenza di CE con la semicirconferenza,
determinare su EF un punto P in modo che PT=minimo e PT massimo.
Intanto calcoliamo gli angoli e i lati della figura.
sin  
OT
r 1


  30
OC 2r 2 da cui
OE 
Allora
OT
r
2


r
cos 
3
3
2
TH  OT sin  
FE 
4
3
r TE  OTtg  
r
3
3
r
2
3
3
2
3
2 3
7 3
r TH 
r
r
r
r
r
2
2
2
3
6
3
OH  OT cos  
147 2 r 2
147  9 2
13
TF  FH  TH 
r  
r 
r
36
4
12
3
2
2
Posto PTE=x
PT
TE
3 3
r
r

PT 

sin 60 sin(120  x)
3 2 sin(120  x) 2sin(120  x)
Il massimo del sino è a 90° e quindi stando a denominatore ottengo i minimo quando
120-x=90 cioè quando x=30° e quindi quando P coincide con H.
Problemi n. 52 pag. 191
E’ dato il triangolo ABC, isoscele sulla base AC; l’angolo alla base ha il coseno uguale a 12/13 e l’altezza AH
relativa al lato BC misura a. Calcolare i lati del triangolo e classificarlo rispetto agli angoli. Detto I
l’ortocentro del triangolo, calcolare le distanze I dai vertici del triangolo.