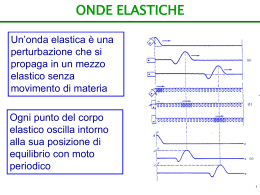
1. Le onde elastiche
1.5-7 Equazioni delle onde
1.5 Le onde periodiche

Onda periodica: sorgente oscilla senza fermarsi

Periodo T: tempo che un punto impiega per un’oscillazione completa

Frequenza f: numero di oscillazioni che compie nell’unità di tempo

Risulta

Se il moto della sorgente è armonico,
si ottengono onde armoniche:
ogni punto del mezzo oscilla con lo stesso
periodo T e la stessa frequenza f
f 
1
T
1.5 Le onde periodiche



Lunghezza d’onda λ: distanza tra due creste (o tra due gole) =
spazio percorso dall’onda in un periodo
Ampiezza: massimo spostamento di un punto dalla posizione di
equilibrio

v
Velocità dell’onda
T
per una corda di tensione F e densità lineare ρ
v
F

1.5 Equazioni delle onde armoniche

Equazione dell’onda in un punto al variare del tempo t
y  a cos t  0 
dove,
y è la grandezza che oscilla,
a è l’ampiezza,
ω = 2π / T = 2πf è la pulsazione e
φ0 è una costante, detta fase iniziale,
tale che y(t=0) = a cosφ0

Equazione dell’onda a un certo istante di tempo, al variare della
posizione x
(fotografia dell’onda a un istante t)
 2

y  a cos
x  0 
 

1.6 Il principio di sovrapposizione

Quando due onde si incrociano nello
stesso punto, esse si attraversano senza
disturbarsi:
la oscillazioni causate da ciascuna onda si
sommano tra loro e la perturbazione che
ne risulta è data dalla somma delle
perturbazioni che ciascuna onda
produrrebbe singolarmente
(principio di sovrapposizione)
1.7 L’interferenza


Due o più onde che si sovrappongono in una stessa zona dello spazio
Consideriamo l’interferenza di due onde armoniche della stessa
frequenza
y1  a cos t  ;
y2  a cos t  0 
applicando le formule di prostaferesi
 

cos   0 
2
2

si ottiene un nuovo moto armonico con la stessa frequenza ω, fase
φ0/2 e ampiezza A = 2acos φ0/2.
Il risultato dell’interferenza dipende dallo sfasamento delle due onde
se φ0 = (2k + 1)π, allora A=0 e l’interferenza si dice distruttiva
se φ0 = 2kπ, allora A=2a e l’interferenza si dice costruttiva
y  y1  y2  2a cos

1.
2.
0