OSCILLAZIONI
ONDE
Applicazioni mediche degli
ultrasuoni
1
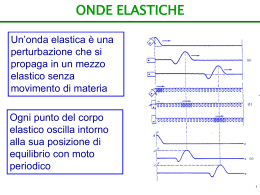
MOTI OSCILLATORI
2
Moto armonico semplice
Compare the motion of these two balls.
Uniform Circular Motion
(radius A, angular velocity w)
Simple Harmonic Motion
(amplitude A, angular frequency w)
3
x
4
5
6
7
Oscillazioni smorzate
8
9
Ponte di Tacoma: venti stazionari innescano
oscillazioni stazionarie (a) e il trasferimento risonante
di energia porta la struttura al collasso (b)
10
ONDE
11
12
13
Propagazione ondulatoria
14
15
16
17
Velocità di fase nei mezzi





In generale la velocità di propagazione nei mezzi dipende dalle
proprietà elastiche ed inerziali degli stessi secondo la relazione:
v = [(proprietà elastiche)/(proprietà inerziali)]½
Ad esempio, per una corda sottile è:
v = √(T/m)
dove T è la tensione elastica e m la densità lineare (m/l)
Per un mezzo materiale la velocità sarà:
v = √(B/ρ)
dove B è il modulo elastico e ρ la densità.
Nel caso della propagazione in aria il mezzo gassoso risponde
elasticamente solo a compressioni, per cui per B va assunto il
modulo di compressione adiabatico:
B = γp0
e la velocità del suono dipenderà anche dalla temperatura:

18
Onde trasversali e longitudinali
trasversali
vibrazione
propagazione
esempio :
onda lungo una corda
longitudinali
vibrazione
propagazione
esempio :
onda di percussione in un solido
19
Intensita’ di un’onda
Intensità = energia trasportata nell'unità di tempo
attraverso l’unita’ di superficie
E
I =
DtS
joule
watt
=
unità di misura:
2
s m
m2
onda sferica: S=4pr2
L’energia é costante (cons.energia)
L’intensità diminuisce
con il quadrato della distanza
S
S
r
2r
20
Impedenza d’onda

Se supponiamo che l’energia trasportata
dall’onda sia quella di un oscillatore
meccanico:
E = (½)kA2 = (½)mw2A2 [ w = (k/m)½]
 L’intensità dell’onda sarà espressa da:
 I = E/(SΔt) = ½ρVω2A2/(SΔt) V = SΔh
 I = ½ρω2A2Δh/Δt = ½ω2A2ρc
 I = ½Zω2A2
( c = Velocità di fase)
 Z = ρc (impedenza d’onda)

21
Il suono
suono : vibrazione meccanica delle particelle di
un mezzo materiale (gas, liquido, solido)
punto di equilibrio
molecola in moto
A
fluidi :
x(t)
spostamenti delle particelle
addensamenti e rarefazioni
compressioni e dilatazioni
sono vibrazioni
di/tra molecole:
serve la materia!
nel vuoto
il suono
non si propaga
onda di pressione
22
Onde di compressione longitudinali
23
Caratteristiche del suono
onda sonora : vibrazione meccanica percepibile
dal senso dell'udito (orecchio)
sensibilità orecchio umano
20 Hz < n < 2•104 Hz
infrasuoni
v=ln
ultrasuoni
varia = 344 m/s
{
vacqua = 1450 m/s
Caratteristiche
di un suono:
17.2 m < l < 1.72 cm
72.5 m < l < 7.25 cm
altezza  frequenza
timbro  composizione armonica
intensità  E/(S•t)
24
Velocità, impedenza d’onda e coefficiente di riflessione
25
26
Riflessione e trasmissione nelle discontinuità
27
Riflessione e trasmissione di un impulso a varie
interfacce
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Onde elettromagnetiche


Onda elettromagnetica:
E
Eo

B
“vibrazione”
del campo elettrico
e del campo magnetico
in direzione
perpendicolare a entrambi

v

Bo
l


E

x
Una carica elettrica in moto
emette o assorbe
onde elettromagnetiche
quando soggetta ad accelerazione
Eo

B

Bo
T
t
Non serve materia: i campi
si propagano anche nel vuoto!
42
Velocita’ della luce
Le onde elettromagnetiche si propagano
anche nel vuoto
secondo la consueta legge:
ln = v
La loro velocità nel vuoto è sempre
c = 3•108 m/s
(= 300000 km/s)
E’ la velocità della luce
ma anche di tutte le altre onde elettromagnetiche.
E’ la massima velocità raggiungibile in natura.
Nei mezzi materiali la velocità è c/n (<c).
43
44
Interferenza
45
Interferenza costruttiva
46
Interferenza distruttiva
47
Interferenza tra onde di diversa
ampiezza
48
49
50
51
Oscillazioni stazionarie
52
Primi tre modi propri stazionari per un sistema chiuso
53
Primi tre modi propri stazionari per un sistema chiuso
L = l/2
l = 2L
f = v/(2L)
L=l
l=L
f = v/(L)
L = 3l/2
l = 2L/3
f = 3v/(2L)
54
Condotto aperto
Per un sistema aperto ad entrambe le estremità, i primi
tre modi vibrazionali sono:
55
Condotto semiaperto: prime tre armoniche dispari
L = l/4
l = 4L
f = v/(4L)
L = 3l/4
l = 4L/3
f = 3v/(4L)
L = 5l/4
l = 4L/5
f = 5v/(4L)
56
SOVRAPPOSIZIONE DI OSCILLAZIONI DI DIVERSA
FREQUENZA
57
Battimenti
58
Teorema di Fourier
Qualsiasi funzione periodica y(t) di periodo T
può essere scritta come:
y(t) = Sn [An sin(2pfnt + fn) + Bncos(2pfn+ fn)]
Dove f1 = 1/T and fn = nf1
-Jean Baptiste Joseph Fourier
59
Sintesi di funzioni sinusoidali semplici
60
Sintesi dell’oscillazione “dente di sega”
61
Sintesi di un’onda quadra
62
Modi di vibrazione di una lastra piana
Modo a 73 Hz
Modo a 82 Hz
Modo a 142 Hz
63
Primi quattro modi di vibrazione della membrana di un tamburo
64
Forma d’onda e spettrogramma del suono di un tamburo
65
Forme d’onda e spettri di strumenti musicali
66
Differenze spettrali
67
Effetto Doppler
68
Emissione di onde da una sorgente ferma (sx)
e da una in movimento (dx)
Fig.1: Onde prodotte da sorgente fissa
Fig. 2: Onde prodotte da sorgente mobile
69
Effetto Doppler

Un ricevitore R rivela un segnale ondulatorio alla stessa
frequenza con cui è stato emesso da una sorgente S?

L’effetto Doppler ci dice che questo è possibile solo se S
ed R sono in quiete relativa l’uno rispetto all’altro.

In caso contrario, detta VR la velocità del rivelatore, VS la
velocità della sorgente e C la velocità di propagazione
dell’onda, la frequenza FR percepita dal rivelatore e la
frequenza FS emessa dalla sorgente sono legate dalla
seguente relazione:
 FR = [( C ± VR ) ∕ ( C ∓ VS )]FS
70
Sonogrammi Doppler
Fig.3: Sonogramma di un clackson
Fig. 4: Sonogramma di un aereo
71
72
73
Flussimetria Doppler

L’impulso ultrasonoro incide sul fronte della mandata sanguigna che si
muove con velocità v. La frequenza effettiva ricevuta è (sorgente ferma –
ricevitore in moto):
F’ = F(1±v/c)

L’impulso riflesso viene generato ad una frequenza F’ da una sorgente in
moto e rivelato da un ricevitore fermo:
FD = F(1±v/c)(1∓v/c)-1


Nel caso in cui v/c≪1, verificato in quanto c=1500m/s e v≲1m/s,(1∓v/c)-1
può essere sviluppato in serie di potenze ed è:

Pertanto:
(1∓v/c)-1 ≂ (1±v/c)

FD = F(1±v/c)2 ≂ F(1±2v/c) ; FD-F = ΔF = ±(2v/c)F
ΔF viene denominato “shift Doppler” e consente di risalire alla velocità
(negli apparecchi detti “bidirezionali” anche al segno) del bersaglio
 Generalmente ΔF viene rivelata filtrando la frequenza di modulazione dei
battimenti generati dalla sovrapposizione dell’eco (shiftato Doppler) con il
segnale del generatore.

74
Dipendenza di v dall’angolo di incidenza
‫דר‬

‫מש‬
V
‫מהירות‬
‫הזורם‬
Δf  C
V=
2f 0 cos θ
75
Schema di un (antiquato) apparecchio Doppler
76
77