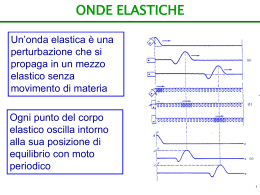
7
La propagazione
elle onde
Q
mediante un moto ondoso.
La parola «onda" ci fa subito
pensare alle onde del mare.
Tuttavia molti fenomeni in
apparenza diversi hanno a
che fare con le onde, per
esempio il suono e la luce.
In questo capitolo parleremo
delle onde sonore, nei.
prossimi della luce.
uando un corpo si
.
muove, la sua energia
meccanica si sposta da un
punto all'altro dello spazio.
Ma l'energia meccanica può
anche propagarsi senza che vi
sia spostamento di materia.
L'energia meccanica si può
trasmettere da un punto
all'altro di un mezzo elastico
,./
7.1
I SISTEMI OSCILLANTI
Nella figura 1 compaiono alcuni semplici sistemi oscillanti:
una molla, un pendolo, una lamina, una punta vibrante. Che
cosa hanno in comune?
96
Figura 1. Il pendolo
oscilla attorno alla
posizione verticale, la
massa appesa alla molla
oscilla attorno alla
posizione d'equilibrio.
L'asta vibra attorno alla
posizione orizzontale. La
punta appesa alla molla
vibra sulla superficie
dell'acqua. Tutti questi
sistemi oscillano perché
sono sottoposti a una forza
che tende a riportarli nella
posizione d'equilibrio.
7. La propagazione
delle onde
Una forza proporzionale
allo spostamento dalla
posizione di equilibrio si
chiama forza elastica.
>(Per tutti esiste una posizione di equilibrio stabile.
• Se ognuno di quegli oggetti viene spostato dalla posizione
di equilibrio, comincia a oscillare .
• Responsabile dell'oscillazione è una forza di richiamo proporzionale allo spostamento dalla posizione di equilibrio.
• Durante l'oscillazione l'energia cinetica si trasforma in potenziale e viceversa.
I sistemi oscillanti sono interessanti perché permettono di
generare delle onde, cioè delle perturbazioni che si propagano
trasportando energia ma non materia. Per esempio, la lamina
che vibra comprime gli strati d'aria quando si muove verso di
essi. Uno strato compresso preme a sua volta quello successivo e questo ne comprime un altro e così via dando origine a
una perturbazione che si propaga nel mezzo.
Le onde più semplici sono quelle sinusoidali: esse sono
generate da sorgenti che oscillano con moto armonico.
Possiamo rappresentare il moto di un'onda nel tempo (fig.,2, )
e nello spazio (fig;~. I due diagrammi hanno significato ~",<ì.t
diverso. La figura 2 mostra le successive posizioni di una
Q
particella del mezzo elastico, per esempio una molecola di
acqua, al trascorrere del tempo (quando è investita da
un'onda). La figura 3 mostra la posizione delle particelle del
mezzo in un dato istante (fotografia dell'onda).
o
'C
@
'3
cr
~
-;;;
-c
o
~ O~------*-------~------~-------.~----~
E
~o
o.
'"
posizione
o
'C
g
'3
cr
~
-;;;
. -c
o
c
i
o
5l-
Figura 2. Grafico che
rappresenta lo spnstamento delle molecole d'acqua
(e in generale delle
particelle di un mezzo
elastico) a un determinato
istante di tempo, quando
sono raggiunte da un'onda
sinusoidale. Il grafico
equivale a una fotografia
istantanea di una sezione
trasversale dell'acqua:
si «vedono •• molecole sul
pelo dell'acqua (a livello
O), sopra e sotto. Le
molecole che distano una
(o più) lunghezze d'onda À
hanno lo stesso spostamento e si muovono nello
stesso modo.
Figura 3. Grafico che
rappresenta lo
spostamento di una
molecola d'acqua (e in
generale di una particella
di un mezzo elastico) in
funzione del tempo,
quando è raggiunta da
un'onda sinusoidale. In
ogni intervallo di tempo
O'--------~------~--~--~------~~----~uguale
a un periodo (T) la
molecola va su e giù,
compiendo un'oscillazione
completa intorno alla
posìztone di equilibrio.
tempo
97
ACUSTICA
7.2
LE ONDE
Le grandezze che caratterizzano un'onda sono:
• il periodo (T): tempo impiegato a compiere un'oscillazione completa (fig. 2);
• la frequenza (f): numero di oscillazioni complete in un
secondo;
• la lunghezza d'onda (À): distanza percorsa in un periodo
(fig. 3);
• la velocità di propagazione (v): rapporto fra distanza percorsa e tempo impiegato;
• l'ampiezza (a): massimo spostamento subito da un punto
del mezzo;
Equazione fondamentale di un'onda:
lunghezza d'onda
velocità = ---'-----periodo
À
L'equazione è valida per
ogni tipo di onda.
Un mezzo è elastico se,
sottoposto a uno sforzo,
subisce una
deformazione. Quando la
causa della deformazione
cessa, il mezzo riassume
la configurazione iniziale.
v=-.
T
Tipi di onde
Esistono due tipi di onde: quelle meccaniche e quelle elettromagnetiche. In questo capitolo studiamo le onde che si propagano in un mezzo elastico: le onde meccaniche.
Sia i corpi solidi sia i fluidi sono più o meno elastici perché,
entrambi sottoposti a delle forze, subiscono deformazioni.
Perciò le onde si propagano sia nei solidi sia nei fluidi.
Distinguiamo due tipi di onde meccaniche, quelle longitudinali e quelle trasversali.
Le onde longitudinali sono quelle in cui le particelle del
mezzo oscillano nella direzione in cui si propaga 1'onda. Per
esempio, se comprimiamo alcune spire di una molla vincolata
a un estremo e poi le lasciamo andare, nella molla si propaga
un impulso longitudinale (fig. 4a).
Figura 4. Onda longitudi·
naie su una molla (a),
fotografata a tre istanti
di tempo successivi.
Ciascun punto della molla
si muove avanti e indietro
in orizzontale, nella stessa
direzione in cui si propaga
l'onda. Onda trasversale
su una molla (b), totnarafata a tre istanti di tempo
successivi. Ciascun punto
della molla si muove in
alto e in basso in verticale,
in direzione perpendicalare a quella in cui si
propaga l'onda.
t2 h/'V\/l,/\J\/'d"/\
98
7. La propagazione
delle onde
1
Puoi generare un'onda
trasversale stendendo
una corda per terra e
dando un impulso verso
l'alto a una estremità.
«;
7.3
Il suono non si propaga
nel vuoto.
Le onde trasversali sono quelle in cui le particelle del mezzo
oscillano in direzione perpendicolare alla direzione in cui si
propaga l'onda. Per esempio, nella figura 4b un impulso è
stato applicato alla molla in direzione perpendicolare alla direzione di propagazione, che è orizzontale.
ONDE SONORE
Il suono è una tipica perturbazione longitudinale prodotta in
un mezzo elastico (di solito l' aria) da un corpo che vibra con
una certa frequenza. Si propaga nei solidi, nei liquidi e nei gas
con velocità diversa. La velocità di propagazione dipende
dalle caratteristiche elastiche del mezzo e, per ogni mezzo, la
velocità dipende anche dalla temperatura.
Alcune velocità di propagazione del suono
velocità (m/s)
Mezzo
331
Aria
Una formula empirica è
ricavata dall'esperienza.
340
Note
~~3,ç
O°C
Acqua
1465
15°C
Ferro
5130
20 -c
Acciaio
5100
20°C
Esistono alcune formule empiriche che permettono di calcolare in modo approssimato la velocità di propagazione in funzione della temperatura. Indicando con t la temperatura del
mezzo espressa in gradi celsius, la velocità v del suono si può
calcolare con le seguenti equazioni:
= 331,5 + 0,6· t
v = 1400 + 4,2· t
nell'aria,
v
nell'acqua.
L'orecchio umano percepisce i suoni che hanno frequenza
compresa fra 16 e 20000 Hz. Si chiamano ultrasuoni quei
suoni che hanno frequenza superiore a 20 000 Hz.
Alcuni animali riescono a percepire anche gli ultrasuoni.
7.4
La potenza è l'energia
nell'unità di tempo.
INTENSITA DI UN'ONDA
È la quantità di energia che, in un intervallo di tempo unitario,
attraversa una superficie di area unitaria, disposta perpendicolarmente alla direzione di propagazione. Dato che il rapporto
fra energia e tempo è la potenza, la relazione risulta:
Intensità
Potenza
= ----
area
el Sistema Internazionale i misura in watt/m' (,vV/m2).
Poiché l'intensità è inversamente proporzionale all'area,
99
A~/2.DC
D
~ç
ACUSTICA
maggiore è l'area su cui si distribuisce l'energia, minore è
l'intensità dell'onda. Consideriamo una sorgente puntiforme
di potenza P. Poiché l'onda si propaga nello spazio in tutte le
direzioni, l'energia si distribuisce su una sfera con il centro
nella sorgente (fig. 5).
La superficie della sfera di raggio r è 411 • r 2, pertanto
l'intensità vale:
p
1=---2 .
Abbiamo già incontrato
una dipendenza di questo
tipo: la forza
gravitazionale è
inversamente
proporzionale al quadrato
della distanza.
411 •
r
L'intensità diminuisce a mano a mano che ci si allontana dalla
sorgente ed è inversamente proporzionale al quadrato della
distanza; se la distanza raddoppia l'intensità diventa 1/4, se
triplica diventa 1/9 e così via.
Figura 5. L'intensità
dell'onda diminuisce con
l'inverso del quadrato
della distanza dalla
sorgente: raddoppiando la
distanza l'intensità diventa
1/4, triplicando la distanza
l'intensità diventa 1/9". Le
circonferenze potrebbero
per esempio rappresentare
le creste delle onde che si
creano nell'acqua dopo
avervi gettato un sasso
(sorgente della
perturbazione l.
LIMITI DI UDffiIUTÀ
L'intensità dell'onda sonora più debole che l'orecchio umano
può udire prende il nome di soglia di udibilità e vale circa
1min = 1x lO
Suoni di intensità minori
di 'min non vengono
percepiti, suoni di
intensità maggiore di 'rnax
provocano dolore o danni
per l'orecchio.
7.6
Se l'onda incide in una
direzione obliqua, l'angolo
secondo cui è riflessa è
uguale all'angolo secondo
cui incide.
-16
W
:~
I
--2-'-
cm
Il suono più forte che l'orecchio può sopportare ha intensità
1m.x = 1 x lO
-6
W
..;
--2-'
cm
FENOMENI LEGATI ALIA PROPAGAZIONE
DELLE ONDE
Riflessione
Quando un'onda incontra un ostacolo, in genere viene riflessa
e torna indietro (fig. 6). Un tipico fenomeno legato alla riflessione di un'onda sonora è l'eco.
Interferenza
Quando due onde passano per uno stesso punto si sovrappongono senza deformarsi e poi proseguono nella loro direzione
100
7. La propagazione
delle onde
~
_._
..
===".".,,-~
'c
~.
Figura 5. Un'onda che si
propaga su una corda
avanza verso destra
(in alto) e viene riflessa
(in basso) dalla parete,
dove è fissata l'estremità
della corda. L'onda riflessa
appare rovesciata rispetto
all'rmda incidente.
•• i
di propagazione (principio di sovrapposizione). L'ampiezza
dell'onda risultante dipende dalla sovrapposizione in P di due
creste (onde in fase), come nella figura 7, oppure una cresta e
un ventre (onde in opposizione di fase), come nella figura 8.
el primo caso si ha interferenza costruttiva, le ampiezze si
sommano e l'ampiezza dell'onda risultante è massima; nel
secondo caso si ha interferenza distruttiva, le ampiezze si
sottraggono e l'ampiezza dell'onda risultante è minima.
Figura 7. L'impulso a e
l'impulso /J si avvicinano
(in alto), si «scontrano» (in
mezzo), poi si allontanano
(in basso) riprendendo la
forma iniziale. Mentre si
«scontrano» i due impulsi
interferiscono in modo
costruttivo: poiché
entrambi sono positivi, si
rinforzano dando luogo a
un'impulso che ha
ampiezza uguale alla
somma delle ampiezze di
a eh.
~=========-~-~
l.
Figura B. Gli impulsi a e
h, che si avvicinano (in
alto), si «scontrano» (in
mezzo), poi si allontanano
(in basso), sono l'uno
l'opposto dell'altro.
Mentre si «scontrano» i
due impulsi interferiscono
in modo distruttivo,
annullandosi: per un
istante la corda appare
orizzontale, come se non
fosse perturbata.
b~
ti
••
Effetto Doppler
Se una sorgente sonora ferma emette un suono di una certa
frequenza, un osservatore fermo riceve un suono con la stessa
frequenza.
Quando una sorgente sonora emette un'onda e nello stesso
tempo si muove rispetto a chi percepisce l'onda, la frequenza
101
ACUSTICA
percepita è diversa dalla frequenza emessa: questo fenomeno
prende il nome di effetto Doppler (fig. 9). Indicando con fa la
frequenza emessa dalla sorgente e confla frequenza percepita
dall'osservatore valgono le due formule:
f = fa'
f
In generale, l'effetto
Doppler si ha quando vi
è un movimento relativo
fra la sorgente sonora e
l'osservatore.
Se l'osservatore si
avvicina percepisce una
frequenza maggiore
(suono più acuto), se si
allontana una frequenza
minore (suono più grave).
v
v -
se la sorgente si avvicina all'osservatore,
Vs
v
= fa'
se la sorgente si allontana dall'osservatore.
v + Vs
Vs è la velocità della sorgente sonora e v la velocità di propagazione del suono.
.L'effetto Doppler si ha anche quando l'osservatore si
muove rispetto a una sorgente ferma (fig. lO). Indicando con
Vo la velocità dell'osservatore,
la frequenza che egli percepisce è data da
f
f
i + Vo
= fa . --
v
~
'~-v
= fa . __
o
quando si avvicina alla sorgente,
quando si allontana dalla sorgente.
v
--...J
f=1o(~+~)
~~tC~-~)
Figura 9. L'ambulanza è
ferma (a), la sirena emette
delle onde sonore.
All'uomo e alla donna
arrivano con la stessa
lungheua d'onda À. (b),
quindi entrambi sentono
lo stesso suono.
t
Figura 10. Quando
l'ambulanza si muove (a),
le onde sonore emesse
dalla sirena non sono più
concentriche ma appaiono
schiacciate nel senso del
movimento. Infatti, poiché
la sirena si muove verso
destra, anche i centri delle
onde si spostano verso
destra (b): l'onda A è stata
emessa quando la sirena
si trovava in a, l'onda B
quando la sirena si trovava
in b e cosi via. Pertanto la
donna percepisce un suono
più acuto perché le onde
arrivano al suo orecchio
con una lunghezza d'onda
piccola (À. 2)' L'uomo,
invece, percepisce un
suono niù grave.
t
102