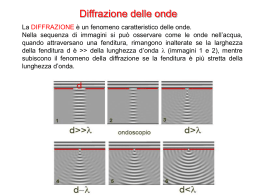
Corrente (o conteggi) di buio
Anche in assenza di luce i PMT producono una piccola
corrente (e manifestano dei picchi)
Le cause principali sono:
• Emissione termica di elettroni dal fotocatodo e dai
dinodi (fattore dominante).
• Raggi cosmici
• Corrente ad emissione di campo
• Correnti di perdita
Corrente (o conteggi) di buio
Aumenta con voltaggio applicato e T
Problema
PMT
Fattore di risposta
• I PMT hanno una
risposta molto
dipendente dalla
lunghezza d’onda
1
0
300
400
(nm)
500
600
Rivelatore di riferimento:
“quantum counter”
•Per ovviare alla dipendenza della
sensibilità del PMT da , si usa un
trucco.
•Una soluzione di rodamina (di
solito B), estremamente
concentrata (3-8 g/L), assorbe
tutta la luce incidente
(assorbimento totale)
•La fluorescenza emessa è
proporzionale alla luce incidente
(indipendentemente dalla sua
exc.)
•La fluorescenza emessa ha una
lunghezza d’onda fissa
(indipendentemente dalla exc.).
Assorbanza o Fluorescenza
Rodamina B
200
300
400
500
600
700
 (nm)
250-600 nm
4%
Rivelatore di riferimento:
fotodiodo
In un semiconduttore, un fotone può far passare gli
elettroni dalla banda di valenza a quella di conduzione,
creando una corrente.
•Molto meno sensibile dl PMT
•Più lento del PMT
•Compatto, piccolo, resistente
•Non richiede HV
•Alcuni hanno una dipendenza da  molto piccola
Fotodiodo
Fattore di risposta
1
0
300
400
(nm)
500
600
Monocromatore
Onde monocromatiche
• Un’onda elettromagnetica è costituita da un campo elettrico e
magnetico oscillanti nel tempo e nello spazio.
• E e B non sono indipendenti:
– sono perpendicolari tra loro ed alla direzione di propagazione
dell’onda.
– I loro moduli sono collegati dalla relazione: B   E
• È sufficiente il campo elettrico per definire l’onda.
E ( z, t )  E0 cos2 t  cz 
x
z
y
Somma di due onde e interferenza
• Se devo considerare la sovrapposizione di due onde (della stessa
frequenza), bisogna tener conto che non sono necessariamente in
fase:
 E1 ( z , t )  E10 cos2 t  cz   1 

0
E
(
z
,
t
)

E
 2
2 cos2 t  cz   2 
E1 ( z, t )  E2 ( z, t )  E10 cos2 t  cz   1   E20 cos2 t  cz   2 
Rappresentazione complessa della radiazione elettromagnetica
Il campo elettrico corrisponde alla parte reale del numero
complesso:
Ek0ei2 t  cz k 


Ek ( z , t )  Re Ek0ei2 t  cz k  
 Ek0 Recos2 t  cz   k   i sin 2 t  cz   k  
 Ek0 cos2 t  cz   k 
In questo modo la sovrapposizione di due onde si esprime in
modo molto più conciso (trascurando in genere di scrivere
esplicitamente che si considera solo la parte reale):
E1 ( z , t )  E2 ( z , t )  E10ei 2 t  cz 1   E20ei 2 t  cz 2  

 ei 2 t  cz  E10ei1  E20ei2

La diffrazione della radiazione
Per oggetti di dimensione d>> vale l’ottica geometrica (la luce si propaga in linea retta).
Oggetti di dimensione paragonabile a  diffrangono la radiazione in tutte le direzioni.
Diffrazione da parte di una serie di centri scatteranti puntiformi equispaziati
• Consideriamo una serie di punti equispaziati (con passo a).
• Inviamo su di essi una radiazione monocromatica, incidente in modo normale (per
semplicità).
• Ognuno dei puntidiffrange la luce in tutte le direzioni.
• Le radiazioni diffratte da ciascuno dei punti interferiscono.
• L’interferenza dipende dalla direzione di propagazione.
• Calcoliamo il campo elettrico totale ad un angolo q rispetto alla direzione incidente
Schermo
o
rivelatore
a
q
Diffrazione da parte di una serie di centri scatteranti puntiformi equispaziati
• Indichiamo con 0 il punto centrale, e numeriamo gli altri con interi positivi o negativi
• La differenza di cammino ottico per le onde diffratte dal punto k e dal punto 0 è data
da:
 ka sin q
2
1
0
-1
-2
a
q
q
Diffrazione da parte di una serie di centri scatteranti puntiformi equispaziati
• Il ritardo di fase è quindi dato da:
 ka sin q

2
• Il campo elettrico totale dato dall’interferenza di tutte le onde è:
E (q )  E 0
N
e
a
i 2k sin q

k  N
• La diffrazione di tutti i punti è in fase solo per:
a

sin q  intero
Sviluppiamo la sommatoria
E (q )  E
0
N
e
a
i 2k sin q

0  ( N 1) b
E e
2 N 1
k  N
e
k 1
kb
b  i 2
a

sin q
b
( 2 N  2)b
e

e
E (q )  E 0e  ( N 1)b

b
1 e
 Nb
( N 1) b
e

e
0e
 E0

E
1  eb
E
0
e
 ( 2 N 1) i
e
 i
a

a

sin q
sin q
e
e
a


sin  M sin q 


 E0 
 a

sin  sin q 
 

 ( 2 N 1)
b

e 2
( 2 N 1) i
i
a

b
2
sin q
a

e
( 2 N 1)
b
 e2
sin q
b
2

a


sin (2 N  1) sin q 

0


E
 a

sin  sin q 
 

M=numero di centri scatteranti colpiti dalla luce.
a


sin  M sin q 



f (q ) 
 a

sin  sin q 
 

I (q )  f (q ) 2
a sin q max  n
q max
 n 
 arcsin 
 a 
n 
qmax  arcsin  
 a 
La spaziatura dei massimi:
• diminuisce al crescere di a
(spaziatura dei punti)
•aumenta con 
In realtà i massimi hanno tutti la stessa intensità solo se i centri
scatteranti hanno dimensioni trascurabili rispetto a .
In realtà quello che si osserva è questo:
qmax è diverso per ogni lunghezza d’onda
(a parte per n=0)!
qmax
n 
 arcsin  
 a 
La risoluzione dipende dalle fenditure d’entrata e di uscita
Dispersione angolare
dq
D
d
a sin q  
a d sin q  d
a cosqdq  d
1
1
D

a cosq a
(q è molto piccolo)
Dispersione lineare
dy d F sin q 
dq
1
F
Dlin 

 F cosq
 F cosqDang  F cosq

d
d
d
a cosq a
F=distanza fra elemento
dispersivo e fenditura di
uscita
 1  nm
 D   mm
 lin 
Esempio: D-1=20 nm/mm
Bandwidth=FWHM= D-1s
Allargando le fenditure:
• aumenta l’intensità della
luce (quadraticamente)
• diminuisce la risoluzione