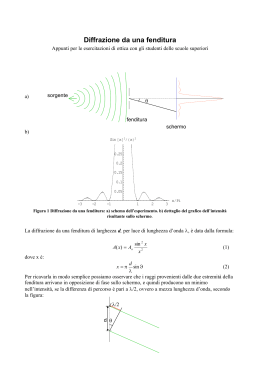
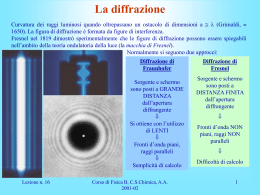
Diffrazione delle onde
La DIFFRAZIONE è un fenomeno caratteristico delle onde.
Nella sequenza di immagini si può osservare come le onde nell’acqua,
quando attraversano una fenditura, rimangono inalterate se la larghezza
della fenditura d è >> della lunghezza d’onda l (immagini 1 e 2), mentre
subiscono il fenomeno della diffrazione se la fenditura è più stretta della
lunghezza d’onda.
Diffrazione della luce
La luce è costituita da onde
elettromagnetiche. Le onde
elettromagnetiche hanno
caratteristiche simili alle onde
nei liquidi, a parte il fatto che si
propagano nel vuoto e non in
un mezzo
Il fenomeno della diffrazione
può essere compreso
pensando che una fenditura
sufficientemente piccola
agisce come una sorgente di
onde sferiche.
L’ampiezza della fenditura determina l’ampiezza dell’immagine raccolta sullo
schermo posto oltre la fenditura.
Più stretta è la fenditura maggiore è l’ampiezza del massimo e minore è
l’intensità. Questo determina una perdita di risoluzione
Esperimento a doppia fenditura: interferenza
d
Una radiazione luminosa incide su uno
schermo in cui sono state praticate due
fenditure S1 e S2 poste a distanza d. Le
onde emergono da S1 e S2 in fase.
(a) Le onde incidenti nel punto P0 hanno
percorso lo stesso cammino ottico e
arrivano in fase (cresta su cresta, ventre
su ventre) e quindi interferiscono
costruttivamente sullo schermo
producendo una frangia luminosa
centrale.
(b) Le onde arrivano sfasate nel punto P’0
(cresta su ventre e viceversa) quindi
interferiscono distruttivamente
producendo una frangia scura.
(c) Le onde arrivano in fase in P1 e perciò
interferiscono costruttivamente.
Gli angoli qm che individuano i centri
delle frange chiare sono dati da:
dsenqm=±ml (m=0,1,2...)
l=532.4 nm
d=0.44mm
D= 230 cm
l=532.4 nm
d=0.8mm
D= 230 cm
d
D
Esperimento di interferenza da doppia
fenditura al variare della distanza tra le
fenditure e della lunghezza d’onda.
Nota la lunghezza d’onda, dalla distanza fra le
frange si risale alla distanza d fra le due
fenditure.
L’intensità del massimo centrale è modulata
dall’ampiezza delle fenditure che è costante in
questo esperimento
l=400 nm
d=0.8 mm
D=230 cm
Simile risultato si ha quando si ha un reticolo costituito da N
fenditure (o sorgenti puntiformi) poste a distanza d una
dall’altra.
Anche in questo caso le onde interferiscono costruttivamente
sullo schermo quando la differenza di cammino ottico dsenq è
pari a un numero intero di lunghezze d’onda.
dsenqm=±ml (m=0,1,2...)
Cristalli
I cristalli sono costituiti da atomi disposti in modo da formare una cella
elementare che si ripete all’infinito formando un reticolo regolare. Il passo di
tale reticolo è generalmente dell’ordine di qualche angstrom (1 Å= 10-10 m)
Esempio:cella elementare del NaCl
(sale da cucina) a0=5.63 Å
Na+
ClSe un cristallo è investito da una
radiazione di lunghezza d’onda
fissata, darà luogo al fenomeno di
diffrazione
da
reticolo
precedentemente descritta purchè la
lunghezza d‘onda sia comparabile con
il passo reticolare, ovvero l~1-10 Å
Reticolo cristallino del NaCl
Raggi X
I raggi X sono radiazione elettromagnetica con
lunghezza d’onda compresa tra 10-11 e 10-8 m. Sono
quindi la radiazione adatta per fare esperimenti di
diffrazione su reticoli cristallini
I raggi X possono essere prodotti mediante tubi a
raggi X oppure eccitando atomi i quali decadono
producendo radiazione elettromagnetica di
lunghezza d’onda fissate.
Per esempio il rame dà raggi X con l=1.54 nm
Esperimento di diffrazione su un cristallo di MgB2
Fissata la lunghezza d’onda incidente l=1.54 nm si osservano dei
massimi di intensità in corrispondenza di alcuni angoli.
Dalla posizione angolare
dei picchi si risale ai passi
reticolari del cristallo
tramite la relazione:
2dsenqm=ml (m=0,1,2...)
Il picco a 25.2°
corrisponde ad un valore
di a0=3.524 Å
25.2°
1000
500
21°
0
20
21
22
23
angolo
24
25
26
Diffrazione da un reticolo cristallino
In realtà in uno spettro di
diffrazione si osservano
molti picchi.
Questo è dovuto al fatto che
in un cristallo si possono
individuare diverse famiglie
di piani.
Ognuna di queste dà luogo
a un differente picco di
diffrazione.
angolo